基于Or-Tools的整数规划问题求解

Or-Tools官网整数规划问题
- - 导入线性求解器
  - 声明 MIP 求解器
  - 定义变量
  - 定义约束条件
  - 定义目标函数
  - 调用 MIP 求解器
  - 打印结果
  - 完整代码
Or-Tools官网例题:求解大规模问题的数组表示
- - 构造数据
  - 实例化求解器
  - 定义变量
  - 定义约束条件
  - 定义目标函数
  - 调用求解器
- - 完整代码

线性规划问题中，有些最优解可能是分数或小数，事实上，线性规划是连续变量的线性优化问题。但在实际中，常有要求解答必须是整数的情形（称为整数解）。例如，所求解是机器的台数、完成工作的人数或装货的车辆数等，分数或小数的解答就不合要求。为了满足整数解的要求，初看起来，似乎只要把已得到的带有分数或小数的解经过“舍入化整”就可以了。但这常常是不行的，因为化整后不见得是可行解；或虽是可行解，但不一定是最优解。因此，对求最优整数解的问题，有必要另行研究。我们称这样的问题为整数线性规划（integer linear programming），简称 ILP，整数线性规划是最近几十年来发展起来的数学规划论中的一个分支。

整数线性规划中如果所有的变量都限制为（非负）整数，就称为纯整数线性规划（pureinteger linear programming）或称为全整数线性规划（all integer linear programming）；如果仅一部分变量限制为整数，则称为混合整数线性规划（mixed integer linearprogramming）。整数线性规划的一种特殊情形是0—1规划，它的变量取值仅限于0或1。本章最后讲到的指派问题就是一个0—1规划问题。

Or-Tools官网整数规划问题

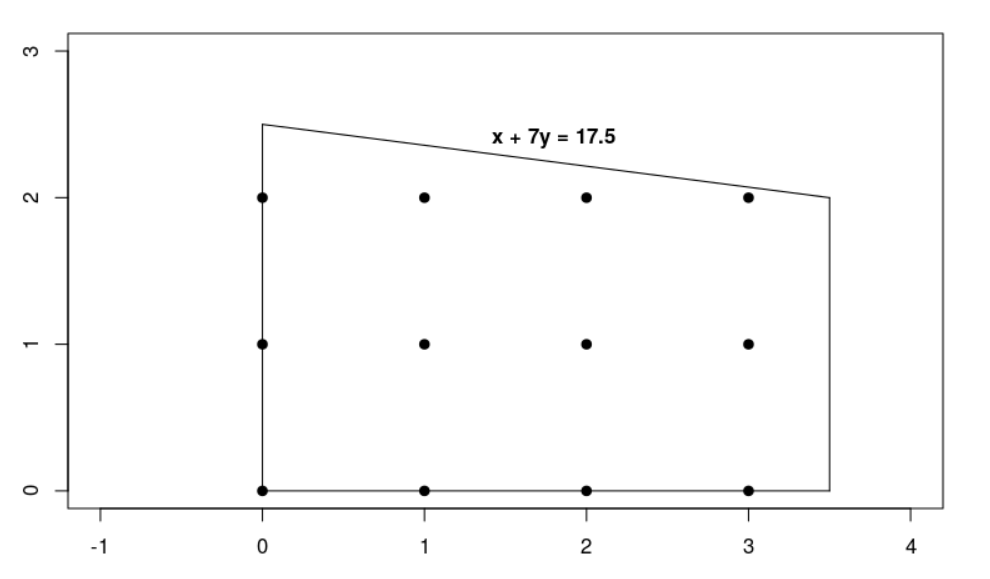
在遵循以下限制条件的情况下，x + 10y 最大化：

x + 7y ≤ 17.5
0 ≤ x ≤ 3.5
0 ≤ y
x、y 为整数
画出可行域如下图所示:

导入线性求解器

from ortools.linear_solver import pywraplp

声明 MIP 求解器

solver = pywraplp.Solver.CreateSolver("SAT")

定义变量

infinity = solver.infinity()
# x and y are integer non-negative variables.
x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")

print("Number of variables =", solver.NumVariables())

定义约束条件

# x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5)

# x <= 3.5.
solver.Add(x <= 3.5)

print("Number of constraints =", solver.NumConstraints())

定义目标函数

# Maximize x + 10 * y.
solver.Maximize(x + 10 * y)

调用 MIP 求解器

print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()

打印结果

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print("Objective value =", solver.Objective().Value())
    print("x =", x.solution_value())
    print("y =", y.solution_value())
else:
    print("The problem does not have an optimal solution.")

完整代码

from ortools.linear_solver import pywraplp


def main():
    # Create the mip solver with the SCIP backend.
    solver = pywraplp.Solver.CreateSolver("SAT")
    if not solver:
        return

    infinity = solver.infinity()
    # x and y are integer non-negative variables.
    x = solver.IntVar(0.0, infinity, "x")
    y = solver.IntVar(0.0, infinity, "y")

    print("Number of variables =", solver.NumVariables())

    # x + 7 * y <= 17.5.
    solver.Add(x + 7 * y <= 17.5)

    # x <= 3.5.
    solver.Add(x <= 3.5)

    print("Number of constraints =", solver.NumConstraints())

    # Maximize x + 10 * y.
    solver.Maximize(x + 10 * y)

    print(f"Solving with {solver.SolverVersion()}")
    status = solver.Solve()

    if status == pywraplp.Solver.OPTIMAL:
        print("Solution:")
        print("Objective value =", solver.Objective().Value())
        print("x =", x.solution_value())
        print("y =", y.solution_value())
    else:
        print("The problem does not have an optimal solution.")

    print("\nAdvanced usage:")
    print("Problem solved in %f milliseconds" % solver.wall_time())
    print("Problem solved in %d iterations" % solver.iterations())
    print("Problem solved in %d branch-and-bound nodes" % solver.nodes())


if __name__ == "__main__":
    main()

Or-Tools官网例题:求解大规模问题的数组表示

上面问题中, 采用如下语法一个一个定义变量

x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")

在大规模问题中变量较多, 用数组表示变量较为方便.
$\begin{matrix} \max 7x_1 + 8x_2 + 2x_3 + 9x_4 + 6x_5 \\ 5 x_1 + 7 x_2 + 9 x_3 + 2 x_4 + 1 x_5 \leq 250\\ 18 x_1 + 4 x_2 - 9 x_3 + 10 x_4 + 12 x_5 \leq 285\\ 4 x_1 + 7 x_2 + 3 x_3 + 8 x_4 + 5 x_5 \leq 211\\ 5 x_1 + 13 x_2 + 16 x_3 + 3 x_4 - 7 x_5 \leq 315 \end{matrix}$
其中 x1、x2、…、x5 为非负整数。

构造数据

 """Stores the data for the problem."""
    data = {}
    # 变量系数矩阵
    data["constraint_coeffs"] = [
        [5, 7, 9, 2, 1],
        [18, 4, -9, 10, 12],
        [4, 7, 3, 8, 5],
        [5, 13, 16, 3, -7],
    ]
    # 约束右端项
    data["bounds"] = [250, 285, 211, 315]
    # 目标函数系数
    data["obj_coeffs"] = [7, 8, 2, 9, 6]
    # 变量个数\维度
    data["num_vars"] = 5
    # 约束个数
    data["num_constraints"] = 4

实例化求解器

solver = pywraplp.Solver.CreateSolver("SCIP")

定义变量

infinity = solver.infinity()
x = {}
for j in range(data["num_vars"]):
    x[j] = solver.IntVar(0, infinity, "x[%i]" % j)
print("Number of variables =", solver.NumVariables())

定义约束条件

用 MakeRowConstraint 方法（或某些变体，具体取决于编码语言）创建约束条件。该方法的前两个参数是限制条件的下限和上限。第三个参数是约束名称（ str类型, 可选参数）。

for i in range(data["num_constraints"]):
	# 约束条件
    constraint = solver.RowConstraint(0, data["bounds"][i], "")
    for j in range(data["num_vars"]):
    	# 设置约束条件中每个变量的系数
        constraint.SetCoefficient(x[j], data["constraint_coeffs"][i][j])
print("Number of constraints =", solver.NumConstraints())

在Python中, 上面的还可以用如下方式表达:

for i in range(data['num_constraints']):
     constraint_expr = [data['constraint_coeffs'][i][j] * x[j] for j in range(data['num_vars'])]
     solver.Add(sum(constraint_expr) <= data['bounds'][i])

定义目标函数

objective = solver.Objective()
for j in range(data["num_vars"]):
    objective.SetCoefficient(x[j], data["obj_coeffs"][j])
objective.SetMaximization()
# In Python, you can also set the objective as follows.
# obj_expr = [data['obj_coeffs'][j] * x[j] for j in range(data['num_vars'])]
# solver.Maximize(solver.Sum(obj_expr))

调用求解器

status = solver.Solve()

/# 打印结果

if status == pywraplp.Solver.OPTIMAL:
    print("Objective value =", solver.Objective().Value())
    for j in range(data["num_vars"]):
        print(x[j].name(), " = ", x[j].solution_value())
    print()
    print("Problem solved in %f milliseconds" % solver.wall_time())
    print("Problem solved in %d iterations" % solver.iterations())
    print("Problem solved in %d branch-and-bound nodes" % solver.nodes())
else:
    print("The problem does not have an optimal solution.")

完整代码

from ortools.linear_solver import pywraplp


def create_data_model():
    """Stores the data for the problem."""
    data = {}
    data["constraint_coeffs"] = [
        [5, 7, 9, 2, 1],
        [18, 4, -9, 10, 12],
        [4, 7, 3, 8, 5],
        [5, 13, 16, 3, -7],
    ]
    data["bounds"] = [250, 285, 211, 315]
    data["obj_coeffs"] = [7, 8, 2, 9, 6]
    data["num_vars"] = 5
    data["num_constraints"] = 4
    return data



def main():
    data = create_data_model()
    # Create the mip solver with the SCIP backend.
    solver = pywraplp.Solver.CreateSolver("SCIP")
    if not solver:
        return

    infinity = solver.infinity()
    x = {}
    for j in range(data["num_vars"]):
        x[j] = solver.IntVar(0, infinity, "x[%i]" % j)
    print("Number of variables =", solver.NumVariables())

    for i in range(data["num_constraints"]):
        constraint = solver.RowConstraint(0, data["bounds"][i], "")
        for j in range(data["num_vars"]):
            constraint.SetCoefficient(x[j], data["constraint_coeffs"][i][j])
    print("Number of constraints =", solver.NumConstraints())
    # In Python, you can also set the constraints as follows.
    # for i in range(data['num_constraints']):
    #  constraint_expr = \
    # [data['constraint_coeffs'][i][j] * x[j] for j in range(data['num_vars'])]
    #  solver.Add(sum(constraint_expr) <= data['bounds'][i])

    objective = solver.Objective()
    for j in range(data["num_vars"]):
        objective.SetCoefficient(x[j], data["obj_coeffs"][j])
    objective.SetMaximization()
    # In Python, you can also set the objective as follows.
    # obj_expr = [data['obj_coeffs'][j] * x[j] for j in range(data['num_vars'])]
    # solver.Maximize(solver.Sum(obj_expr))

    status = solver.Solve()

    if status == pywraplp.Solver.OPTIMAL:
        print("Objective value =", solver.Objective().Value())
        for j in range(data["num_vars"]):
            print(x[j].name(), " = ", x[j].solution_value())
        print()
        print("Problem solved in %f milliseconds" % solver.wall_time())
        print("Problem solved in %d iterations" % solver.iterations())
        print("Problem solved in %d branch-and-bound nodes" % solver.nodes())
    else:
        print("The problem does not have an optimal solution.")


if __name__ == "__main__":
    main()