基于WIN10的64位系统演示

一、写在前面

这一期，我们介绍基于ARIMA的组合模型。

（1）数据源：

《PLoS One》2015年一篇题目为《Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic Fever with Renal Syndrome in Jiangsu Province, China》文章的公开数据做演示。数据为江苏省2004年1月至2012年12月肾综合症出血热月发病率。运用2004年1月至2011年12月的数据预测2012年12个月的发病率数据。

（2）组合策略：

（a）在SCI论文中，单纯的ARIMA模型一般是用来作为基线的，因为它最经典，也最稳定。在此基础上，组合上其他模型，理论上有可能会提高模型的预测效能。其中的逻辑主要在于，ARIMA模型只能捕获线性信息，而可能还存在的非线性信息则需要借助其他非线性模型进行进一步的提取和利用。

（b）常用的组合策略包括：

（b1）ARIMA-GRNN组合模型：这个是最最经典的组合模型的策略。首先，构建ARIMA模型，得出训练集的拟合序列F和预测序列Y；其次，从拟合序列F中随机挑选2个数值，构建GRNN模型（还记得GRNN模型的参数只有一个光滑因子不？因此只需要2个数值即可）；最后，使用构建的GRNN模型对ARIMA的拟合序列F和预测序列Y进行再次预测，结果即为ARIMA-GRNN组合模型的最终预测结果。

（b2）矫正残差策略：首先，构建ARIMA模型，得出训练集的拟合序列F和预测序列Y；其次，分别计算出训练集和验证集的残差序列X_S和X_Y，使用第二种时间序列模型基于残差序列X_S进行建模，预测得出训练集和验证集的残差序列X_S#和X_Y#；最后，将X_S与X_S#相加，得到组合模型的最终拟合序列，同理，将Y_S与Y_S#相加，得到组合模型的最终预测序列。

二、组合模型实战

（1）单纯ARIMA预测

为了方便演示，我直接使用JMP软件来做演示。采用2004年1月至2011年12月的数据作为训练集建立ARIMA（1,1,1）(0,0,1)12模型，预测2012年1月至12月的发病率。

训练集的拟合数据、验证集的预测数据如下：

稍微算一下MAE得了：

训练集的MAE：0.013076

验证集的MAE：0.013059

（2）ARIMA-GRNN组合模型：

祭出我封装的Matlab小程序：

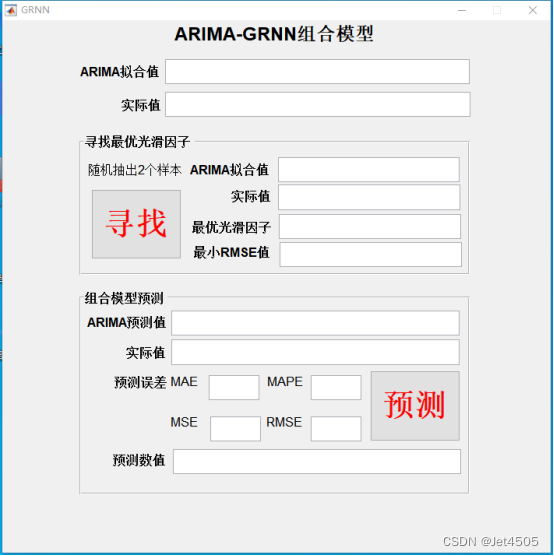
（a）插入说明书：

1.界面

1.1 ARIMA拟合值 输入由ARIMA模型所取得的拟合值。

1.2实际值 输入与ARIMA拟合值对应的实际值。

1.3 寻找最优光滑因子界面

1.3.1 ARIMA拟合值 输出随机抽样的2个样本的ARIMA拟合值。

1.3.2 实际值 输出随机抽样的2个样本的实际值，与ARIMA拟合值对应。

1.3.3 最优光滑因子 输出最优光滑因子。

1.3.4 最小RMSE值 输出在最优光滑因子下模型的预测误差（RMSE值）。

1.3.5 寻找 点击后输出以上四个数值，并以图表显示光滑因子从0.001到5（步长为0.001）模型的预测误差（RMSE值）。

1.4 组合模型预测界面

1.4.1 ARIMA预测值 输入ARIMA预测值。

1.4.2 实际值 输入实际值。注意，如果是为了认证模型精度，则输入对应的实际值；如果是用于预测，则全部填0，个数必须与ARIMA预测值一致。此时下面的预测精度没有参考意义。

1.4.2 预测误差 MAE 输出模型拟合的平均绝对误差；

               MAPE 输出模型拟合的平均相对误差；

               MSE 输出模型拟合的均方误差；

               RMSE 输出模型拟合的均方根误差。

1.4.3 预测 点击后输出预测误差，并以图表显示预测值与实际值的曲线图。

（b）实战：

2.1 输入ARIMA拟合值和实际值，点击寻找；

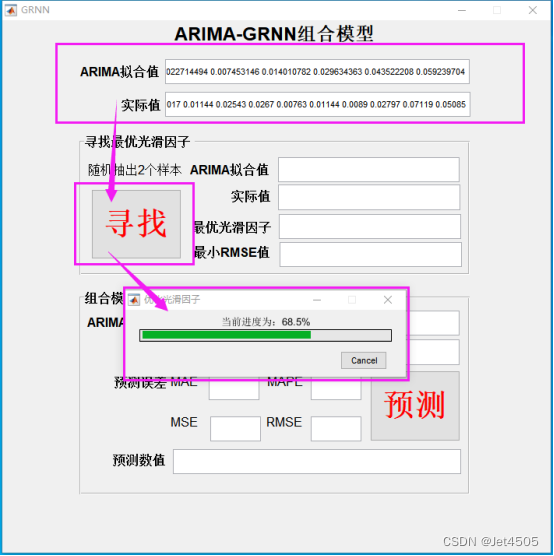
2.2 输出随机抽取的2对ARIMA拟合值以及对应的实际值，最优光滑因子以及最小RMSE值。并以图表显示光滑因子从0.001到5（步长为0.001）模型的预测误差（RMSE值）；

2.3 输入ARIMA预测值以及对应的实际值，这里我们是在认证模型精度，故实际值已知，如图。若用于预测，则实际值是不知道的，需填入12个0（不展示）；

2.4 点击预测，输出预测误差，并以图表显示预测值与实际值的曲线图，如图。若用于预测，则输出的预测误差没有参考意义（不展示）；

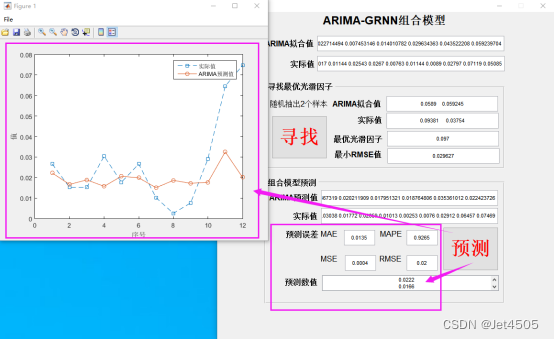
看看组合前后验证集的MAE：

前：0.013059；

后：0.0135

没啥变化，甚至还提升了，大型翻车现场，哈哈哈。所以，组合模型不是万能的。

（3）矫正残差策略：

这个策略，我们就拿着ARIMA的拟合残差序列使劲薅。

就试一试随机森林吧，用单步滚动预测：

得出预测的残差序列，如下：

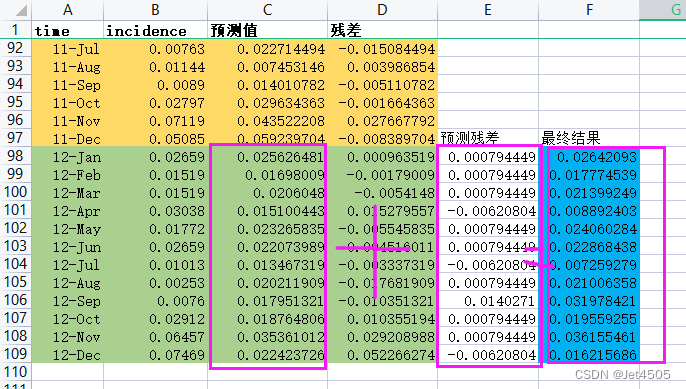
看看组合前后验证集的MAE：

前：0.013059；

后：0.015223

甚至还变差了，继续大型翻车现场。

其余模型就不尝试了，思路就是那么一个思路，大家尽情发挥。

三、写在后面

组合模型不是万能的，还得看数据，因地制宜！！！

四、数据

链接：https://pan.baidu.com/s/1r32fnMI69LgfxEWa7MHt9w?pwd=62uh

提取码：62uh