代碼隨想錄算法訓練營|第四十九天|139.单词拆分、关于多重背包、背包问题总结。刷题心得（c++）

news2024/9/23 11:18:00

讀題

139.单词拆分

自己看到题目的第一想法

看完代码随想录之后的想法

139.单词拆分 - 實作

思路

Code

關於多重背包

與01背包與完全背包的差別

轉化成01背包問題

背包问题总结

背包問題分類

背包問題 - 遞推公式

最多裝多少/能否裝滿

最大價值

裝滿背包有多少方式

最少裝多少/能否裝滿

遍歷順序差異

01背包

完全背包

總結

自己实现过程中遇到哪些困难

今日收获，记录一下自己的学习时长

相關資料

讀題

139.单词拆分

自己看到题目的第一想法

看到的當下有點矇，不知道該怎麼去解，我要如何去做?

誰是背包誰是物品也沒有搞清楚，直接看題解。

看完代码随想录之后的想法

單詞就是物品，字符串s就是背包，單詞能否組成字符串，可以想成物品能不能把背包裝滿

拆分的過程中，可以重複單詞，就表示這不是01背包問題，而是完全背包問題

因為遍歷物品的時候，子字符串都是從j = 0 開始，所以不用擔心dp[i] 之間的如果都是false

因為dp[0] = 1 這是構成這套方式可以成功執行的關鍵之一

139.单词拆分 - 實作

思路

定義DP數組以及下標的含意

dp[i]: 字符串長度i，如果dp[i] 為true，代表有一個或多個字典元素所組成。
遞推公式

如果dp[j] (可以想成子字符串的起點) 為true，代表之前的數值是由一個或多個字典元素所組成。

所以如果[j - i] 也就是j 到 i 的區間子串有出現在字典元素當中，代表dp[i] 也為true

遞推公式為: if([j, i] == word_Dict && dp[j] == true) dp[i] = true;
根據遞推公式，確定DP數組如何初始化

dp[0] = true, 可以想成沒有任何字串的狀況下，有一種方法可以組成字符串長度為0，會比較好理解。
確定遍歷順序

在字符串長度遍歷的過程中，比如說’aba’ 字典裡有a, b

雖然aab 也是字符串有的元素，只是排列不同但aab ≠ aba

所以我們求的是排列，需要先遍歷背包在遍歷物品

Code

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(), wordDict.end()); //建立wordDict 讓後續程式可以快速查找
        vector<bool> dp(s.size() + 1, false);
        dp[0] = true;

        for(int i = 0; i <= s.size(); i++) {
            for(int j = 0; j < i; j++) {
                string word = s.substr(j, i - j); //[j,i] 的子串
                if(wordSet.find(word) != wordSet.end() && dp[j]) {
                    dp[i] = true;
                }
            }
        }
        return dp[s.size()];
    }
};

關於多重背包

與01背包與完全背包的差別

01 背包: 物品有兩個維度的資料: 價值、重量，數量則只能有一個

完全背包: 物品有兩個維度的資料: 價值、重量，數量則有無限個，可以重複取相同物品

多重背包: 物品變為有三個維度的資料: 價值、重量、數量，並且可以重複取

跟01背包有點像，將數量展開，其實就是01背包，一樣是取與不取，只是數據上有許多相同物品

跟完全背包也有點像，因為可以重複取相同的物品，只是數量有限

轉化成01背包問題

其實在剛剛提到多重背包可以轉化成01背包

在代碼隨想錄中有相關的code，主要轉化的過程如下

vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    vector<int> nums = {2, 3, 2};
    int bagWeight = 10;
    for (int i = 0; i < nums.size(); i++) {
        while (nums[i] > 1) { // nums[i]保留到1，把其他物品都展开
            weight.push_back(weight[i]);
            value.push_back(value[i]);
            nums[i]--;
        }
    }

透過展開物品，讓問題轉化成01背包問題

或者透過多加一層嵌套的迴圈，也就是遍歷物品時，將數量全部都跑過一次

for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            // 以上为01背包，然后加一个遍历个数
            for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
                dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
            }
        }
        // 打印一下dp数组
        for (int j = 0; j <= bagWeight; j++) {
            cout << dp[j] << " ";
        }
        cout << endl;
    }

背包问题总结

背包問題分類

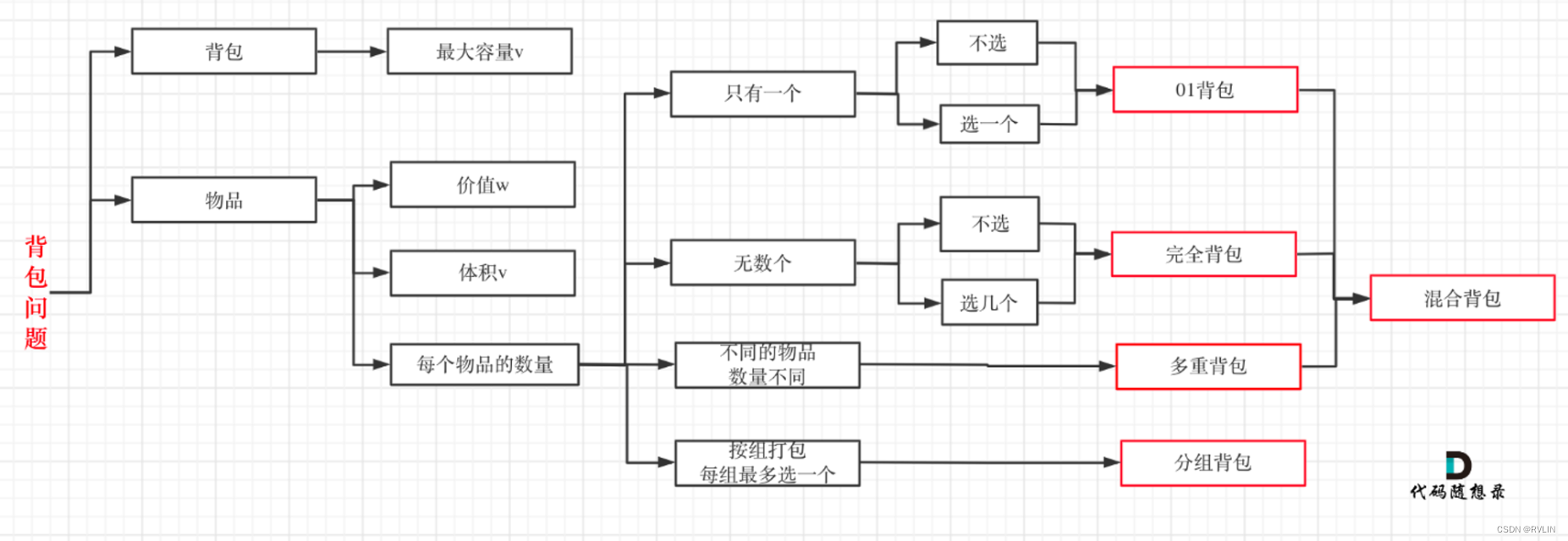
背包問題 - 遞推公式

最多裝多少/能否裝滿

dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); → 可以想像成物品重量與價值相等

對應題目

动态规划：416.分割等和子集(opens new window)
动态规划：1049.最后一块石头的重量 II

最大價值

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); → 可以想像成物品重量與價值不相等

對應題目

动态规划：474.一和零

裝滿背包有多少方式

dp[j] += dp[j - nums[i]];

對應題目

动态规划：494.目标和(opens new window)
动态规划：518. 零钱兑换 II(opens new window)
动态规划：377.组合总和Ⅳ(opens new window)
动态规划：70. 爬楼梯进阶版（完全背包）

最少裝多少/能否裝滿

dp[j] = min(dp[j - coins[i]] + 1, dp[j])

對應題目

动态规划：322.零钱兑换(opens new window)
动态规划：279.完全平方数

遍歷順序差異

01背包

二維dp

因為數值都會根據左上方以及正上方的值進行更新，所以當我們初始化第一行與第一列時，不管是從背包開始遞推還是物品開始遞推，都可以。

第二層遍歷順序是由小到大
一維dp

在二维數組中，每一層的數值都是當前位置的正上方以及左上方的數據得出

從二维壓縮成一维數組，我們需要模擬二维數組的方式

所以根據我們的遞推公式，我們不能使用正序遍歷，不然原本在二维數組中左上方的數據就會被覆蓋掉

而使用倒序可以保證每一層的數據都是由二维數組上一層正上方以及左上方得出的。
二維dp 滾動dp

在**动态规划：474.一和零中是有兩個維度的背包**

先遍歷物品，在遍歷二維背包

因為是滾動數組，所以二維背包是由後往前遍歷