工作中会不会经常会碰到一些数据指标的计算,比如百分比转化,保留几位小数等,就会出现计算不准确,数据精度丢失的情况。通过这篇分享借助第三方库能够轻松解决数据精度丢失的问题。
一、场景复现
JS数字精度丢失的一些常见问题
// 加法 =====================
0.1 + 0.2 === 0.3 // false
0.1 + 0.2 = 0.30000000000000004
0.7 + 0.1 = 0.7999999999999999
0.2 + 0.4 = 0.6000000000000001
// 减法 =====================
1.5 - 1.2 = 0.30000000000000004
0.3 - 0.2 = 0.09999999999999998
// 乘法 =====================
19.9 * 100 = 1989.9999999999998
0.8 * 3 = 2.4000000000000004
35.41 * 100 = 3540.9999999999995
// 除法 =====================
0.3 / 0.1 = 2.9999999999999996
0.69 / 10 = 0.06899999999999999为什么0.1 + 0.2 === 0.3是false呢?
先看下面这个比喻
比如一个数 1÷3=0.33333333......
3会一直无限循环,数学可以表示,但是计算机要存储,方便下次取出来再使用,但0.333333...... 这个数无限循环,再大的内存它也存不下,所以不能存储一个相对于数学来说的值,只能存储一个近似值,当计算机存储后再取出时就会出现精度丢失问题。
再看js里保留小数位tofixed()对于小数最后一位为5时进位不正确的问题
1.35.toFixed(1) // 1.4 正确
1.335.toFixed(2) // 1.33 错误
1.3335.toFixed(3) // 1.333 错误
1.33335.toFixed(4) // 1.3334 正确
1.333335.toFixed(5) // 1.33333 错误
1.3333335.toFixed(6) // 1.333333 错误可以看到,小数点位数为2,5时四舍五入是正确的,其它是错误。
根本原因还是计算机里浮点数精度丢失的问题
如:1.005.toFixed(2) 返回的是 1.00 而不是 1.01。
原因: 1.005 实际对应的数字是 1.00499999999999989,在四舍五入时全部被舍去。
1.005.toPrecision(21) //1.00499999999999989342二、浮点数
“浮点数”是一种表示数字的标准,整数也可以用浮点数的格式来存储,我们也可以理解成,浮点数就是小数,
在JavaScript中,现在主流的数值类型是Number,而Number采用的是IEEE754规范中64位双精度浮点数编码,
这样的存储结构优点是可以归一化处理整数和小数,节省存储空间。
对于一个整数,可以很轻易转化成十进制或者二进制。但是对于一个浮点数来说,因为小数点的存在,小数点的位置不是固定的。解决思路就是使用科学计数法,这样小数点位置就固定了。
而计算机只能用二进制(0或1)表示,二进制转换为科学记数法的公式如下:
其中,a的值为0或者1,e为小数点移动的位置。
举个例子:
27.0转化成二进制为11011.0 ,科学计数法表示为:
![]()
其中,a的值为0或者1,e为小数点移动的位置。
举个例子:
27.0转化成二进制为11011.0 ,科学计数法表示为:
![]()
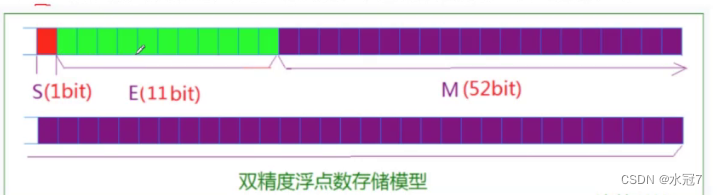
前面讲到,javaScript存储方式是双精度浮点数,其长度为8个字节,即64位比特,
64位比特又可分为三个部分:
符号位S:第 1 位是正负数符号位(sign),0代表正数,1代表负数;
指数位E:中间的 11 位存储指数(exponent),用来表示次方数,可以为正负数。在双精度浮点数中,指数的固定偏移量为1023;
尾数位M:最后的 52 位是尾数(mantissa),超出的部分自动进一舍零;
如下图所示:

举个例子:
27.5 转换为二进制11011.1
11011.1转换为科学记数法 [公式]
符号位为1(正数),指数位为4+,1023+4,即1027
因为它是十进制的需要转换为二进制,即 10000000011,小数部分为10111,补够52位即: 1011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000`
所以27.5存储为计算机的二进制标准形式(符号位+指数位+小数部分 (阶数)),既下面所示:
0+10000000011+011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000`
二、问题分析
再回到问题上
0.1 + 0.2 === 0.3 // false
0.1 + 0.2 = 0.30000000000000004通过上面的学习,我们知道,在javascript语言中,0.1 和 0.2 都需要先将十进制转化成二进制后再进行运算。
// 0.1 和 0.2 都转化成二进制后再进行运算
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111
// 转成十进制正好是 0.30000000000000004所以输出false
再来一个问题,那么为什么x=0.1得到0.1?
主要是存储二进制时小数点的偏移量最大为52位,最多可以表达的位数是2^53=9007199254740992,对应科学计数尾数是 9.007199254740992,这也是 JS 最多能表示的精度。
它的长度是 16,所以可以使用 toPrecision(16) 来做精度运算,超过的精度会自动做凑整处理。
.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000,去掉末尾的零后正好为 0.1但看到的 0.1 实际上并不是 0.1。不信你可用更高的精度试试:
0.1.toPrecision(21) = 0.100000000000000005551小结
计算机存储双精度浮点数需要先把十进制数转换为二进制的科学记数法的形式,然后计算机以自己的规则{符号位+(指数位+指数偏移量的二进制)+小数部分}存储二进制的科学记数法。
因为存储时有位数限制(64位),并且某些十进制的浮点数在转换为二进制数时会出现无限循环,会造成二进制的舍入操作(0舍1入),当再转换为十进制时就造成了计算误差。
三、解决方案
理论上用有限的空间来存储无限的小数是不可能保证精确的,但我们可以处理一下得到我们期望的结果。
当你拿到 1.4000000000000001 这样的数据要展示时,建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示,如下:
parseFloat(1.4000000000000001.toPrecision(12)) === 1.4 // True封装成方法就是:
function strip(num, precision = 12) {
return +parseFloat(num.toPrecision(precision));
}对于运算类操作,如 +-*/,就不能使用 toPrecision 了。正确的做法是把小数转成整数后再运算(先扩大再缩小法)。
以加法为例:
/**
* 精确加法
*/
function add(num1, num2) {
const num1Digits = (num1.toString().split('.')[1] || '').length;
const num2Digits = (num2.toString().split('.')[1] || '').length;
const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
return (num1 * baseNum + num2 * baseNum) / baseNum;
}以toFixed()为例
//先扩大再缩小法
function toFixed(num, s) {
var times = Math.pow(10, s)
// 0.5 为了舍入
var des = num * times + 0.5
// 去除小数
des = parseInt(des, 10) / times
return des + ''
}
console.log(toFixed(1.333332, 5))最后还可以使用第三方库,如Math.js、BigDecimal.js
参考文献
- 数值-阮一峰
- BigInt - JavaScript | MDN