数据的表示和运算:
进位计数制:
对于我们现在使用的如十进制计数法,二进制计数法等,符号反映权重,比如十进制的0~9,9这个符号的权重和0是不一样的,而且现在的计数法符号所在位置也反映权重,比如个位上的1 和十位上的 1 的权重也是不一样的。
计算机组成原理中的"位权"通常指的是二进制数中每个位所代表的数值大小或权重。在二进制表示中,每个位的权值是2的幂次方,从右到左依次递增,通常从0开始。这意味着最右边的位的权值为2^0,接下来一位的权值为2^1,再下一位的权值为2^2,依此类推。r进制的位权也是类似意思。
基数:每个数码位所用到的不同符号的个数,r进制的基数就是r,比如10进制的基数是10个,0~9,二进制是2个,0~1.
计算机使用二进制的原因在于:
1、 可使用两个稳定状态的物理器件表示;
2、 0,1正好对应逻辑值 假、真 ,方柏霓实现逻辑运算;
3、 可很方便地使用逻辑门电路实现算术运算。
二、八、十六进制的相互转换:
二进制 -> 八进制 ,从最低位(小数点前最低位,小数点后最高位)起,每三位一组,每组转换成对应的八进制符号,高位不足补0.
比如二进制的 1 111 000 010 . 011 010 -> 1 7 0 2 . 3 2
八进制 -> 二进制 ,每位八进制转化成对应的 3位二进制
二进制与十六进制的转换也是这个这样的,不过是四对一,这个转换还蛮好用的。
各种进制的常见书写方式:
二进制 : (10001)₂ 100001B ,这个B可以表示二进制,自己不知道,注意点,下面的H,D都是一样的,记住。
八进制:(12347)₈
十六进制:(14ABCDEF)₁₆ 1652H (16进制:hexadecimal) 0x1652(这个是零,不是o,记住记住)
十进制:(1689)₁₀ 1897D (10机制:decimalism)
这里还有十进制转化成其他进制,不多赘述。
BCD码:用二进制编码的十进制
8421码:8421码就是用四位的二进制一一对应表示十进制的 0~9,四位的二进制码权值从高到低就是 8 4 2 1嘛,0000表示0,0001表示1,0010表示2,以此类推,不过这种表示方式 1010~1111是没有定义的,没有对应的值,而且这样如果十进制的 5+8=13 ,对应到8421码上是
0101 + 1000 =1101,这个1101是不再映射表里面的,处理方法就是对这种不再映射表的值再加 0110 (强制向高位进1),然后得到的值就是十进制对应的二进制结果,如 1101 + 0110 = 1 0011,就是 13 。
然后还有 余3码:就是再8421码的基础上再加上3 ,比如原本 0000对应的 0,现在是0011对应0;
还有 2421码:2421码是改变了权值的定义 ,现在这四位二进制的权值分别是 2 4 2 1,4以下,包括4,对应值关系和8421码是一样的,比如4 还是 0100,但4以上的值就定义保证最高位的2为1,这样是为了避免歧义,比如5可以表示为 0101,也可以表示为 1011,但有了最高位的要求,就只能是 1011,这样就避免歧义的发生。也就是说对于2421码,表示 0~4 的时候最高位是 0,表示 5~9的时候最高位是 1.
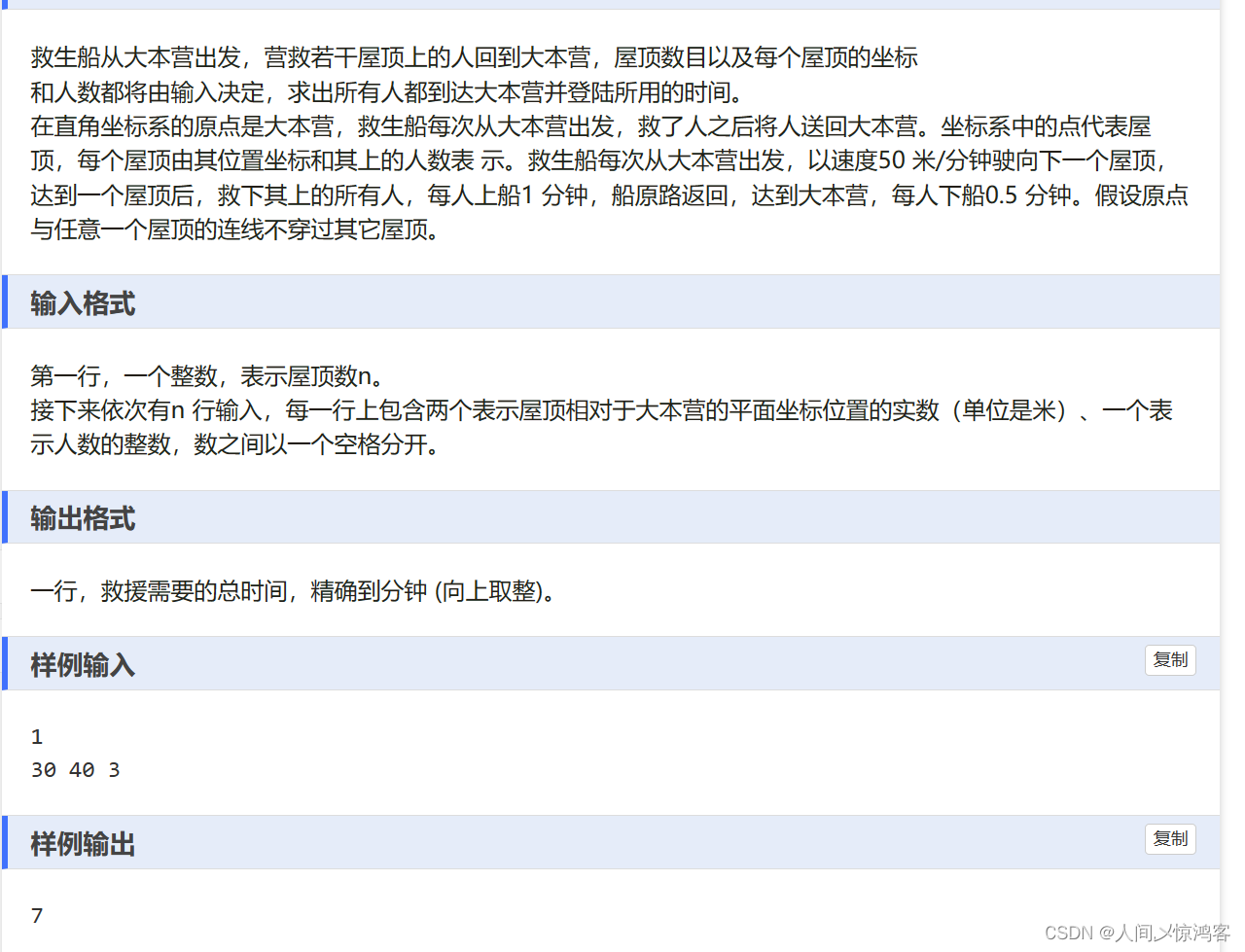
这个题,可以用ceil函数实现向上取整,不过我感觉写的这个没有用ceil函数的也挺好玩的。其实主要是我学c的时候还真没有学到ceil函数,就不知道。
向上取整是指,不小于该值的最小整数,例如 1.2的是2,-2.3的是-2
向下取整是指,不大于该值的最大整数。
#include<math.h>
int main()
{
int n = 0;
scanf("%d", &n);
float x = 0.;
float y = 0.;
int num = 0;
int i = 0;
float sum = 0.;
for (i = 0; i < n; i++)
{
scanf("%f %f %d", &x, &y, &num);
sum += sqrt(x * x + y * y) / 50*2 + num * 1.5;
}
if(sum-(int)sum==0)//这个地方
printf("%d", (int)sum);
else
printf("%d", (int)sum+1);
return 0;
}这个是ceil函数,向上取整。
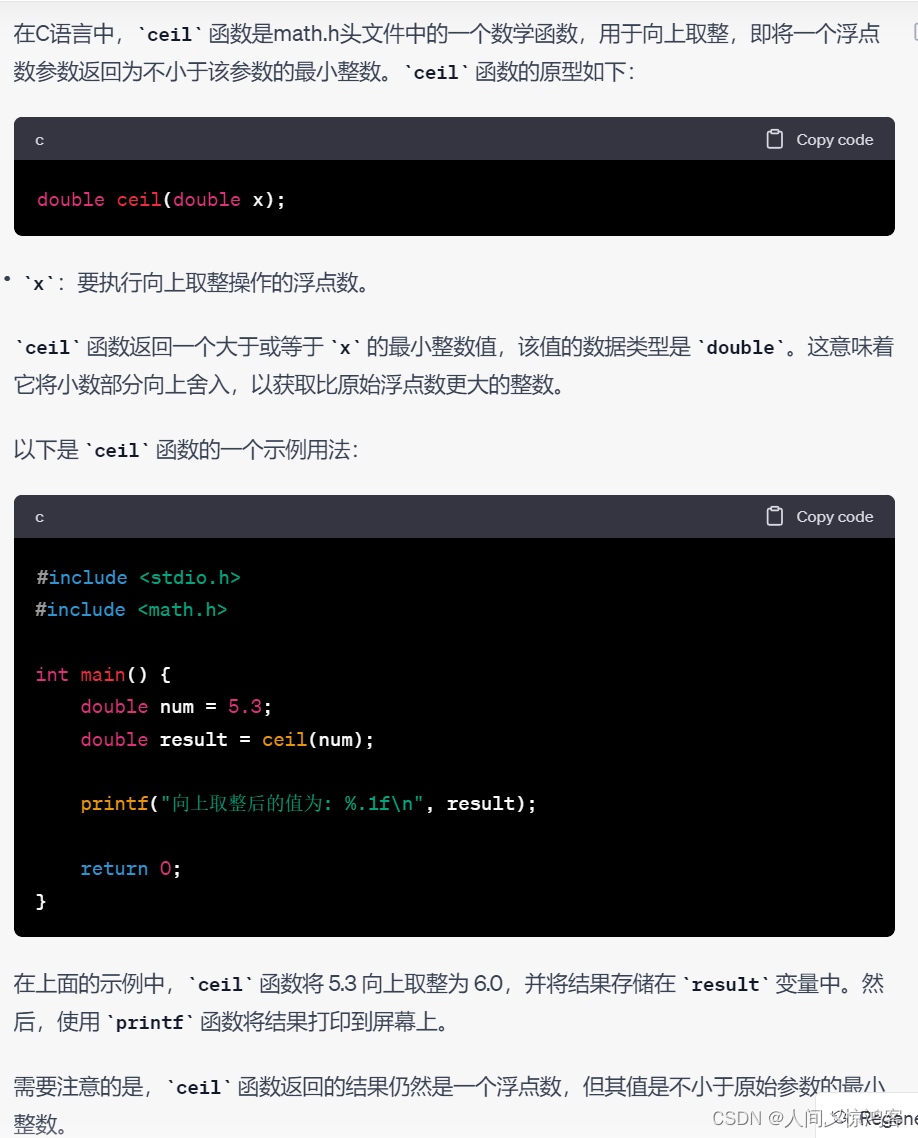
然后还有向下取整函数floor,一起先简单学了吧
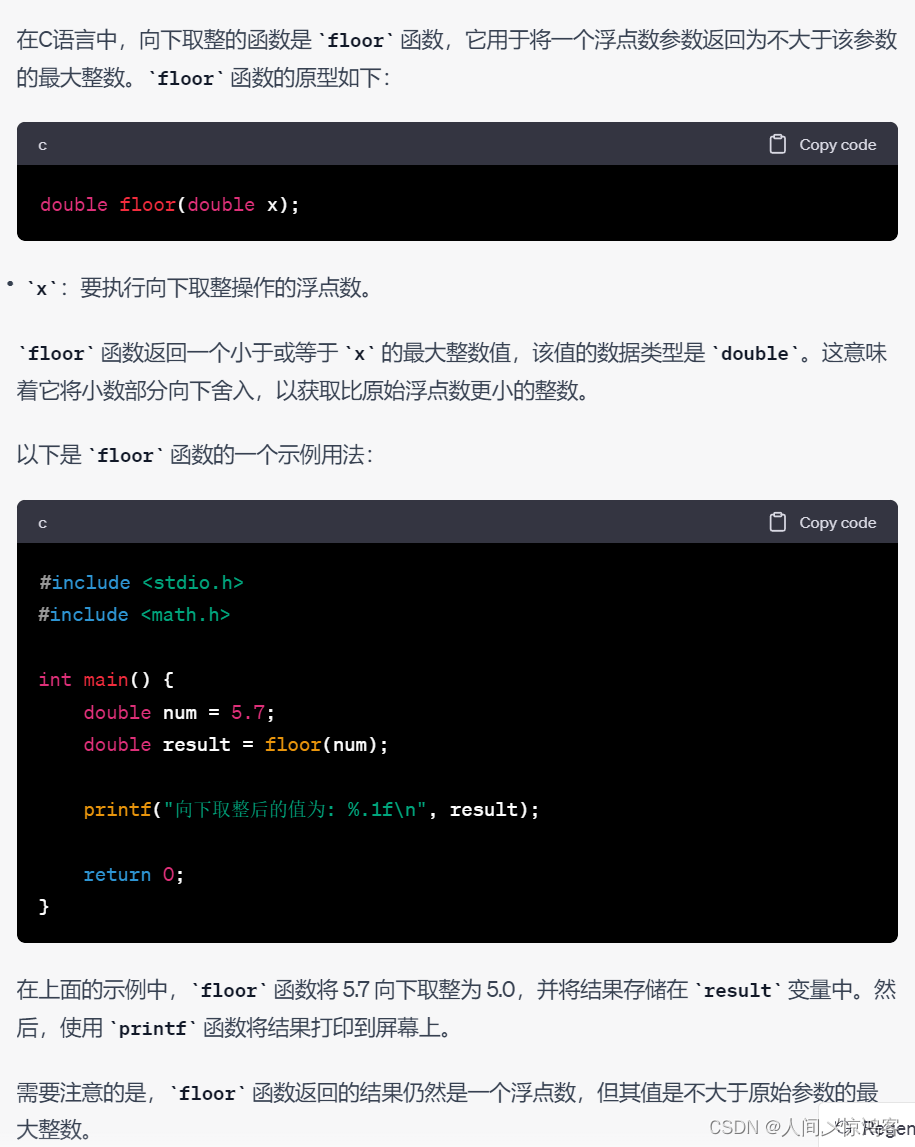
这个地方注意一点 : n*=3+1;效果和n*=4;一样,不是先乘三再加一;这里我输入的是3,
好了刚刚又发现了一个错误,!的级别比%要高,所以应该这样写!(n%2)