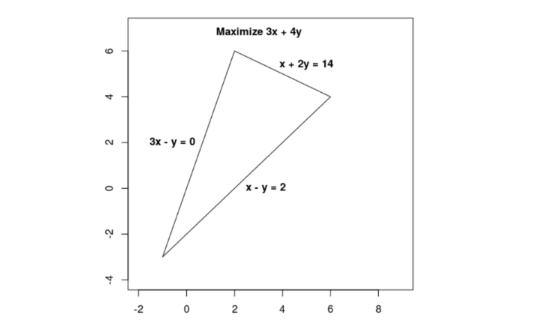
画出可行域如图所示：

Python调用ortools求解

导入求解器

# 导入(或包含)or - tools线性求解器包装器，这是MIP求解器和线性求解器的接口，如下所示
from ortools.linear_solver import pywraplp

声明线性规划求解器

MPsolver is a wrapper for several different solvers, including Glop. The code below declares the GLOP solver.

solver = pywraplp.Solver.CreateSolver("GLOP")

创建决策变量

x = solver.NumVar(0, solver.infinity(), "x")
y = solver.NumVar(0, solver.infinity(), "y")
f"Number of variables ={solver.NumVariables()}"

'Number of variables =2'

约束条件

# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)
# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)
# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)

print("Number of constraints =", solver.NumConstraints())

定义目标函数

# Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y)

调用求解器

status = solver.Solve()

### 打印结果

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print("Objective value =", solver.Objective().Value())
    print("x =", x.solution_value())
    print("y =", y.solution_value())
else:
    print("The problem does not have an optimal solution.")

Solution:
Objective value = 0.0
x = 0.0
y = 0.0

Java调用ortools求解

package org.example;

import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

/**
 * Simple linear programming example.
 */
public final class LinearProgrammingExample {
    public static void main(String[] args) {
        Loader.loadNativeLibraries();
        MPSolver solver = MPSolver.createSolver("GLOP");

        double infinity = java.lang.Double.POSITIVE_INFINITY;
        // x and y are continuous non-negative variables.
        MPVariable x = solver.makeNumVar(0.0, infinity, "x");
        MPVariable y = solver.makeNumVar(0.0, infinity, "y");
        System.out.println("Number of variables = " + solver.numVariables());

        // x + 2*y <= 14.
        MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
        c0.setCoefficient(x, 1);
        c0.setCoefficient(y, 2);

        // 3*x - y >= 0.
        MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
        c1.setCoefficient(x, 3);
        c1.setCoefficient(y, -1);

        // x - y <= 2.
        MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
        c2.setCoefficient(x, 1);
        c2.setCoefficient(y, -1);
        System.out.println("Number of constraints = " + solver.numConstraints());

        // Maximize 3 * x + 4 * y.
        MPObjective objective = solver.objective();
        objective.setCoefficient(x, 3);
        objective.setCoefficient(y, 4);
        objective.setMaximization();

        final MPSolver.ResultStatus resultStatus = solver.solve();

        if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
            System.out.println("Solution:");
            System.out.println("Objective value = " + objective.value());
            System.out.println("x = " + x.solutionValue());
            System.out.println("y = " + y.solutionValue());
        } else {
            System.err.println("The problem does not have an optimal solution!");
        }

        System.out.println("\nAdvanced usage:");
        System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");//运行时间
        System.out.println("Problem solved in " + solver.iterations() + " iterations");//迭代次数
    }

    private LinearProgrammingExample() {
    }
}