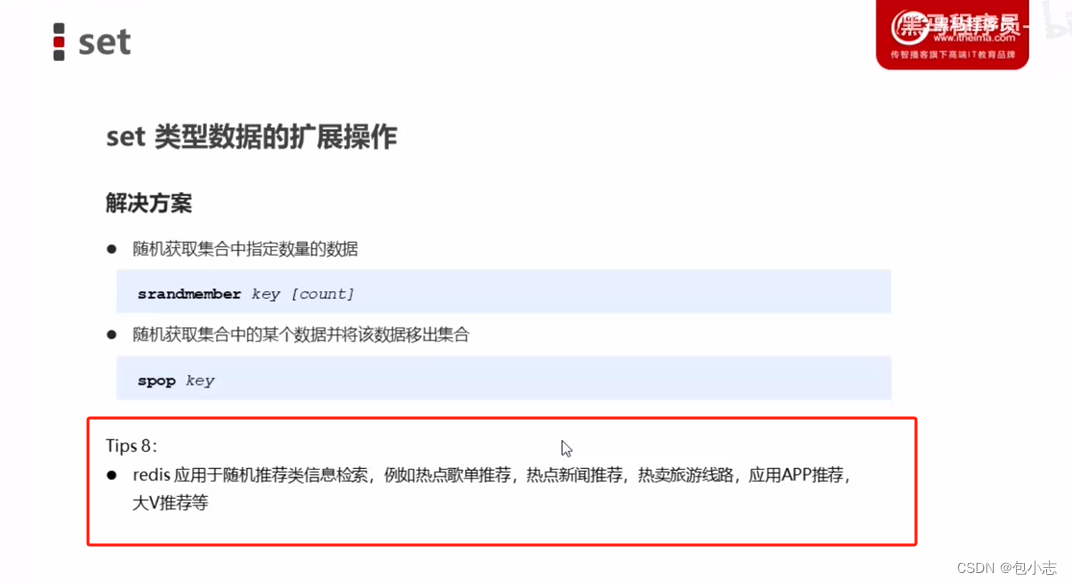
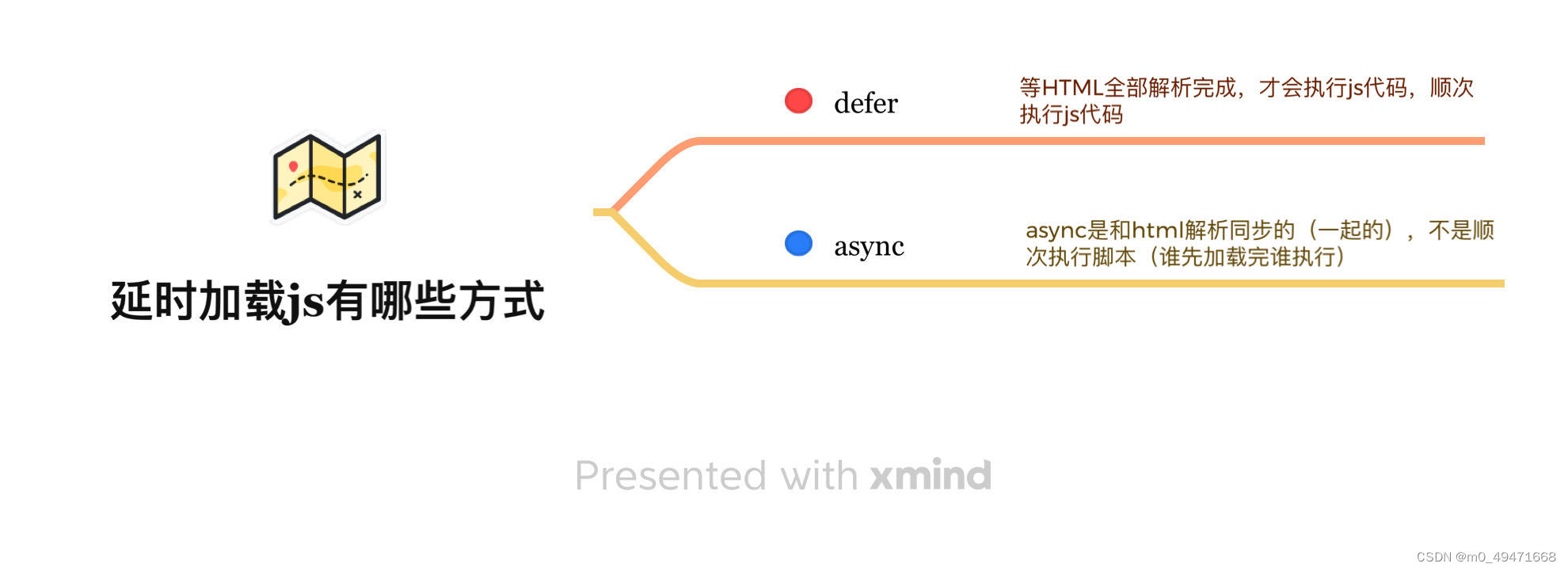
问题描述: 
上述题目的意思为,人工造出一些数据点,对我们的模型y = Xw + b + ∈进行训练,其中标准模型如下:
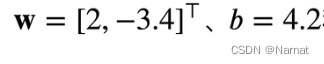
其中W和X都为张量,我们训练的模型越接近题目给出的标准模型越好
训练过程如下:
人造数据集:
说人话,自己利用代码随机创造一些有规律的点,组成点集类似这样:
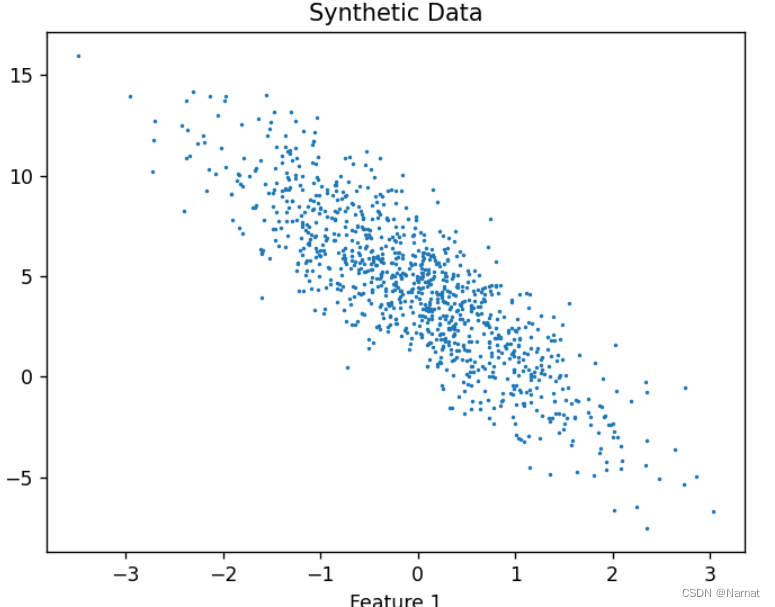
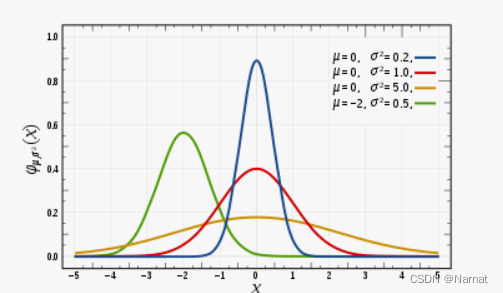
上述点集就服从正态分布:
正态分布(也被称为高斯分布)是统计学中最常见的概率分布之一。它具有以下特征:
1、均值(Mean):正态分布具有一个均值,通常表示为 μ(mu),它代表分布的中心或平均值。分布的对称轴就是均值。
2、方差(Variance):正态分布的方差,通常表示为 σ^2(sigma
squared),代表数据点分散或离散程度的度量。方差越大,数据点越分散。3、随机性:正态分布中的随机变量的值可以取任何实数值,但大多数值集中在均值周围,远离均值的值出现的概率逐渐减小。正态分布的概率密度函数呈钟形曲线,这个曲线是对称的。
正态分布的概率密度函数通常由以下公式表示:
正态分布概率密度函数4、 正态分布在自然界和科学研究中经常出现,许多现象,如身高、体重、温度测量误差等,都可以近似地用正态分布来描述。正态分布在统计学、机器学习和数据分析中广泛应用,因为它具有许多有用的性质,包括中心极限定理等。
正态分布的特征使得它在各种应用中非常有用,包括假设检验、参数估计、回归分析等。
生成y点实现函数:
下列函数用途是带入真实的w, b再根据随机的x真实的y
这一作用是为了构造人工点集,等会训练模型用
def synthetic_data(w, b, num_examples):
"""生成 Y = XW + b + 噪声。"""
X = torch.normal(0, 1, (num_examples, len(w)))# 均值为0,方差为1的随机数,n个样本,列数为w的长度
y = torch.matmul(X, w) + b # y = x * w + b
c = torch.normal(0, 0.01, y.shape)
y += c # 加入随机噪音,均值为0.。形状与y的一样
return X, y.reshape((-1, 1))# x, y做成列向量返回
最后返回的x, y就是点了
简单的张量运算:
根据矩阵乘法规则,要使这两个矩阵相乘,第一个矩阵的列数必须等于第二个矩阵的行数。
例如:
张量 [[1, 2], [3, 4]] 和张量 [1, 2]可以进行矩阵乘法:
前者一行两列,后者两行两列可乘:
[1*1 + 2*2, 3*1+ 4*2] = [5, 11]
反过来就不成乘了,两者shape分别是(1, 2), (2,)可兼容
张量和向量的区别:
朴素又简单的说,张量能表示任意维度,而向量是一维:
也就是说[1, 2]既可以表示为行向量也可以表示为一行两列的张量
[[1],[2]]这个也既可以表示为列向量或者两行一列的张量
再其他的都是张量了,张量的范围更广泛
代码的拆解分析:
X = torch.normal(0, 1, (num_examples, len(w)))# 均值为0,方差为1的随机
这个是为了更好的与w相乘,最后结果自然与上上述的例子一样,最后得到一个行向量
y.reshape((-1, 1))
作用:
y.reshape((-1, 1)) 是将张量 y 重新塑造(reshape)为一个列向量的操作。这里的 -1 是一个特殊的值,它表示自动计算该维度的大小以保持其他维度的元素数量不变。
假设原始的张量 y 是一个一维行向量,形状为 [n],其中 n 表示元素的数量。通过 y.reshape((-1, 1))
操作,你将其转换为一个列向量,形状为 [n, 1],其中 n 仍然表示元素的数量,但现在它们按列排列,而不是按行排列。这种操作通常在深度学习和线性代数中用于将数据从一种形状转换为另一种形状,以适应模型的需求。列向量通常用于表示目标值或标签,而行向量通常用于表示特征。通过这种方式,你可以确保数据的形状与模型的期望输入/输出形状相匹配。
数据打乱批量返还函数:
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))#转成list
random.shuffle(indices)#打乱
for i in range(0, num_examples, batch_size):#
batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])#取
yield features[batch_indices], labels[batch_indices]#不断返回
这个函数的作用主要就是将上述生成的一堆点,打乱,批量返还,方便下述数据处理,训练模型
代码的拆解分析:
num_examples = len(features)
indices = list(range(num_examples))#转成list
获取features长度,方便后续利用索引取值
batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])#取
indices[i:min(i + batch_size, num_examples)//切片取值
切片取值:
例如:
original_list = [0, 1, 2, 3, 4]
sliced_list = original_list[1:3] # 得到 [1, 2]
yield features[batch_indices], labels[batch_indices]#不断返回,y整理形状的用途就体现出来了
索引取值:
若二维张量a = [[0, 1, 2, 3, 4], [0, 1, 2, 3, 4]]
那么a[[0, 1]]:
a[[0, 1]] 表示对二维张量 a 进行行的索引操作,同时获取第 0 行和第 1 行的元素子集。它返回的是一个包含所选择的行的新的二维张量,其中包含了多个元素。
例如:
a = torch.tensor([[1, 2],
[3, 4],
[5, 6],
[7, 8],
[9, 10]])
那么:
a[[1, 3, 4]就是:
tensor([[3, 4],
[7, 8],
[9, 10]])
yield可以迭代返还,不像retrurn只返回一次,后续会在模型学习里继续补充
计算y值函数:
主要作用就是对我们的模型进行计算,我们的模型的有效值就是w,b它带入上述产生的x得到Y,这个Y是我们的模型计算出来的
def linreg(x, w, b):
return torch.matmul(x, w) + b
代价函数:
def squared_loss(y_hat, y):
return (y_hat - y.reshape(y_hat.shape))**2 / 2 / batch_size
梯度下降篇章讲的很详细不再赘述
梯度下降函数:
def sgd(params, lr, batch_size):
"""小批量随梯度下降"""
with torch.no_grad():#节省内存和计算资源。
for param in params:
param -= lr * param.grad
param.grad.zero_()#用于清空张量param的梯度信息。
详情:深度学习_5_模型拟合_梯度下降原理
同上不再赘述
主函数:
true_w = torch.tensor([2, -3.4])
true_b = 4.2#真正的答案
features, labels = synthetic_data(true_w, true_b, 100)#产生的数据集|点集
batch_size = 10#每次取的数据量
#模型
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad = True)
lr = 0.03 #学习率
num_ecopchs = 30 #数据扫描三遍
net = linreg #指定模型
loss = squared_loss #损失
for epoch in range(num_ecopchs):#扫描数据
for x, y in data_iter(batch_size, features, labels): #拿出x, y
l = loss(net(x, w, b), y)#求损失,预测net,真实y
l.sum().backward()#算梯度
sgd([w, b], lr, batch_size)#使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
#print(train_l)
print(f'epoch {epoch + 1},loss {float(train_l.mean()):f}')
#print(f'W {w}, B {b}')
拆解理解:
true_w = torch.tensor([2, -3.4])
true_b = 4.2#真正的答案
features, labels = synthetic_data(true_w, true_b, 100)#产生的数据集|点集
上述代码为了产生数据用来训练模型
#模型
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad = True)#b是[0]
上述代码为我们的模型w是均值为0方差为0.001的随机数,
注意一下这里生成的模型w和上述true_w的维度可就不同了,这里w的shape是(2, 1)产生的张量案例为[[1], [2]]
与模型相乘的x还与上述一致(batch_size,2)
由于x的列数为2,w的行数为2相同,所以两者仍然可相乘!且最后生成(batch_size, 1)的二维张量
汗流浃背了吧?
上运行结果:
求真实y: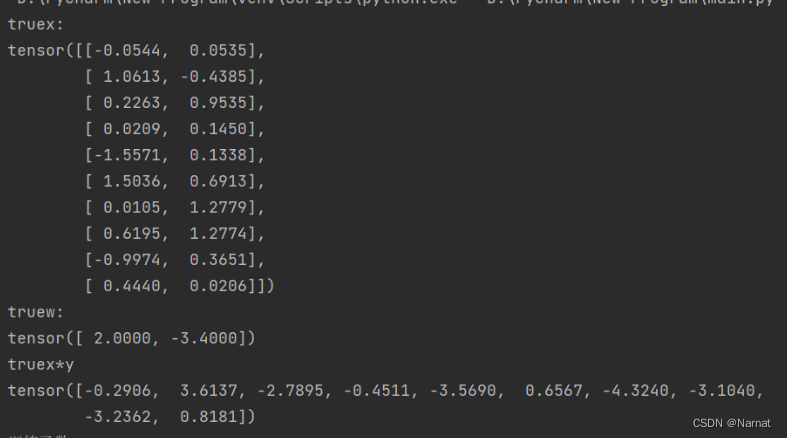
上述三个张量分别为:x, true_w, true_y
求模型y:
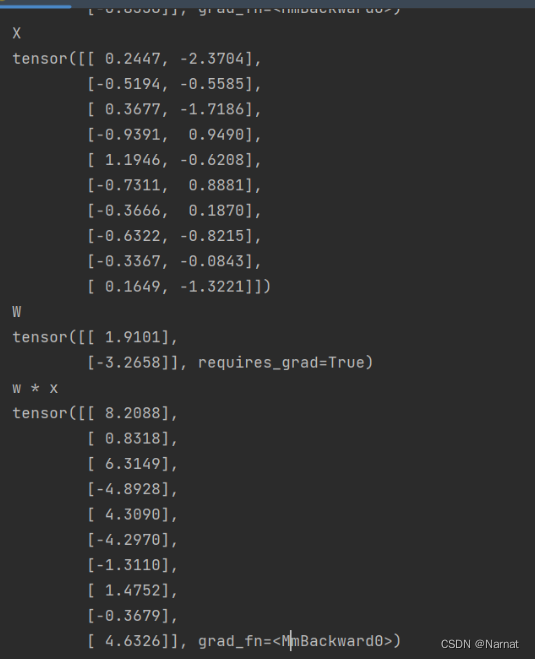
上述三个张量分别为X, w, X*w
lr = 0.03 #学习率
num_ecopchs = 30 #数据扫描三遍
net = linreg #指定模型
loss = squared_loss #损失
下述循环执行三十次,也就是对整个数据循环学习三十次
for epoch in range(num_ecopchs):#扫描数据
因为学习率0.03大小适中,学习次数在[1, 30]随次数增加,模型w会越来越接近true_w,学习次数再多起来,可能就会产生无效学习浪费时间,当然学习率也要适中,详情可看上篇博客
net = linreg #指定模型
loss = squared_loss #损失
上述俩语句只是为了方便后续更改模型,所以直接调用模型名字
for x, y in data_iter(batch_size, features, labels): #拿出x, y
l = loss(net(x, w, b), y)#求损失,预测net,真实y
l.sum().backward()#算梯度
sgd([w, b], lr, batch_size)#使用参数的梯度更新参数
此for循环配合data_iter函数内的yield语句可以把整个点集合分批次取出,实质是for循环调用了迭代器,此for循环是否结束和data_iter函数内的for循环相关
l.sum().backward()#算梯度
至于为什么要求和算梯度,这就是上篇博客梯度下降原理的作用了
requires_grad=True
上述代码标记了,某个变量在后续梯度计算中会用到,系统会跟踪,至于具体是用求偏导,还是别的算法,就不是我们该管的了,计算机帮你求
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
#print(train_l)
print(f'epoch {epoch + 1},loss {float(train_l.mean()):f}')
#print(f'W {w}, B {b}')
==下列语句是,就是不让进行梯度跟踪 ==
with torch.no_grad():
因为就是想打印一下模型训练结果
train_l = loss(net(features, w, b), labels)
上述代码,测试一下测试好的模型的损失值
print(f'epoch {epoch + 1},loss {float(train_l.mean()):f}')
打印格式,打印训练次数,与损失值
train_l.mean()
平均损失值
以上全部代码细节分析完毕
完整代码:
import random
import torch
def synthetic_data(w, b, num_examples):
"""生成 Y = XW + b + 噪声。"""
X = torch.normal(0, 1, (num_examples, len(w)))# 均值为0,方差为1的随机数,n个样本,列数为w的长度
y = torch.matmul(X, w) + b # y = x * w + b
c = torch.normal(0, 0.01, y.shape)
y += c # 加入随机噪音,均值为0.。形状与y的一样
return X, y.reshape((-1, 1))# x, y做成列向量返回
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))#转成list
random.shuffle(indices)#打乱
for i in range(0, num_examples, batch_size):#
batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])#取
yield features[batch_indices], labels[batch_indices]#不断返回
def linreg(x, w, b):
return torch.matmul(x, w) + b
def squared_loss(y_hat, y):
return (y_hat - y.reshape(y_hat.shape))**2 / 2 / batch_size
def sgd(params, lr, batch_size):
"""小批量随梯度下降"""
with torch.no_grad():#节省内存和计算资源。
for param in params:
param -= lr * param.grad
param.grad.zero_()#用于清空张量param的梯度信息。
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 100)
batch_size = 10
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad = True)
lr = 0.03 #学习率
num_ecopchs = 30 #数据扫描三遍
net = linreg #指定模型
loss = squared_loss #损失
for epoch in range(num_ecopchs):#扫描数据
for x, y in data_iter(batch_size, features, labels): #拿出x, y
l = loss(net(x, w, b), y)#求损失,预测net,真实y
l.sum().backward()#算梯度
sgd([w, b], lr, batch_size)#使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1},loss {float(train_l.mean()):f}')
#print(f'W {w}, B {b}')
运行效果:

可以看出随着学习次数的增加,误差也在逐渐减小
如果还觉得抽象,可以是输出我们训练的模型w和b
效果:
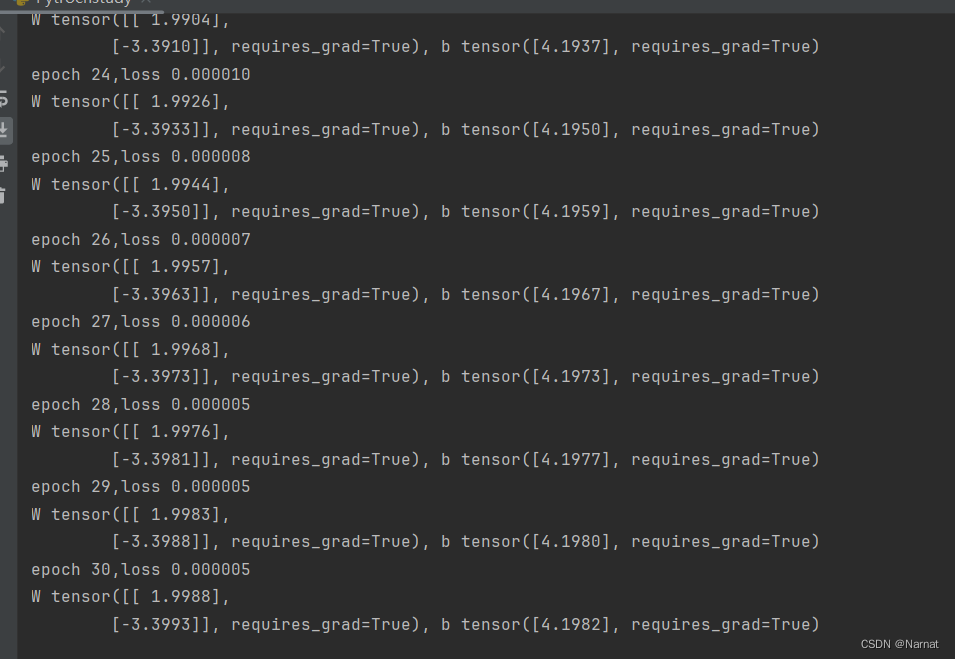
可以看出随着训练的次数增加我们训练的模型w与b和标准答案也越加趋近
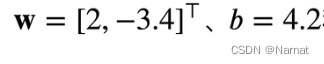
到此完结梯度下降原理博客如下:
深度学习_5_模型拟合_梯度下降原理