一、一阶低通滤波的原理

式子中的α作为滤波系数，X ( n ) 为本次的采样值，Y ( n − 1 ) 为上次滤波的输出值，Y ( n ) 为本次滤波后的输出值

一阶低通滤波器是一种常用的信号处理算法，用于去除高频噪声和平滑信号。其基本原理是通过对输入信号进行加权平均来减小高频分量。

具体而言，一阶低通滤波器可以表示为：

y[n] = (1 - α) * y[n-1] + α * x[n]

其中，x[n] 是输入信号的当前样本值，y[n] 是输出信号的当前样本值，α 是滤波器的时间常数，决定了滤波器的截止频率。

在实际应用中，时间常数 α 的选择非常关键，它决定了滤波器的响应速度和截止频率。一般来说，时间常数越小，滤波器响应速度越快，但截止频率也越高，因此会有更多高频分量通过滤波器。相反，时间常数越大，滤波器响应速度越慢，但截止频率也越低，因此能够更好地去除高频噪声。

需要注意的是，在使用一阶低通滤波器时，需要根据具体应用场景选择合适的时间常数，以达到最优的滤波效果。同时，由于该滤波器只考虑了前一时刻的输出值，因此对于快速变化的信号，可能会出现较大的误差。在这种情况下，可以考虑使用更高阶的滤波器或其他信号处理算法来优化滤波效果。

 二、Simulink仿真实现

1、整体工程

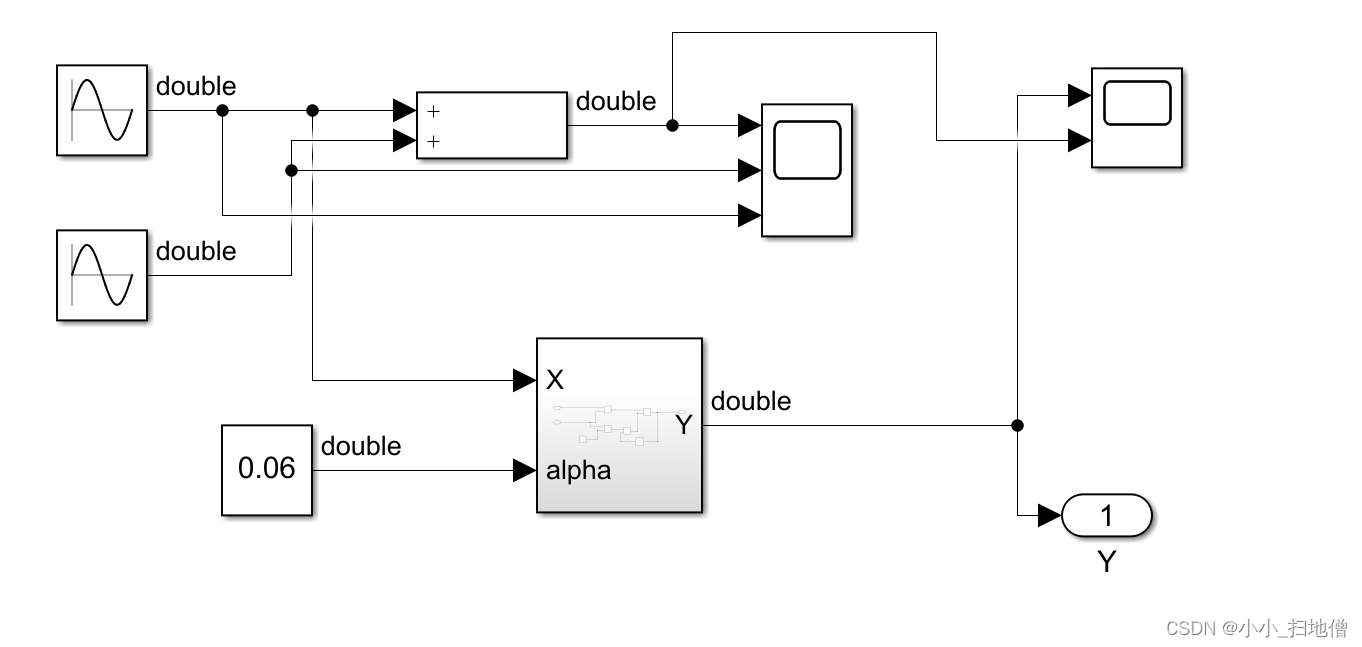
2、系统内工程 （算法实现部分）

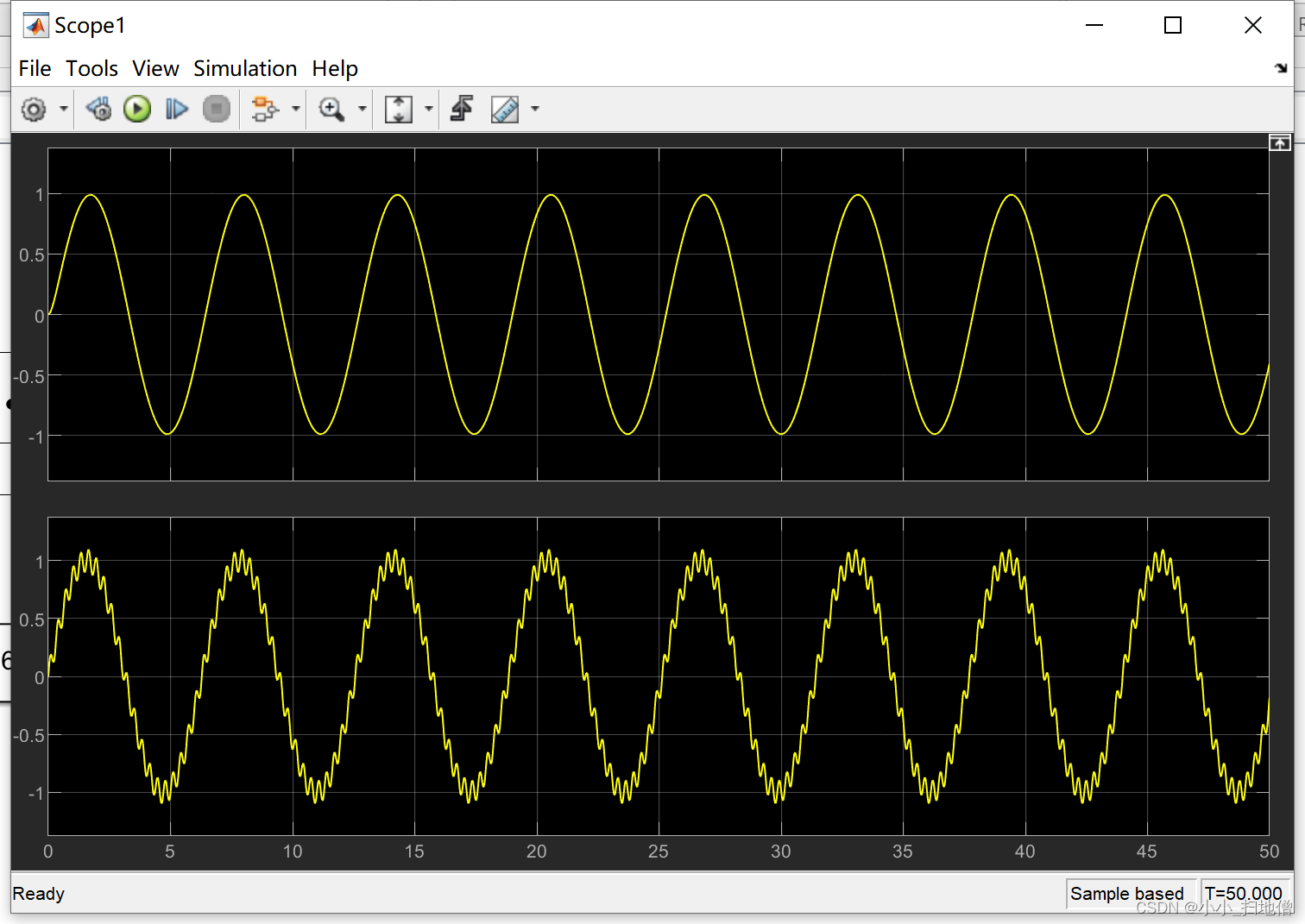
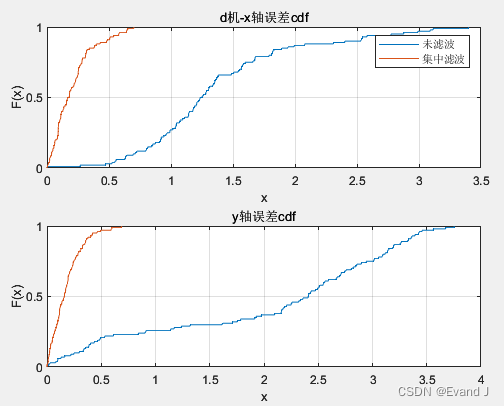
3、实现效果