1、题目

问题描述

过年小蓝想要回家串门。

蓝桥村可以抽象为 $n$ 个节点，$n-1$ 条边的一棵树，每条边有边权长度 $w_i$。

小蓝可以选择任意一个点作为起点，然后选择一条路径，可以访问每个节点至少一次。他想知道最短的路径长度是多少。

输入格式

第一行输入一个整数 $n$，表示节点数量。

接下来 $n-1$ 行，每行三个整数 $v_i,u_i,w_i$，表示 $(v_i,u_i)$ 存在一条 $w_i$ 的边。

输出格式

输出一个整数，表示最短路径。

样例输入

4
1 2 3
1 3 4
1 4 5

样例输出

15

说明

路径为：4->1->2->1->3，即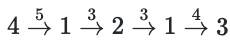，路径和值为 15。

数据范围

• $1\le n\le 10^5$
• $1\le v_i,u_i\le n$
• $1\le w_i\le 10^9$
• 保证数据输入是一棵树

原题链接

串门

2、思路

考察图论，树的性质。

由于每个点需要访问至少一次，我们可以选择任意点作为起点和终点，考虑枚举起点和终点，然后在满足起点终点的情况下访问每个节点至少一次的最短路。

结合dfs回溯的知识和欧拉路的知识可以得到一个结论。

1. 从起点到终点的最短路上的边，只需要经过一次。
2. 其他边，都需要至少两次。

利用容斥，假设每条边都需要访问两次，那么减去只访问一次的，就是结果。

所以实际上就是求树的直径。

用两遍DFS 或者 换根DP 都行。

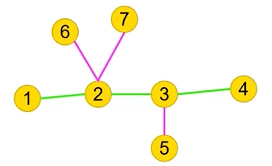
如上图示例，为了从起点1 到 终点 4，进行深搜，点6,7和5 的边都要走两次，如2到6之后要从6返回2，然后才能继续往下走，其他边都走一次。从1->2->3->4 就是最长的一条路径，也就是树的直径。除了直径，其他的边都要访问两次。

时间复杂度：$O(n)$

3、代码

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <assert.h>

using namespace std;

typedef long long ll;
const int N = 1e5+100;
const int MOD = 998244353;

typedef pair<int, int> Pair;

vector<Pair> G[N];
int n;
ll ans = 0;

ll dfs(int u, int f) {
    vector<ll> tw(0);
    for (Pair v : G[u]) {
        if (v.first == f) continue;
        ll t = dfs(v.first, u) + v.second;
        tw.push_back(t);
    }
    sort(tw.begin(), tw.end());
    int sz = tw.size();
    if (sz > 0)
        ans = max(ans, tw[sz - 1]);
    if (sz > 1)
        ans = max(ans, tw[sz - 1] + tw[sz - 2]);
    ll t = 0;
    if (sz > 0) t = tw[sz - 1];
    return t;
}

void sol() {
    int v, u, w;
    cin >> n;
    ll res = 0;
    for (int i = 1; i < n; ++i) {
        cin >> v >> u >> w;
        G[v].push_back({u, w});
        G[u].push_back({v, w});
        res += w;
    }
    res *= 2;
    dfs(1, 0);
    cout << res - ans << endl;
}

int main() {
    sol();
    exit(0);
}

或

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <assert.h>

using namespace std;

typedef long long ll;
const int N = 1e5+100;
const int MOD = 998244353;

typedef pair<int, int> Pair;

vector<Pair> G[N];
int n;
ll ans = 0;
ll tg;

void dfs(int u, int f, ll dep) {
    if (dep > ans) {
        ans = dep;
        tg = u;
    }
    for (Pair v : G[u]) {
        if (v.first == f) continue;
        dfs(v.first, u, dep + v.second);
    }
}

void sol() {
    int v, u, w;
    cin >> n;
    ll res = 0;
    for (int i = 1; i < n; ++i) {
        cin >> v >> u >> w;
        G[v].push_back({u, w});
        G[u].push_back({v, w});
        res += w;
    }
    res *= 2;
    dfs(1, 0, 0);
    ans = 0;
    dfs(tg, 0, 0);
    cout << res - ans << '\n';
}

int main() {
    sol();
    exit(0);
}