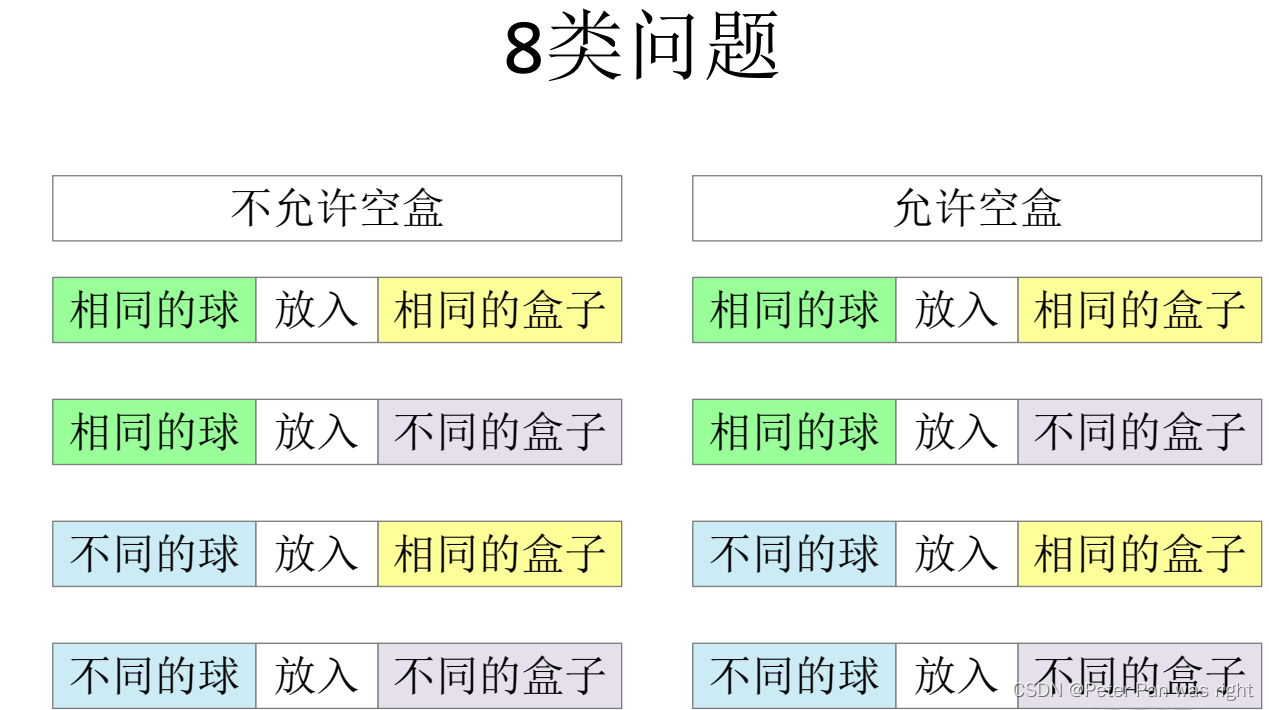
球盒问题有8类，分别如下图

相同的球放入相同的盒子

根据上一篇Peter算法小课堂—正整数拆分-CSDN博客

简单来说，就这样👇 

将相同的球放入相同的盒子，其实相当于将正整数i分为j个正整数的个数

cin>>n>>m;
if(n<m){
	cout<<0<<endl;
	return 0;
}
for(ll i=2;i<=n;i++) f[i][1]=1;
for(ll j=2;j<=m;j++)
	for(ll i=j;i<=n;i++)
		f[i][j]=f[i-1][j-1]+f[i-j][j];
cout<<f[n][n]<<endl;

相同的球放入不同的盒子

其实，我们直接排列组合一下

以每个盒子至少一个球举例。我们将这些球排成一排，用一些板把它们分开。如下图

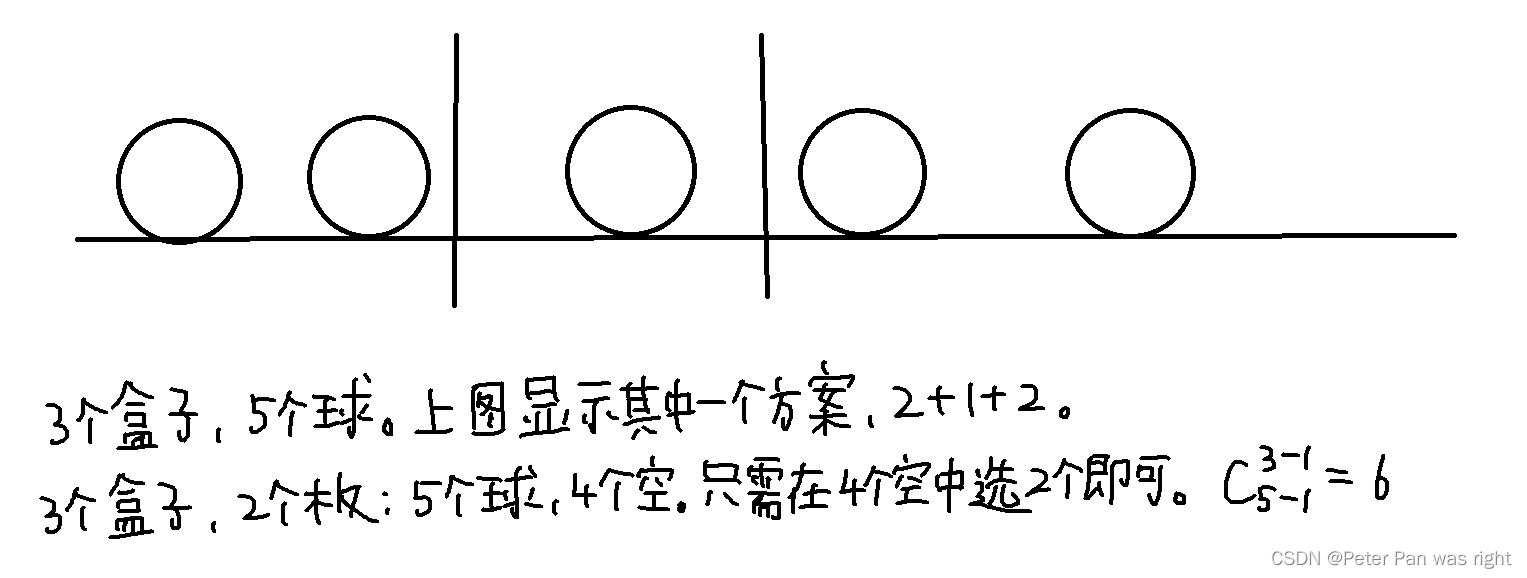
若每个盒子可为空，则我们可以在每个盒子里提前放一个球，其它同上。

cin>>n>>m;
if(n<m){
	cout<<0<<endl;
	return 0;
}
ll ans=1;
for(ll i=1;i<=m-1;i++){
	ans*=n-i;
	ans/=i;
}
cout<<ans<<endl;

不同的球放入相同的盒子（第二类stirling数）

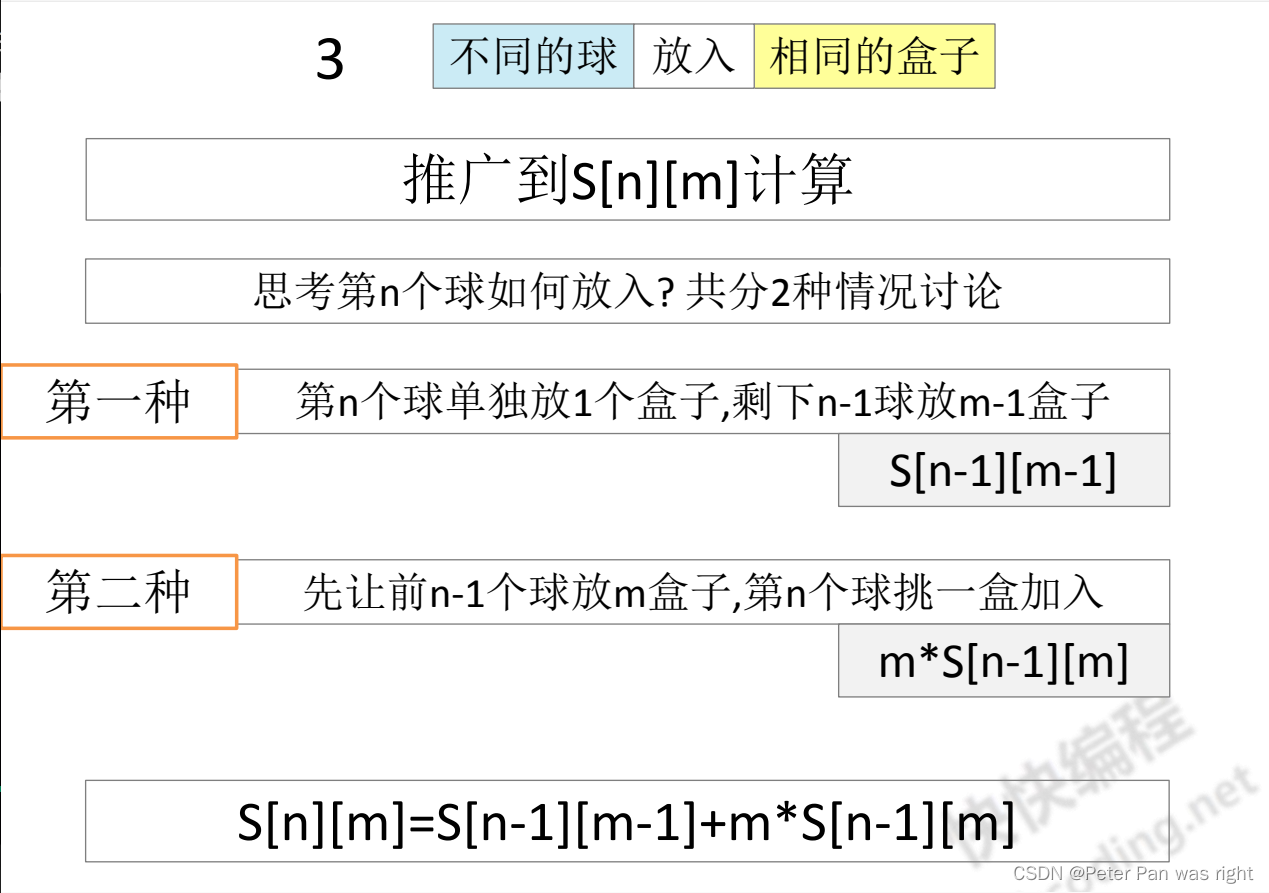
f[i][j]表示将前i个球放入相同的盒子，不允许空的情况，具体状态转移方程请看下图

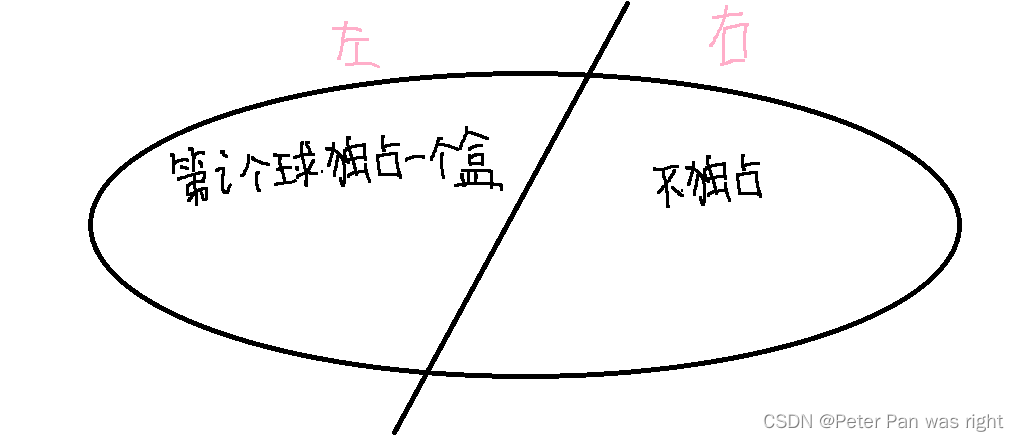
 第一种情况，左边：选完后变成m-1个装n-1个球，f[n-1][m-1]

第二种情况，右边：先让前n-1个球放m盒子，第n个球挑一盒

cin>>n>>m;
if(n<m){
	cout<<0<<endl;
	return 0;
}
for(ll i=1;i<=n;i++) S[i][1]=1;
for(ll j=2;j<=m;j++)
	for(ll i=j;i<=n;i++)
		S[i][j]=S[i-1][j-1]+j*S[i-1][j];
cout<S[n][m]<<endl;

不同的球放入不同的盒子

假设球相同，那么答案就是S[n][m]

然后再排列球，m!

因此，答案就是S[n][m]*m!

希望这些对大家有用，谢谢😀