目录

1、2、有序三元组的最大值 - 预处理前后最大值 + 遍历

（1）预处理前后值+遍历（枚举j） 

（2）枚举k

2、无限数组的最短子数组 - 前缀和 + 滑动窗口

---

1、2、有序三元组的最大值 - 预处理前后最大值 + 遍历

2874. 有序三元组中的最大值 II

（1）预处理前后值+遍历（枚举j） 

思路：

这题思路跟第368场的100114. 元素和最小的山形三元组 II很像

我自己写的！

我们可以预处理nums[j]的前后最大值pre[j]和beh[j]（在【1，n-2】范围内）

然后枚举【1，n-2】区间的（pre[i] - nums[i]）* beh[i]，更新最大值即可

这样可以保证ijk的下标顺序，也能顺利找到最大值

class Solution {
    public long maximumTripletValue(int[] nums) {
        long maxx=0;
        int n=nums.length;
        int[] pre=new int[n],beh=new int[n];
        pre[0]=nums[0];
        beh[n-1]=nums[n-1];
        
        for(int j=1;j<n-1;j++)
            if(nums[j-1]>pre[j-1]) pre[j]=nums[j-1];
            else pre[j]=pre[j-1];
        
        for(int j=n-2;j>0;j--)
            if(nums[j+1]>beh[j+1]) beh[j]=nums[j+1];
            else beh[j]=beh[j+1];
        
        for(int j=1;j<n-1;j++)
            maxx=Math.max(maxx,(long)(pre[j]-nums[j])*beh[j]);
        
        return maxx==0? 0:maxx;
    }
}

（2）枚举k

思路：

我们枚举k，然后维护k左边（nums[i]-nums[j]）的最大值

我们可以在遍历的过程中，维护 nums[i]的最大值 preMax，同时维护preMax 减当前元素的最大值 maxDiff，这就是 k 左边 nums[i]−nums[j] 的最大值。

class Solution {
    public long maximumTripletValue(int[] nums) {
        long maxx=0;
        int premaxdiff=0,premax=0;

        for(int x:nums)
        {
            maxx=Math.max(maxx,(long)premaxdiff*x);
            premaxdiff=Math.max(premaxdiff,premax-x);
            premax=Math.max(premax,x);
        }
        
        return maxx==0? 0:maxx;
    }
}

 

2、无限数组的最短子数组 - 前缀和 + 滑动窗口

2875. 无限数组的最短子数组

思路：

第一次思路跟灵神一样！激动！

设sum为数组值之和

因为求的是子数组的和，因此可以用前缀和优化

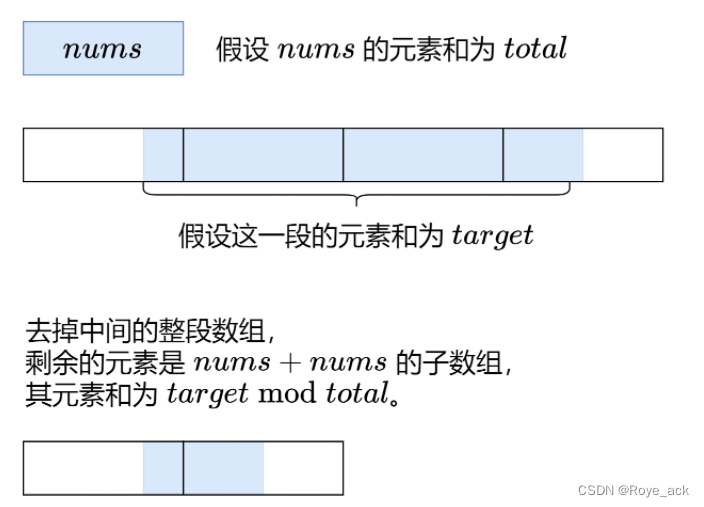
无穷个拼接数组，实际上就是【某后段+中间完整段+某前段】，中间完整段之和是固定的

因此我们可以只考虑两端拼接后的数组newnums，找newnums中子数组之和 = target%sum 的最短元素个数minx，最后答案返回minx+中间段数*数组元素个数即可

当我们去掉中间完整段后，找满足条件的最小子数组长度可以用滑动窗口

class Solution {
    public int minSizeSubarray(int[] nums, int target) {
        int n=nums.length,res=Integer.MAX_VALUE;
        long tol=0;
        
        int[] s=new int[2*n+1];

        for(int i=1;i<=2*n;i++) s[i]=s[i-1]+nums[(i-1)%n]; //求两段连起来的数组的前缀和
        
        int st=0;
        for(int ed=0;ed<2*n;ed++) //滑动窗口求最短元素个数
        {
            tol=s[ed+1]-s[st];
            while(tol>target%s[n])
            {
                tol-=nums[st++%n];
            }
            if(tol==target%s[n]) res=Math.min(res,ed-st+1);
        }

        return res==Integer.MAX_VALUE? -1:res+(int)(target/s[n])*n; //最后再加上中间省略的完整段
    }
}