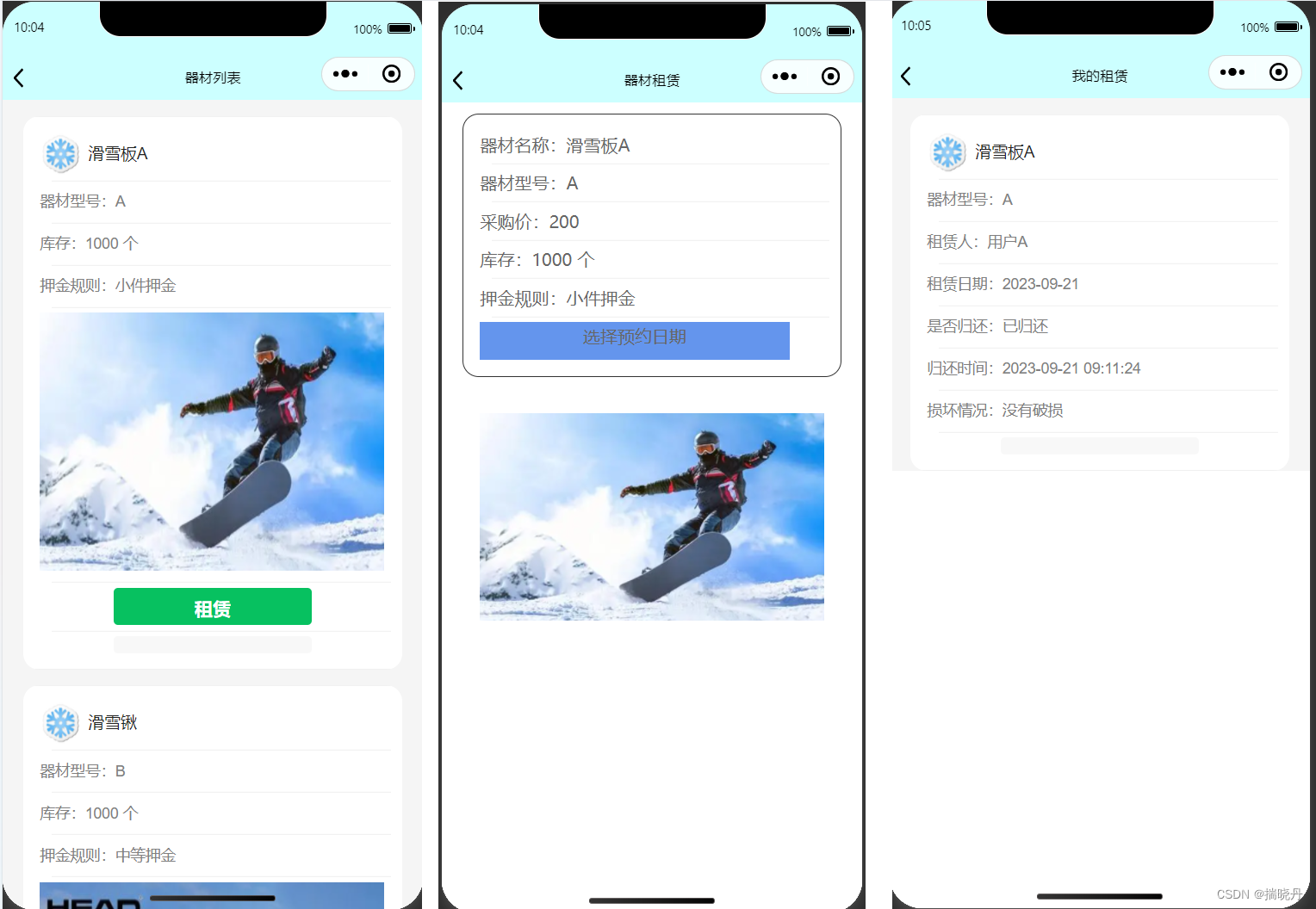
1、题目

问题描述

游戏“蓝桥争霸”由很多关卡和副本组成，每一关可以抽象为一个节点，整个游戏的关卡可以抽象为一棵树形图，每一关会有一道算法题，只有当经验值不低于第 $i$ 关的要求 $k_i$ 时，小蓝才能挑战成功通过此关，并且获得 $s_i$ 的经验值，每关的经验值只能获得一次。每个关卡（除了 1 号点）都会有一个前置关卡，只有通过了前置关卡，才能挑战后续关卡。

小蓝初始在 1 号点，也就是游戏开局初始点，同时具有一个初始经验值 $P$，它可以任何规划挑战顺序，想问你最多能够挑战成功多少道题。

小蓝会告诉你关卡的所有信息，以及他的初始经验值，你需要回答他组多能够挑战成功多少关卡。

输入格式

第一行输出两个整数 $n,P$，表示关卡的数量以及小蓝的初始经验值。

接下来 $n$ 行，每行输入三个整数 $f_i,s_i,k_i$，$f_i$ 表示每一关的前置关卡（$f_1$ 一定为0），$s_i$ 表示经验值，$k_i$ 表示挑战成功最少需要的经验值。

输出格式

一个整数，表示在最优的规划下，最多能挑战成功的关卡数量。

样例输入

4 5
0 3 5
1 2 8
1 3 9
3 1 15

样例输出

3

说明

游戏地图如下：

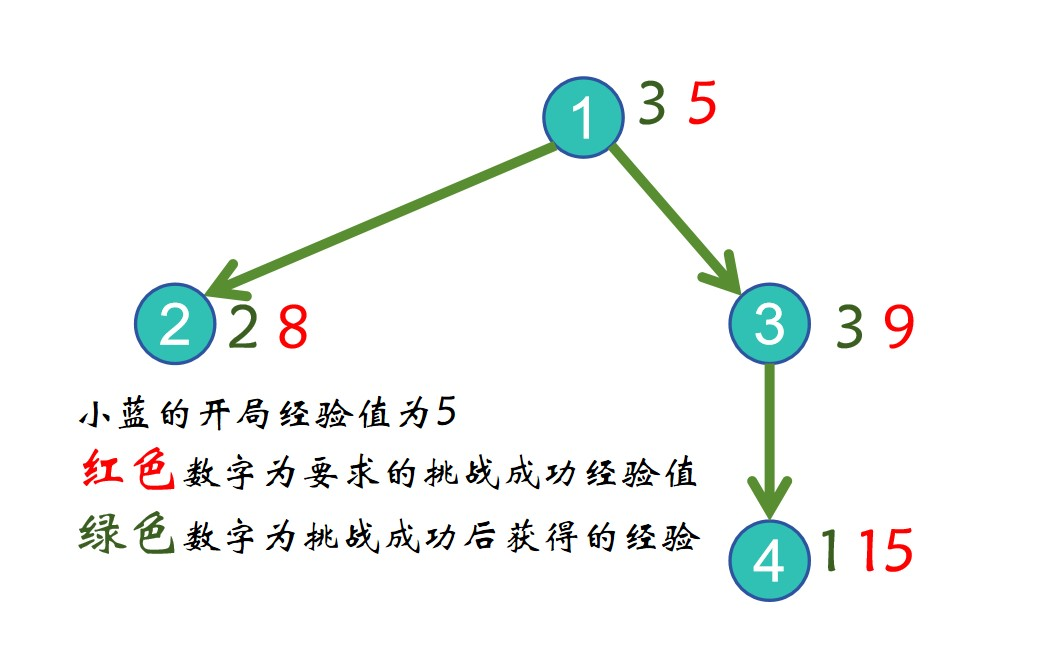
小蓝初始在 1 号关卡，初始经验为 5。每个关卡具有挑战前提：1 号关卡可以直接挑战，如果要挑战 2 号关卡，必须通过 1 号关卡，3,4 号关卡类似。

小蓝的一种挑战顺序如下：

1. 由于初始经验为 5，满足 1 号关卡要求，所以可以直接挑战成功 1 号关卡，获得 3 经验值，此时经验值为 8，并且获得挑战 2，3号关卡的机会。
2. 此时经验为 8，满足 2 号关卡要求，但是不满足 3 号要求，所以可以直接挑战成功 2 号关卡，获得 2 经验值，此时经验值为 10。
3. 此时经验为 10，满足 3 号关卡要求，所以对 3 号关卡挑战成功，获得 3 经验值，此时经验值为 13，并且获得挑战 4 号关卡的机会。
4. 此时经验为 13，小于 4 号关卡要求，所以无法成功挑战 4 号关卡，游戏无法继续。

数据范围

$f_1=0<f_i\le n\le 10^5,0\le P,s_i,k_i\le 10^9$。

数据保证输入为一棵树，并且根节点为 1。

原题链接

通关

2、思路

考察堆的数据结构 (STL的优先队列）

维护一个小根堆，每个节点维护两个值：节点编号和节点需要的经验值（或者说是难度），以难度为关键字建立小根堆（或者使用优先队列），通过节点 $u$ 后，将 $u$ 的所有直系儿子放入小根堆，每次取出最小难度的题目进行尝试，成功完成后获得奖励经验，并且将该节点的后续节点加入小根堆中，如此反复即可。

时间复杂度：$O(nlogn)$

3、代码

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#include <assert.h>

using namespace std;

typedef long long ll;
const int N = 1e5+100;
const int MOD = 998244353;

typedef pair<int, int> Pair;

vector<int> G[N];
int S[N], K[N];
int n, P;
int cnt = 0, vis[N];

void sol() {
    int f;
    cin >> n >> P;
    for (int i = 1; i <= n; ++i) {
        cin >> f >> S[i] >> K[i];
         G[f].push_back(i);
    }

    priority_queue<Pair, vector<Pair>, greater<Pair> > q;
    q.push({0, 0});
    int ccnt = -1;
    while (!q.empty()) {
        if (P >= q.top().first) {
            ccnt ++;
            Pair tmp = q.top();
            q.pop();
            P += S[tmp.second];
            for (int v : G[tmp.second]) {
                q.push({K[v], v});
            }
        } else {
            break;
        }
    }
    cout << ccnt << '\n';
}

int main() {
    sol();
    exit(0);
}