一起学数据结构(12)——归并排序的实现

news2024/10/1 7:36:10

1. 归并排序原理：

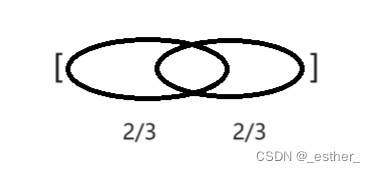
归并排序的大概原理如下图所示：

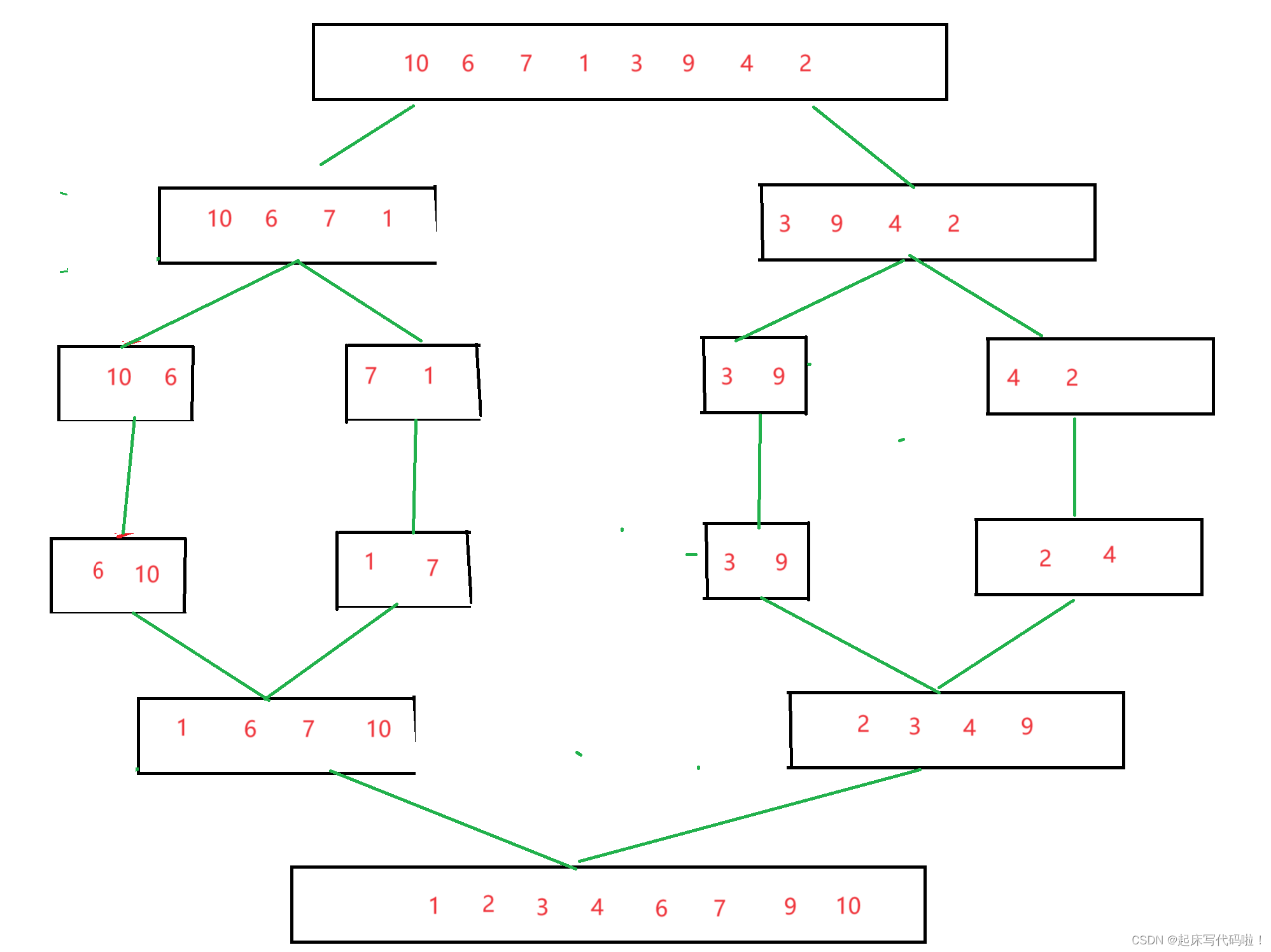
从图中可以看出，归并排序的整体思路就是把已给数组不断分成左右两个区间，当这个区间中的数据数量到达一定数值时，便返回去进行排序，整体的结构类似二叉树的结构，因此，对于归并排序同样可以利用递归进行实现。

对于递归实现归并排序，首先需要实现的第一步便是如何区分左右区间，在快速排序中，虽然在递归时依然同样需要根据一个值来区分左右区间，但是用于区分左右区间的值是在左右两边遍历数组时自动选出来的，对于归并排序，通过观察可以发现，归并排序的左右区间是通过数组下标的中间值进行区分的，为了方便表示，将这个中间值命名为 $mid$ ，例如，数组在进行第一次区分左右区间时，左区间的范围是 $[0,3]$ ,右区间的范围是 $[4,7]$ ，通过计算不难得到 $mid = 3$ ，所以，对于数组左右区间的划分，可以通过 $mid$ ， $begin$ (数组下标起始), $end$ (数组下标末位来划分）即

左区间范围： $[0,mid]$

右区间范围： $[mid+1,end]$

同时，在图中当区间中的数值数量为 $2$ 后，下一步直接进行排序，此处图中省略了区间分为两个区间数值数量为 $1$ 的两个区间的过程，这是因为，在区间中的数值数量 $< 2$ 时，便停止划分区间

所以，对于区间划分这部分的递归，可以用代码表示为：

 //归并排序
 void _MergeSort(int* a, int begin, int end)
 {
	 if (begin >= end)
	 {
		 return;
	 }

	 int mid = (begin + end) / 2;

	 MergeSort(a, begin, mid);
	 MergeSort(a,mid + 1, end);
 }

在区间划分结束后，就需要对数组进行排序。这里需要注意，在进行排序时，不能直接在原本已有的数组进行排序，为了解决这个问题，本文选择独立开辟一块空间用于排序，当一部分区间在这部分空间排序完成后，便将这部分内容返回到原数组，开辟空间的过程如下：

 void MergeSort(int* a, int begin, int end)
 {
	 int* tmp = (int*)malloc(sizeof(int) * (end - begin + 1));
	 if (tmp == NULL)
	 {
		 perror("malloc fail");

	 }
	 _MergeSort(a, tmp, begin, end);
 }

因为开辟的空间需要在上面的函数中使用，所以对于函数的定义需要更改为上图中的格式。

对于如何排序，文章给出下面的方法：

对于一个区间，定义四个变量，分别为： $begin1,$ $end1$ , $begin2$ , $end2$ ，具体使用方法如下：

令 $begin1 = begin$ , $end1 = mid$ , $begin2 = mid+1$ , $end2 = end$ ,具体使用方法如下方的代码所示：

 //归并排序
 void _MergeSort(int* a,int* tmp, int begin, int end)
 {
	 if (begin >= end)
	 {
		 return;
	 }

	 int mid = (begin + end) / 2;

	 _MergeSort(a,tmp, begin, mid);
	 _MergeSort(a,tmp,mid + 1, end);

	 int begin1 = begin, end1 = mid;
	 int begin2 = mid + 1, end2 = end;
	 int index = begin;
	 while (begin1 <= end1 && begin2 <= end2)
	 {
		 if (a[begin1] < a[begin2])
		 {
			 tmp[index++] = a[begin1++];
		 }
		 else
		 {
			 tmp[index++] = a[begin2++];
		 }
	 }
	 while (begin1 <= end1)
	 {
		 tmp[index++] = a[begin1++];
	 }
	 while (begin2 <= end2)
	 {
		 tmp[index++] = a[begin2++];
	 }
	 memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
 }

为了方便解释代码内容，给出下面的图像：

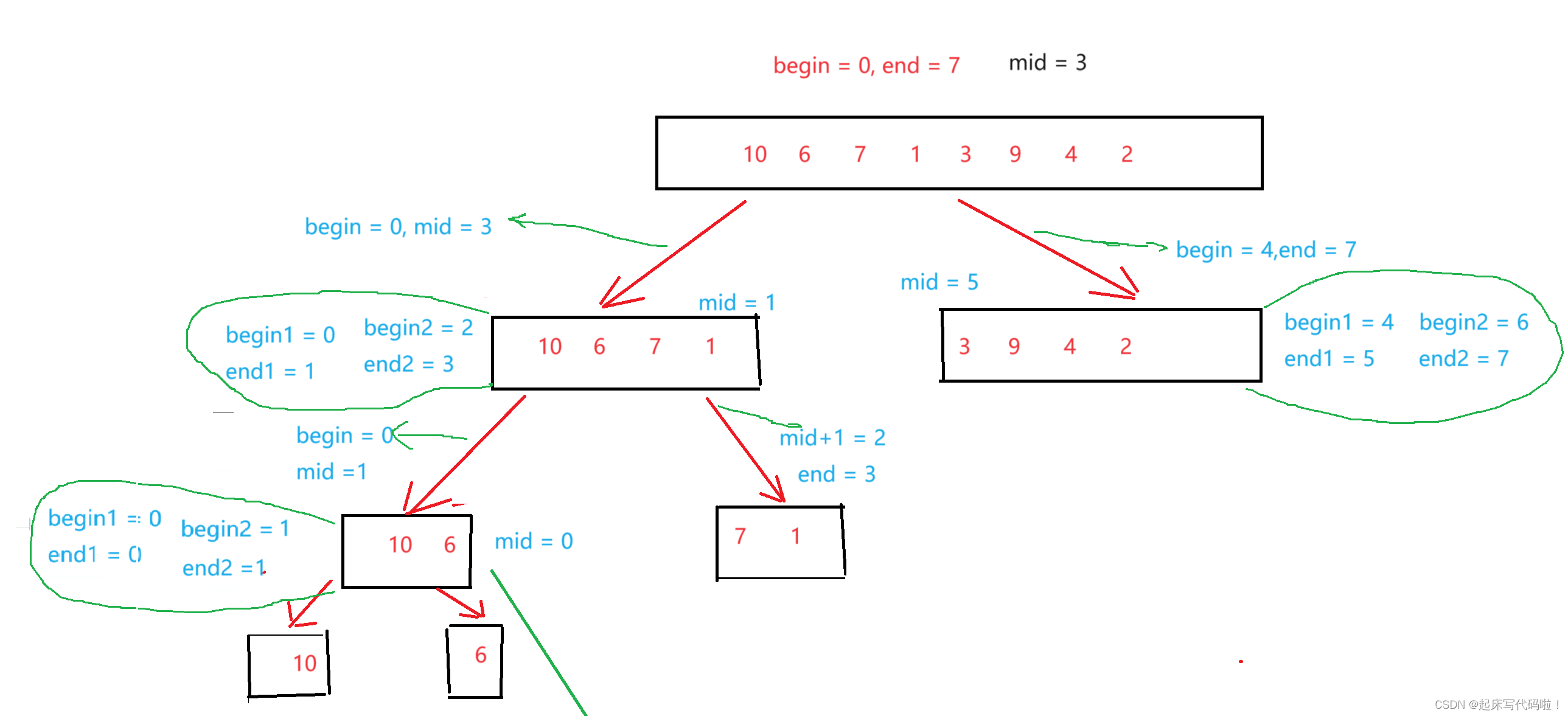
首先对左右区间进行区分，期间各个区间的 $begin1,$ $end1$ , $begin2$ , $end2$ ，如图所示，当区间数据数量 $< 2$ 时，停止区分区间进行排序，例如对 $[10,6]$ 这个区间，如果 $a[begin1] < a[begin2]$ ，则让小的哪个值插入到 $tmp$ ，此时 $tmp$ 中的内容如下图所示：

向原数组拷贝数值后，原数组左区间数值如下：

在 $[10,6]$ 区间遍历完成后，再遍历 $[7,1]$ 区间，由于 $begin$ 的不同，再数据调整完拷贝到 $tmp$ 后， $tmp$ 数组内容为：

随后再向原数组中拷贝，原数组内容为

对于其他的序列，依旧按照此规律，此部分不再叙述。

测试函数如下：

void TestMergeSort()
{
	int i[] = { 10,6,7,1,3,9,4,2 };
	int size = sizeof(i) / sizeof(int);
	MergeSort(i, 0, size - 1);
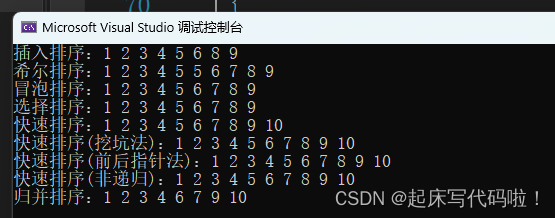
	printf("归并排序：");
	ArrayPrint(i, size);
}

运行结果如下：