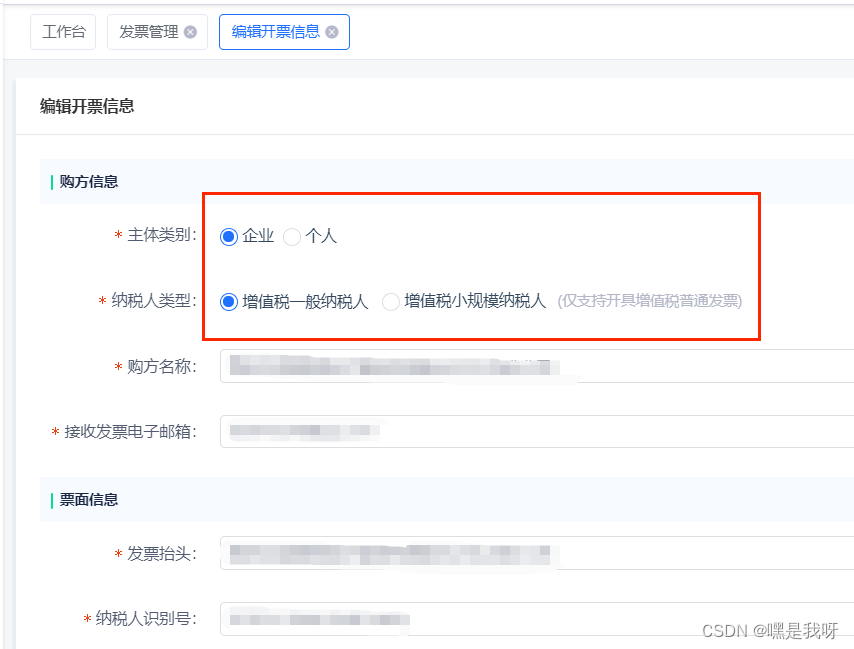
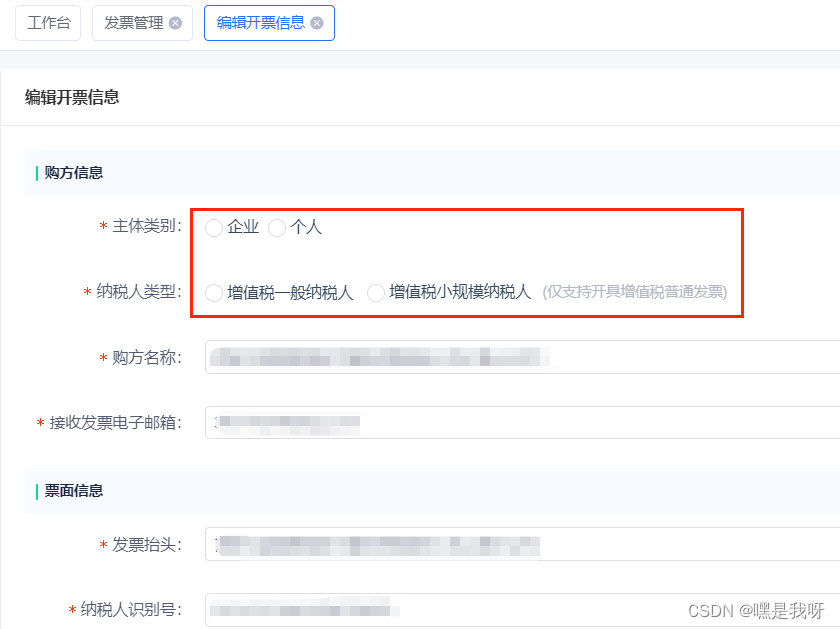
iview项目中,radio选中值回显问题
news2026/2/17 22:17:52
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1129039.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【ARM AMBA Q_Channel 详细介绍】
文章目录 1.1 Q_Channel 概述1.2 Q-Channel1.2.1 Q-Channel 接口1.2.2 Q-Channel 接口的握手状态1.2.3 握手信号规则 1.3 P_Channel的握手协议1.3.1 device 接受 PMU 的 power 请求1.3.2 device 拒绝 PMU 的 power 请求 1.4 device 复位信号与 Q _Channel 的结合1.4.1 RESETn 复…
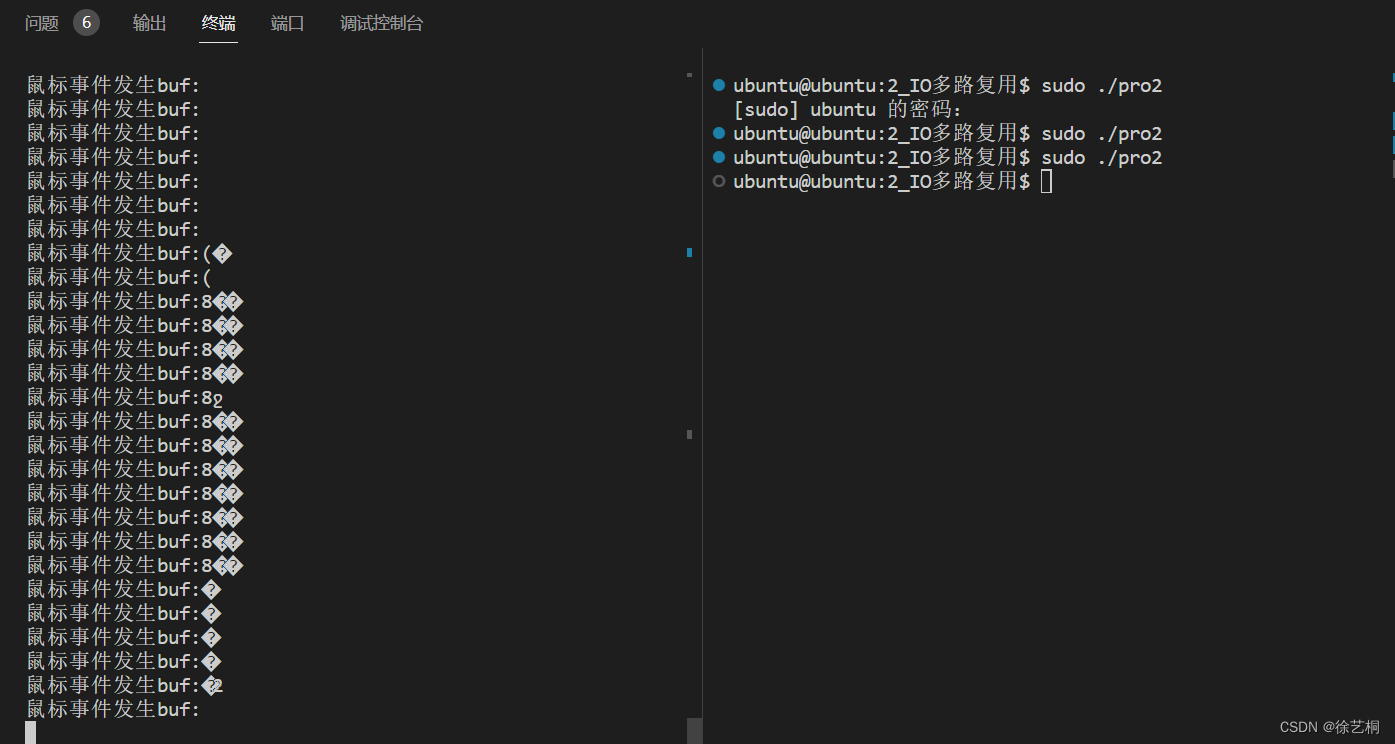
驱动开发5 阻塞IO实例、IO多路复用
1 阻塞IO
进程1
#include <stdlib.h>
#include <stdio.h>
#include <sys/types.h>
#include <sys/stat.h>
#include <sys/ioctl.h>
#include <fcntl.h>
#include <unistd.h>
#include <string.h>int main(int argc, char co…
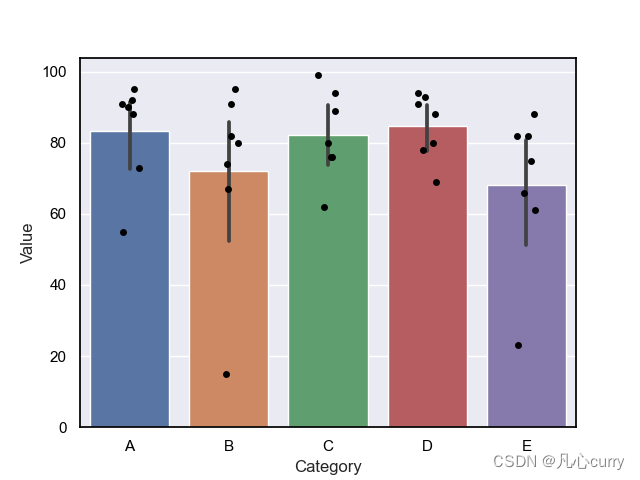
Python创建条形图加点重叠
目录 代码效果图 要使用Python的Seaborn库创建一个条形图加点重叠的统计图,可以使用
seaborn.barplot和
seaborn.stripplot函数。以下是一个论文级别的简单示例代码,演示如何创建这种效果的图 代码
import seaborn as sns
import matplotlib.pyplot a…
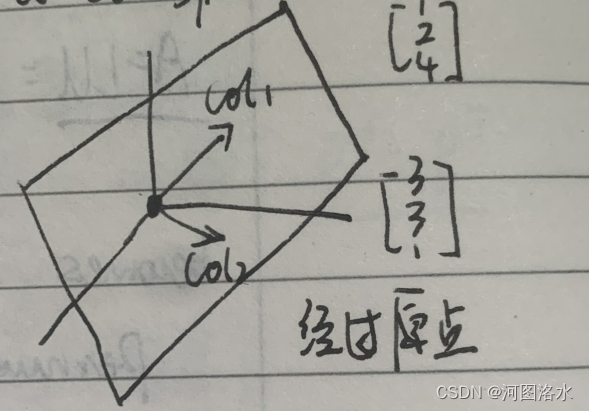
05 MIT线性代数-转置,置换,向量空间Transposes, permutations, spaces
1. Permutations P:
execute row exchanges
becomes PA LU for any invertible A
Permutations P identity matrix with reordered rows
mn (n-1) ... (3) (2) (1) counts recordings, counts all nxn permuations
对于nxn矩阵存在着n!个置换矩阵
,
2. Transpose: 2.…
如何将 huggingface上的模型文件下载到本地
写在前面
缘由:国内的GPU服务器直接调取 huggingface 上模型经常会失败,因此下载到本地就能免去许多麻烦。
方法三基于知乎上一位博主所提出方法的基础上进行改进,可以将huggingface上模型由 Colab 存进 谷歌云盘 或者 百度云盘。特别是有些…
Appium+Python+pytest自动化测试框架的实战
本文主要介绍了AppiumPythonpytest自动化测试框架的实战,文中通过示例代码介绍的非常详细,具有一定的参考价值,感兴趣的小伙伴们可以参考一下
先简单介绍一下目录,再贴一些代码,代码里有注释
Basic目录下写的是一些公…
【文章学习系列之模型】Koopa
本章内容 文章概况模型结构主要结构实验结果消融实验模型效率分解效果定性分解效果定量算子稳定性 总结 文章概况
《Koopa: Learning Non-stationary Time Series Dynamics with Koopman Predictors》是2023年发表于NeurIPS的一篇论文。考虑到时序预测中训练和推理数据之间甚至…
网工内推 | 网络工程师,大专以上、HCIA认证即可,最高14薪
01 湖南口味王集团 招聘岗位:网络工程师 职责描述:
1、负责园区内电脑日常维护; 2、负责园区内办公周边设备的日常维护,如打印机、投影仪等; 3、负责园区内电话日常维护; 4、负责园区内信息资产管理&#…
vcomp100.dll丢失的解决方法,一键修复vcomp100.dll丢失问题
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“vcomp100.dll丢失”。这个错误通常会导致某些程序无法正常运行,给用户带来困扰。为了解决这个问题,我整理了以下五个解决方法,希望能对大家有所帮助。 一…
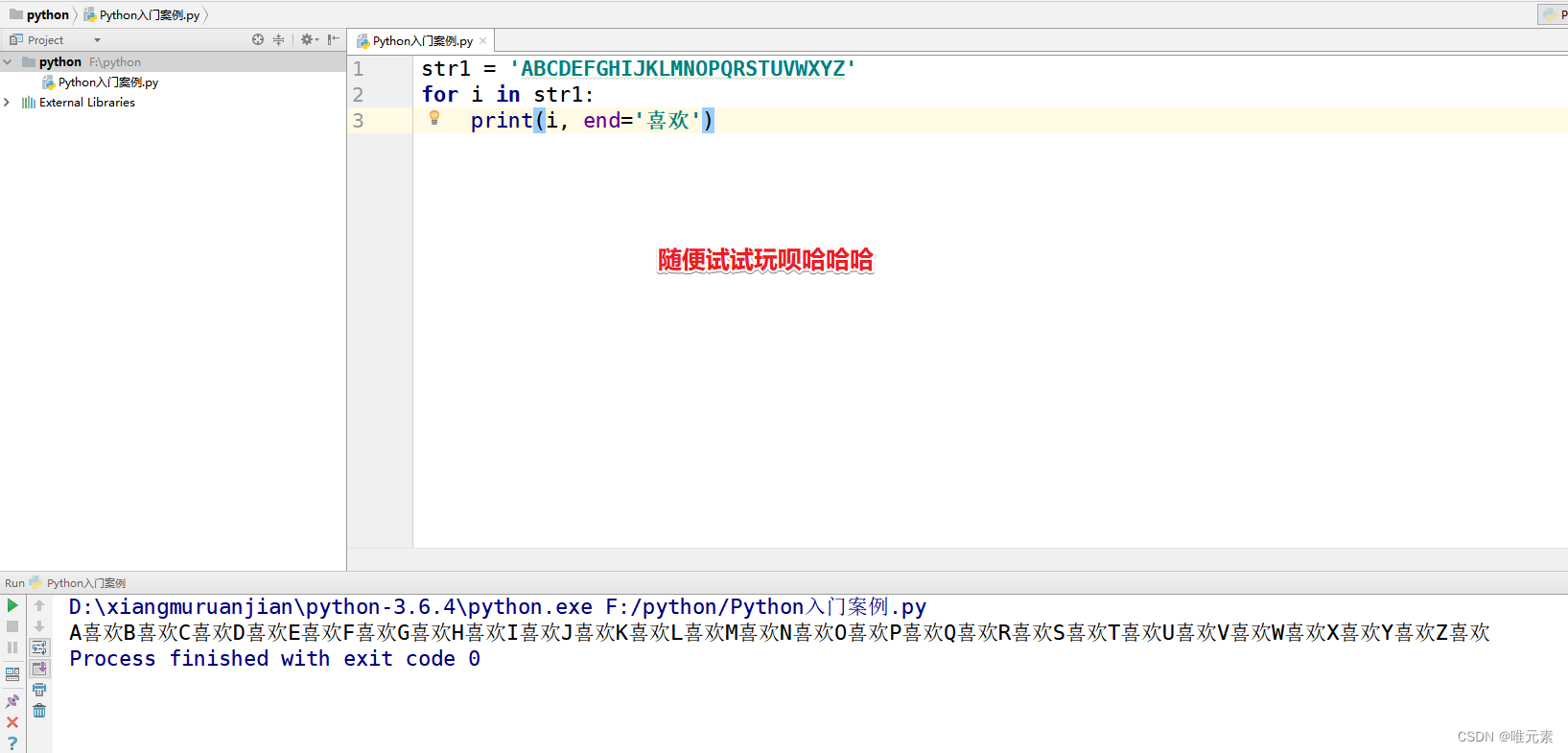
Python-----for循环基本语法及其应用---对序列进行遍历循环
for循环基本语法
for循环结构主要用于(序列 :包括 字符串、列表、元组、集合以及字典)类型数据的遍历(循环)操作。
遍历(Traversal),是指沿着某条搜索路线,依次对树(或图&#…
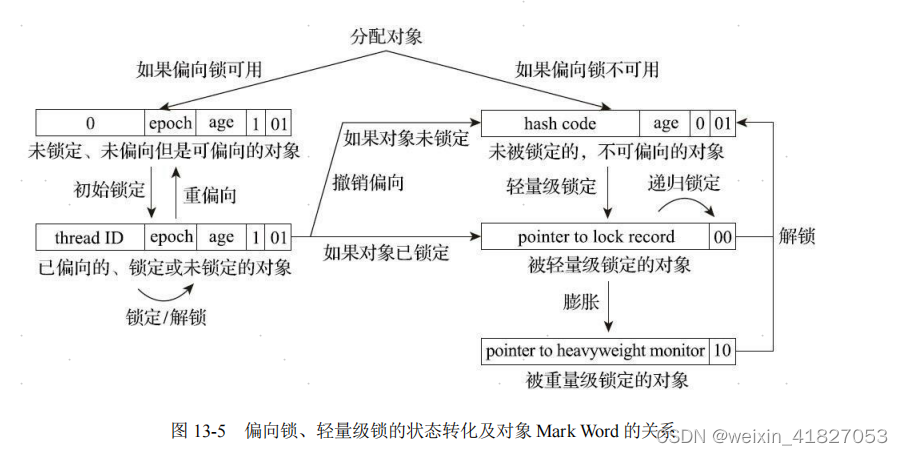
《深入理解java虚拟机 第三版》学习笔记三
第 8 章 虚拟机字节码执行引擎
代码编译的结果从本地机器码转变为字节码,是存储格式发展的一小步,却是编程语言发展的一大步。
8.1 概述
执行引擎是 Java 虚拟机核心的组成部分之一。“虚拟机”是一个相对于“物理机”的概念,这两种机器都…
Python3 + Appium + 安卓模拟器实现APP自动化测试并生成测试报告
这篇文章主要介绍了Python3 Appium 安卓模拟器实现APP自动化测试并生成测试报告,本文给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友可以参考下
正文
一、安装Python3
直接登录Python官网https://www.python.org/&…
C++数据结构X篇_21_插入排序(稳定的排序)
文章目录 1. 插入排序原理2. 算法图解3. 核心代码:4. 插入排序整体代码实现 1. 插入排序原理
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相…
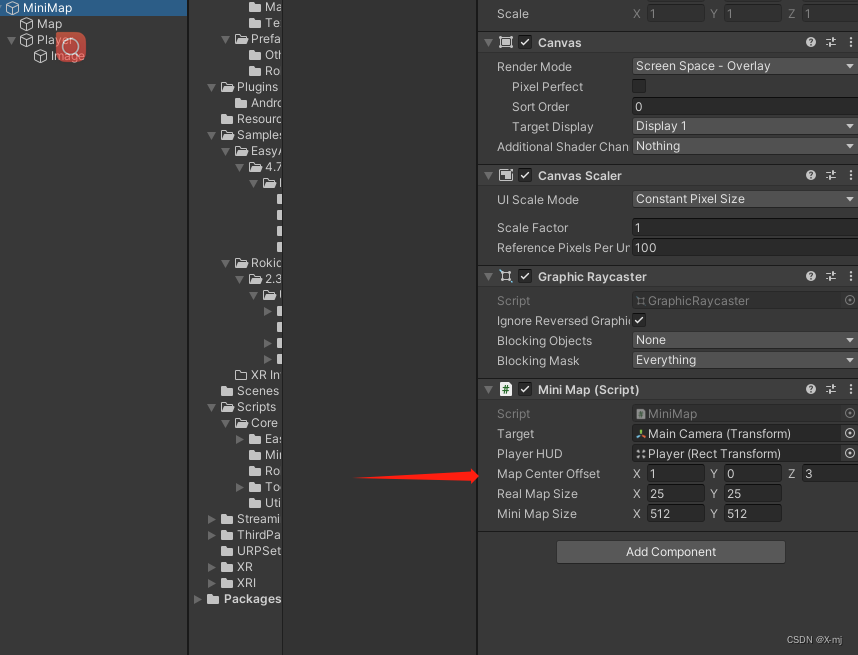
Unity 自定义小地图
最近工作做了个小地图,再此记录下思路。
1、准备所需素材 显示为地图(我们取顶视图)。创建一个Cube,缩放到可以把实际地图包住。实际地图的尺寸和偏移量 。我这里长宽都是25,偏移量(1,0&…
MySQL进阶(数据库引擎)——MyISAM和InnoDB引擎的区别
1.是否支持行级锁
MyISAM 只有表级锁,而InnoDB 支持行级锁和表级锁,默认为行级锁。
(1)MySQL大致可以归纳为以下3种锁:
表级锁:开销小,加锁快;不会出现死锁;锁的粒度大…
C# FileInfo类的使用方法及常用操作(附代码示例)
在C#编程中,处理文件操作是一项常见而重要的任务。为了更好地管理和操作文件,C#提供了一个强大且灵活的FileInfo类。本文将深入探讨C# FileInfo类的使用方法,并为您提供一些实用的代码示例。 目录 一、什么是FileInfo类?二、使用F…
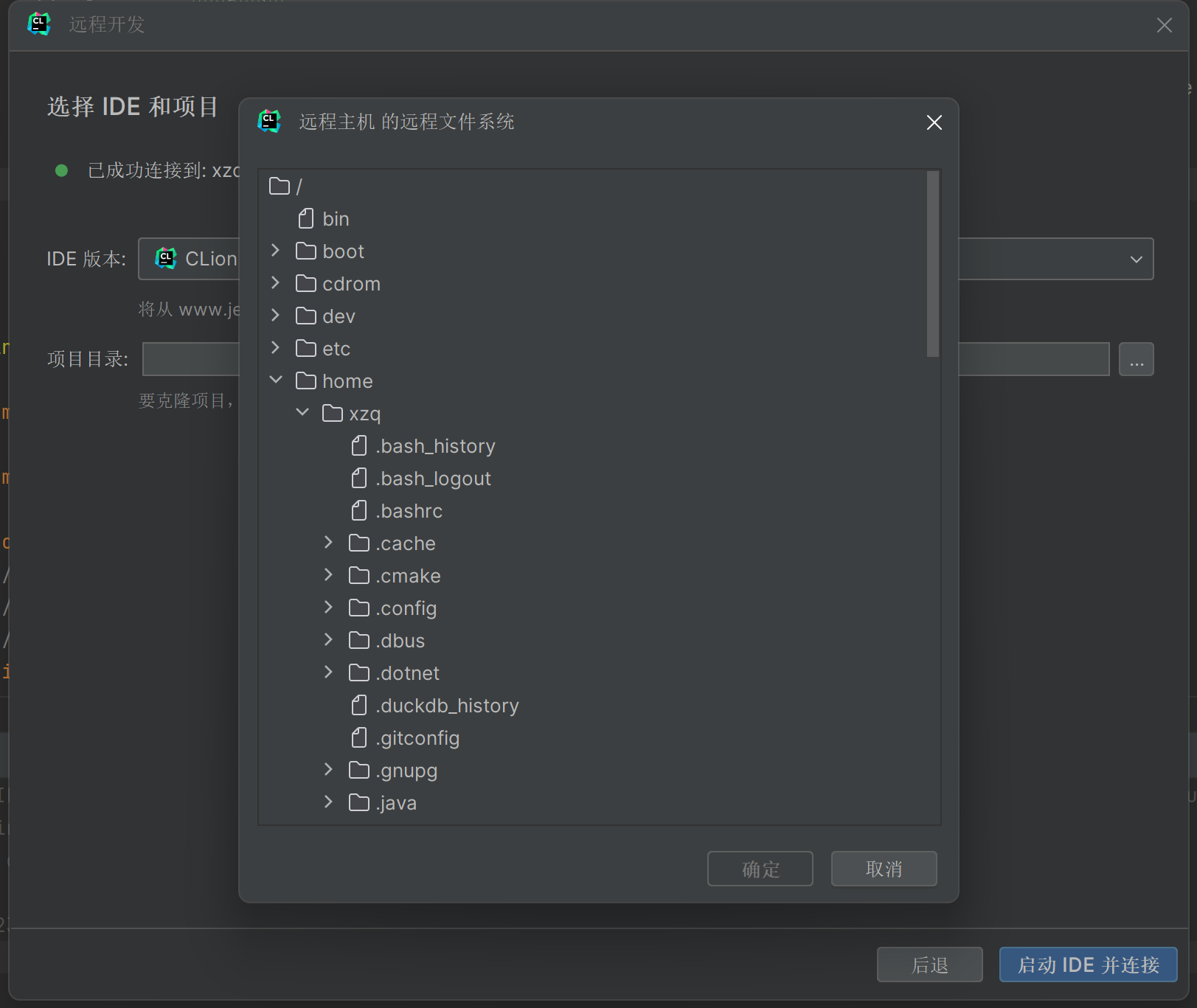
CLion使用SSH远程连接Linux服务器
最近要一直用实验室的服务器写Linux下的C代码, 本来一直用VScode(SSH)连接服务器, 但是我以前还是用JetBrains的IDE用的多, 毕竟他家的IDE代码提示和功能在某些细节上更加丰富。所以这次我使用了Clion里的远程连接(同样也是SSH工具)连接上了我的服务器, 实现了和VScode上同样的…
NOIP2023模拟1联测22 黑暗料理
NOIP2023模拟1联测22 黑暗料理 题目大意
自己看
思路 两个数相加能够产生质数的情况就是:11 或者 偶数质数 那么 1 1 1 不能保留超过一个 建一个图,原点连向所有奇数点,所有偶数点连向汇点,奇数点和偶数点的和为奇数的就相连 …