文章概况

《Koopa: Learning Non-stationary Time Series Dynamics with Koopman Predictors》是2023年发表于NeurIPS的一篇论文。考虑到时序预测中训练和推理数据之间甚至每个回溯窗口之间存在巨大的分布差距，作者结合动态模式分解(DMD)[近似库普曼算子的领先数值方法]，提出一种新的非平稳时序预测模型，实验表明模型轻量高效且具备分布变化的自适应能力。

文章代码链接：
文章链接
代码链接

模型结构

模型见上图橙框内容。模型由若干个Koopa Block组成，每一层Block输出两组数据，分别为残差项和预测项。其中下一个Block的输入由上一个Block的残差项提供，每个Block的预测项求和得到最终的模型预测值。

主要结构

Koopa Block见上图绿框内容。时间序列问题的分解方法一直广受欢迎，例如ARIMA，将时序数据分解为趋势项、季节项、周期项和残差项，尝试将非平稳数据预测问题分解为多个具有一定规律的数据外加残差数据进行预测。

本文作者同样进行分解操作，将原始数据分解为时变项和时常项。时常项是指在原始数据中包含的基本稳定不变的数值，如周期、幅值等。时变项是指除了时常项以外的其他内容。

为了达到分离时常项和时变项的目标，作者使用傅里叶滤波器对数据进行时频转化，选取前α比例的高频分量所在的时域数据作为时常项Xinv，相减后的其他项则作为时变项Xvar。随后再将两者分别输入到时常库普曼预测器(Time-invariant Koopman Predictor)和时变库普曼预测器(Time-variant Koopman Predictor)中。

时常库普曼预测器	时变库普曼预测器
Time-invariant Koopman Predictor	Time-variant Koopman Predictor
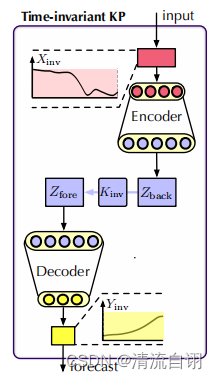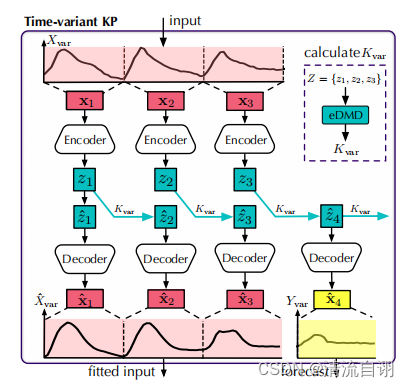在时常库普曼预测器中，时常项$X_{inv}$经由编码器得到$Z_{back}$，再在可学习矩阵$K_{inv}$的转换下得到$Z_{fore}$，最后通过解码器获得$Y_{inv}$。	在时变库普曼预测器中，时变项$X_{var}$被划分为$n$份，分别经由编码器获得$Z$，并与$K_{var}$相乘获得$\hat{Z}$，其中$K_{var}$是利用DMD方法对$Z$计算求得。需要注意的是，该部分作者利用Koopma算子$K_{var}$来模拟相邻时间片段之间的变化，如$Z_1$到${\hat{Z}}_2$，而${\hat{Z}}_1$因其无前置片段而直接继承$Z_1$的值。$\hat{Z}$在解码器的作用下获得$\hat{X}$。$\hat{X}$中前$n$项与$X_{var}$做差后输出，成为下一个Koopa Block的输入，即为残差项；$\hat{X}$中的最后一项与时常库普曼预测器的输出$Y_{inv}$求和作为最终预测结果的一部分，即为预测项。

实验结果

得益于作者所提的层次动态学习和时常变分离机制，以MLP为重要结构的Koopa占据了绝大多数的最佳项，具有优异的预测效果。相比之下，作为MLP模型的代表DLinear，其预报效果依旧不佳，再一次对比出作者所提结构的有效性。

消融实验

模型效率

作者从预测性能、训练速度和内存三个方面对模型效率进行对比，可以发现左下角红色标记在这三个方面中均遥遥领先。

分解效果定性

作者比较了分解效果。上图（左）通过对比时变项和时常项的标准差对比两者在不同任务中的差距，可以观察到时变和时常之间以及时变项存在显著的偏差，说明傅里叶成功地从频域中将两者进行分解。上图（右）则反映了局部算子可以在不同的时期表现出不同的变化，可解释为大值热力图对应上升趋势，小值则为下降。

分解效果定量

将只使用时常项、只使用时变项、替换为高低通滤波器、分支转换与本文方法对比，突出分解方法的有效性。

算子稳定性

作者对算子的稳定性进行分析。在上图中，左图是只有时常算子的单模块模型，中图是有着时常算子和时变算子的单模块模型，右图是有着时常算子和时变算子的双模块模型。可以看出红点分布逐渐接近圆弧且计算数值逐渐减小，这表明稳定性有所提高。

总结

这篇论文不同于先前的时序分解思路，而是从库普曼理论入手，将非平稳数据分解为时变和时常分量，并将MLP、残差穿差其中，其轻量高效与优秀的预测能力再一次告诉了我“穿丝佛门”确实未必。