🕺作者： 主页

我的专栏
C语言从0到1
探秘C++
数据结构从0到1
探秘Linux
菜鸟刷题集

😘欢迎关注：👍点赞🙌收藏✍️留言

🏇码字不易，你的👍点赞🙌收藏❤️关注对我真的很重要，有问题可在评论区提出，感谢阅读！！！

前言

本篇为回溯算法专题的刷题题单，总共5道题，每道题都有对应的链接。

边听歌边刷题吧~

Thank You

推荐刷题路线 → 《代码随想录》

77. 组合

链接：77. 组合

解题思路

一开始我想的就是最暴力的算法，直接枚举所有情况，使用for循环这样，但是不同的数量的选择使得这个办法用不起来

然后看了一眼代码随想录的思路，回溯算法，在二叉树专题的时候写过，但是没想到怎么应用到这道题

回溯算法，可以把它想象成一棵二叉树，然后碰到节点就处理，处理后再撤销

在这题就可以使用path数组来存贮“路径”，然后最后满足情况就取，不满足就舍去

解题步骤：

• 确定函数参数：n、k肯定是必要的，但是还需要一个参数来确定当前的递归遍历到哪个Index了

• 确定终止条件：k的含义是“要求k个数的组合”，可以看作树的深度，当path数组的长度等于k时就说明数量取够了

• 事件处理：从开始的index遍历，如果它小于n就可以将该数交给path，继续向下遍历，继续取数，函数的开始index需要往后挪一位，为了“尝试”其他的路径，在处理完后面的“事务”后就会把当前数字删掉去遍历其他的路径

AC代码

//未剪枝回溯算法
class Solution {
public:

    vector<vector<int>> res;
    vector<int> path;
    void backtraval(int n,int k,int startIndex){
        if(k==path.size()){
            res.push_back(path);
            return;
        }
        for(int i=startIndex;i<=n;++i){
            path.push_back(i);
            backtraval(n,k,i+1);
            path.pop_back();
        }
    }

    vector<vector<int>> combine(int n, int k) {
        res.clear();
        path.clear();
        backtraval(n,k,1);
        return res;
    }
};

//剪枝回溯算法
class Solution {
public:

    vector<vector<int>> res;
    vector<int> path;
    void backtraval(int n,int k,int startIndex){
        if(k==path.size()){
            res.push_back(path);
            return;
        }
        //path.size() : 现在path中的数量
        //k-path.size() : 还需要增加的数量
        //n - (k-path.size()) +1 : 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历
        for(int i=startIndex;i <= n - (k-path.size()) +1 ;++i){
            path.push_back(i);
            backtraval(n,k,i+1);
            path.pop_back();
        }
    }

    vector<vector<int>> combine(int n, int k) {
        res.clear();
        path.clear();
        backtraval(n,k,1);
        return res;
    }
};

216. 组合总和 III

链接：216. 组合总和 III

解题思路

• 和前面77题的思路类似，不过这个要求计算总和

• 所以我直接用总和来减

• 在终止条件中需要判断数的个数满足条件后，只要n==0就说明满足条件

AC代码

class Solution {
public:
    vector<vector<int>> com;
    vector<int> path;

    void travalback(int n,int k,int staticIndex){
        if(k==path.size()){
            if(n==0)com.push_back(path);
            return;
        }
        //当前剩余的数的和为n
        //如果开始的数大于剩下数的和，那么就没有意义了，所以for循环的条件就取min(9,n)
        //写成9也可以，但是一些本来就不满足条件的值就会重复进入循环
        for(int i=staticIndex;i<=min(9,n);++i){
            n-=i;
            path.push_back(i);
            travalback(n,k,i+1);
            path.pop_back();
            n+=i;
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        travalback(n,k,1);
        return com;
    }
};

39. 组合总和

链接：39. 组合总和

解题思路

• 更详细的@代码随想录

• 我的思路就是：它要组合就要遍历所有的选择，使用回溯算法加减数就可以了

• 参数：原来的canducates 、target，肯定是需要的，还需要一个参数sum来记录总数和，一个参数staicIndex记录从数组的哪个位置开始

• 终止条件：当总数=目标值时就可以停下来判断是否=目标值了

• for循环：初始值就是staicIndex，条件是candicates的数组长度并且可以同时加上一个条件，当前的值加上总数是否≤目标值，如果是的话就继续，这样就不用多一次调用函数了

• for循环内部：sum先加上candidates[i]，path先将candidates[i]加入数组，再调用函数后再撤销

• 注意candicates要先排序，这样就可以从最小的数开始

AC代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;

    void travalBack(vector<int>& candidates, int& target ,int sum,int staicIndex){
        if(sum == target){
            res.push_back(path);
            return;
        }

        for(int i=staicIndex;i<candidates.size()&&sum + candidates[i] <= target;++i){
            sum+=candidates[i];
            path.push_back(candidates[i]);
            travalBack(candidates,target,sum,i);
            path.pop_back();
            sum-=candidates[i];
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        travalBack(candidates,target,0,0);
        return res;
    }
};

40. 组合总和 II

链接：40. 组合总和 II

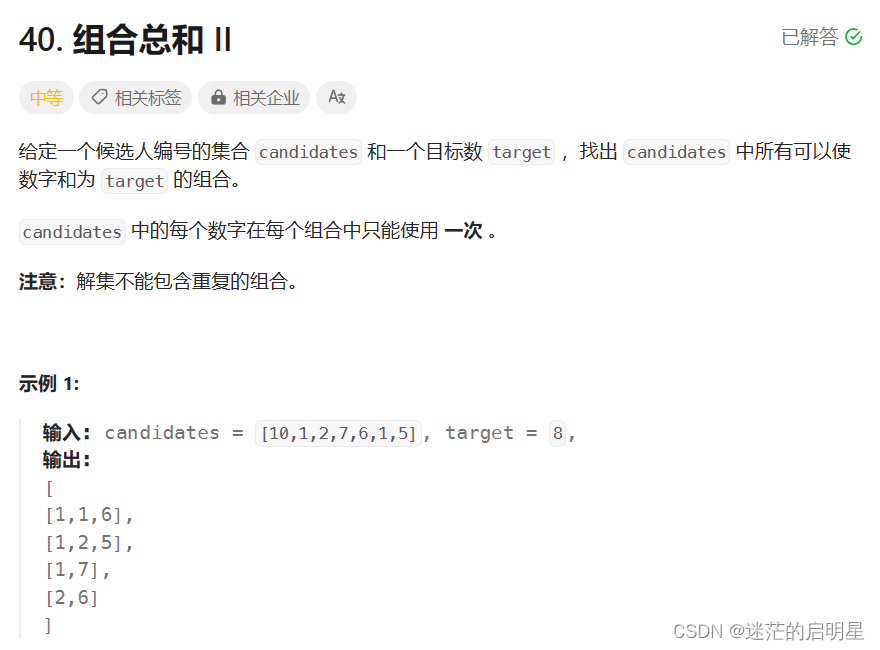
解题思路

• 依旧是推荐看@代码随想录

• 以下是个人的思路

• 首先可以知道的是最后的结果中不能含有重复的组合，如果要使用最后去重的方法的话很容易超时，所以只能在回溯算法中想办法

• 显然当前的值如果和前面的值相等就说明肯定会有重复的组合

• 怎么规避这样的情况呢？首先要说明的是我们应该是在for循环里处理这件事，因为我们是在for循环中选择当前的值的，其次还需要一个变量来记录前一个值是否被“取”过，我们用used[ ]来存储，如果是false，说明没有被“取”，此时就不能取当前的值，因为前一个值为当前节点的时候必然取过现在的当前节点，也就必然会重复。代码如下。

• 还有这一句 travalBack(candidates,target-candidates[i],i+1,used);当进入它时，参数target就减去了candidates[i]，但其实在现在函数的target并没有改变，也就实现了回溯的目的。

• 很多话用语言很难表达，建议看看代码随想录的视频方便理解。

• 剩下其他的其实没有说明好说的，和前面的回溯相关的题目一样

AC代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    void travalBack(vector<int>& candidates, int target, int staticIndex,vector<bool>&used)
    {
        if(target==0){
            res.push_back(path);
            return;
        }

        for(int i=staticIndex;i<candidates.size()&&target-candidates[i]>=0;++i)
        {
            if(i>0&&candidates[i]==candidates[i-1]&&used[i-1]==false)continue;
            path.push_back(candidates[i]);
            used[i]=true;
            travalBack(candidates,target-candidates[i],i+1,used);
            used[i]=false;
            path.pop_back();
        }
    }

    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        if(candidates.size()==0)return res;
        vector<bool> used(candidates.size(),false);
        sort(candidates.begin(),candidates.end());
        travalBack(candidates,target,0,used);
        return res;
    }
};

131. 分割回文串

链接：131. 分割回文串

解题思路

一开始我老是想把判断是否是回文数的条件放在终止条件里面，但是发现不对劲却又说不上来，看了一眼题解@代码随想录，是我想的分割字符串的方式不对，它是要把满足回文数的子串保留，我那样的话没有分割，只是遍历了一次，做不到让子串的长度变化，而且还不能看到每一种情况。

总结如下：

• 看到题目就要了解到可以使用回溯，但是难点在于如何分割子串

• 如何分割子串？我们之前写回溯相关的题目时总会用到一个变量staticIndex，这是当我们需要一个参照物的时候，就需要这个变量来记录，然后随着for循环中i的增长，我们可选择的子串的长度就会增长，我们只需要判断从参照物staticIndex到i这一段的字符串是否满足回文数，如果满足就可以继续下一步，将这个子串保留，否则还是继续增长子串，在从处理下一步的函数中出来的时候，我们需要将path的最后的子串去掉，恢复现场去查询其他的子串。

AC代码

class Solution {
public:
    vector<vector<string>> res;
    vector<string> path;
    void travalback(string& s,int staticIndex)
    {
        if(staticIndex>=s.size())
        {
            res.push_back(path);
            return;
        }

        for(int i=staticIndex;i<s.size();++i)
        {
          //判断是否为回文数
            string p=s.substr(staticIndex,i-staticIndex+1);
            string q=p;
            reverse(p.begin(),p.end());
            if(p==q){
                path.push_back(p);
                travalback(s,i+1);//注意是i+1，取过不能再取
                path.pop_back();
            }else{
                continue;
            }
        }
    }
    vector<vector<string>> partition(string s) {
        if(s.size()==0)return res;
        travalback(s,0);
        return res;
    }
};