这次是动态规划最后一期了，感谢大家一直以来的观看，以后就进入新的篇章了

  

目录

题目：照相排列

  思路：  

  

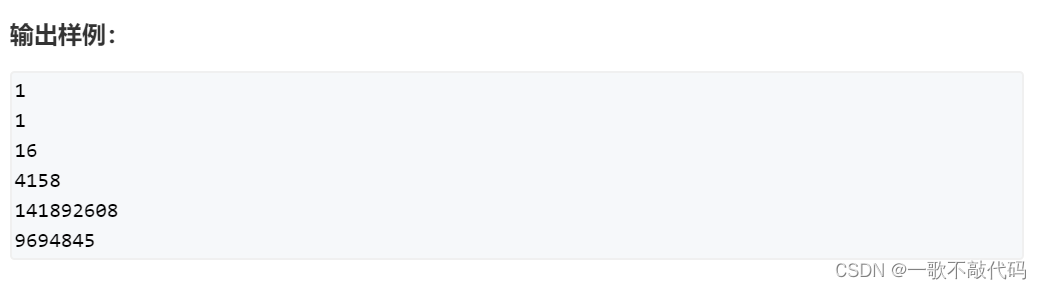
题目：照相排列

    

    

思路：  

首先记录状态f[a][b][c][d][e]表示每排如此人数下对应的方案数，然后发现第一排人数大于第二排时，第一排最后一个人可有可无，那就好做了。

   
故f[a,bcde]=f[a-1,bcde],同理其余排也如此转移，这样此状态的所有来源都知道了，即：f[abcde]=f[a-1]+f[b-1]+f[c-1]+f[d-1]+f[e-1]    
   

#include <bits/stdc++.h>  
using namespace std;
typedef long long LL;                                                                                          
const int N = 31;
int n;
LL f[N][N][N][N][N];
int main()
{
    while (cin>>n,n)
    {
        int s[5] = {0};
        for (int i=0; i<n; i++) cin>>s[i];
        f[0][0][0][0][0]=1;
        for (int a=0; a<=s[0]; a++)
            for (int b=0; b<=min(a,s[1]); b++)
                for (int c=0; c<=min(b,s[2]); c++)
                    for (int d=0; d<=min(c,s[3]); d++)
                        for (int e=0; e<=min(d,s[4]); e++)
                        {
                            LL &x = f[a][b][c][d][e];
                            if (a&&a-1>=b) x+=f[a-1][b][c][d][e];
                            if (b&&b-1>=c) x+=f[a][b-1][c][d][e];
                            if (c&&c-1>=d) x+=f[a][b][c-1][d][e];
                            if (d&&d-1>=e) x+=f[a][b][c][d-1][e];
                            if (e) x += f[a][b][c][d][e-1];
                        }
        cout <<f[s[0]][s[1]][s[2]][s[3]][s[4]]<< endl;
    }
    return 0;
}

各位宝程序员节快乐！