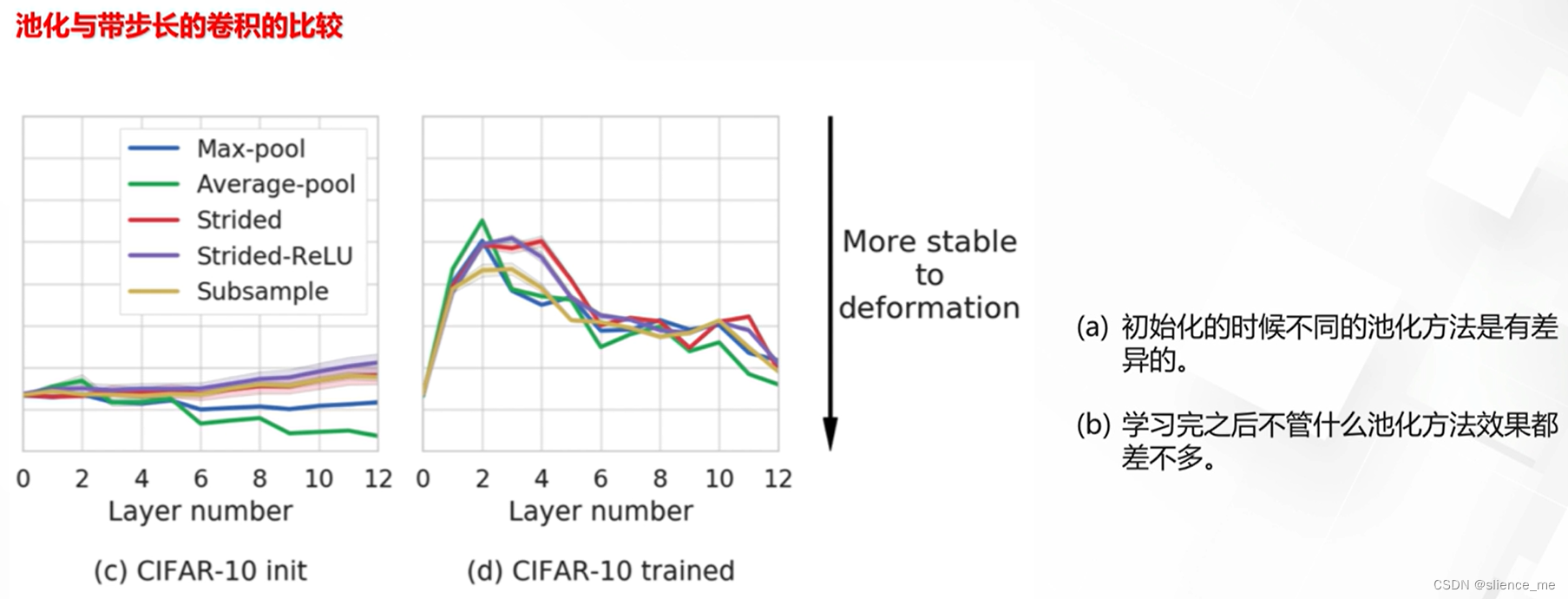
点集合的三角剖分是指如何将一些离散的点集合组合成不均匀的三角形网格,使得每个点成为三角网中三角面的顶点。这个算法的用处很多,一个典型的意义在于可以通过一堆离散点构建的TIN实现对整个构网区域的线性控制,比如用带高程的离散点构建的TIN来表达地形。
在实际工作中,使用最多的三角剖分是Delaunay三角剖分。通过Delaunay三角剖分算法能够构建一个具有空圆特性和最大化最小角特性的三角网。空圆特性其实就是对于两个共边的三角形,任意一个三角形的外接圆中都不能包含有另一个三角形的顶点,这种形式的剖分产生的最小角最大。这些特性可能有些难以理解,但是我们可以先谨记一点:Delaunay三角网是一种特性最优的三角剖分。
通过CGAL,我们可以直接通过离散点集生成Delaunay三角网,实现代码如下:
#include <CGAL/Delaunay_triangulation_2.h>
#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Projection_traits_xy_3.h>
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Projection_traits_xy_3<K> Gt;
typedef CGAL::Delaunay_triangulation_2<Gt> Delaunay;
typedef K::Point_3 Point;
#include <ogrsf_frmts.h>
#include <iostream>
#include <string>
using namespace std;
bool ReadVector(vector<Point> &vertexList) {
string srcFile = "Data/Vector/points.shp";
GDALDataset *poDS = (GDALDataset *)GDALOpenEx(srcFile.c_str(), GDAL_OF_VECTOR,
NULL, NULL, NULL);
if (!poDS) {
printf("无法读取该文件,请检查数据是否存在问题!");
return false;
}
if (poDS->GetLayerCount() < 1) {
printf("该文件的层数小于1,请检查数据是否存在问题!");
return false;
}
for (int li = 0; li < poDS->GetLayerCount(); li++) {
OGRLayer *poLayer = poDS->GetLayer(li); //读取层
poLayer->ResetReading();
//遍历特征
OGRFeature *poFeature = nullptr;
while ((poFeature = poLayer->GetNextFeature()) != nullptr) {
OGRGeometry *geometry = poFeature->GetGeometryRef();
OGRwkbGeometryType geometryType = geometry->getGeometryType();
switch (geometryType) {
case wkbPoint:
case wkbPointM:
case wkbPointZM: {
OGRPoint *ogrPoint = dynamic_cast<OGRPoint *>(geometry);
if (ogrPoint) {
vertexList.emplace_back(ogrPoint->getX(), ogrPoint->getY(), 0);
}
break;
}
case wkbMultiPoint:
case wkbMultiPointM:
case wkbMultiPointZM: {
OGRMultiPoint *ogrMultiPoint =
dynamic_cast<OGRMultiPoint *>(geometry);
if (!ogrMultiPoint) {
continue;
}
for (int gi = 0; gi < ogrMultiPoint->getNumGeometries(); gi++) {
OGRPoint *ogrPoint =
dynamic_cast<OGRPoint *>(ogrMultiPoint->getGeometryRef(gi));
if (ogrPoint) {
vertexList.emplace_back(ogrPoint->getX(), ogrPoint->getY(), 0);
}
}
break;
}
default: {
printf("未处理的特征类型\n");
break;
}
}
OGRFeature::DestroyFeature(poFeature);
}
}
GDALClose(poDS);
poDS = nullptr;
return true;
}
bool WriteVector(const Delaunay &dt) {
string dstFile = "Data/Out.shp";
GDALDriver *driver =
GetGDALDriverManager()->GetDriverByName("ESRI Shapefile");
if (!driver) {
printf("Get Driver ESRI Shapefile Error!\n");
return false;
}
GDALDataset *dataset =
driver->Create(dstFile.c_str(), 0, 0, 0, GDT_Unknown, NULL);
OGRLayer *poLayer = dataset->CreateLayer("tin", NULL, wkbPolygon, NULL);
//创建面要素
for (const auto &f : dt.finite_face_handles()) {
OGRFeature *poFeature = new OGRFeature(poLayer->GetLayerDefn());
OGRLinearRing ogrring;
for (int i = 0; i < 3; i++) {
ogrring.setPoint(i, f->vertex(i)->point().x(), f->vertex(i)->point().y());
}
ogrring.closeRings();
OGRPolygon polygon;
polygon.addRing(&ogrring);
poFeature->SetGeometry(&polygon);
if (poLayer->CreateFeature(poFeature) != OGRERR_NONE) {
printf("Failed to create feature in shapefile.\n");
return false;
}
}
//释放
GDALClose(dataset);
dataset = nullptr;
return true;
}
int main() {
GDALAllRegister();
CPLSetConfigOption("GDAL_FILENAME_IS_UTF8", "NO"); //支持中文路径
CPLSetConfigOption("SHAPE_ENCODING", ""); //解决中文乱码问题
vector<Point> vertexList;
ReadVector(vertexList);
Delaunay dt(vertexList.begin(), vertexList.end());
WriteVector(dt);
return 0;
}
这里我们先从一个矢量中读取了离散点集,在QGIS中显示如下图4.21所示:
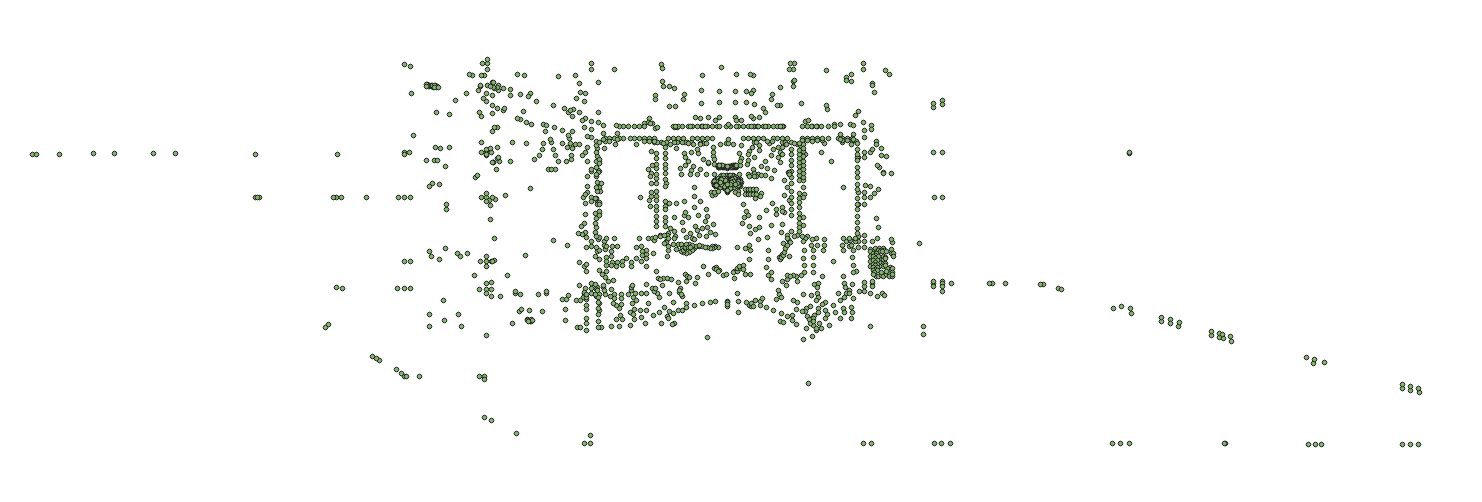
在程序最后,将生成的Delaunay三角网输出成另外一个矢量文件,在QGIS中显示如下图4.22所示:
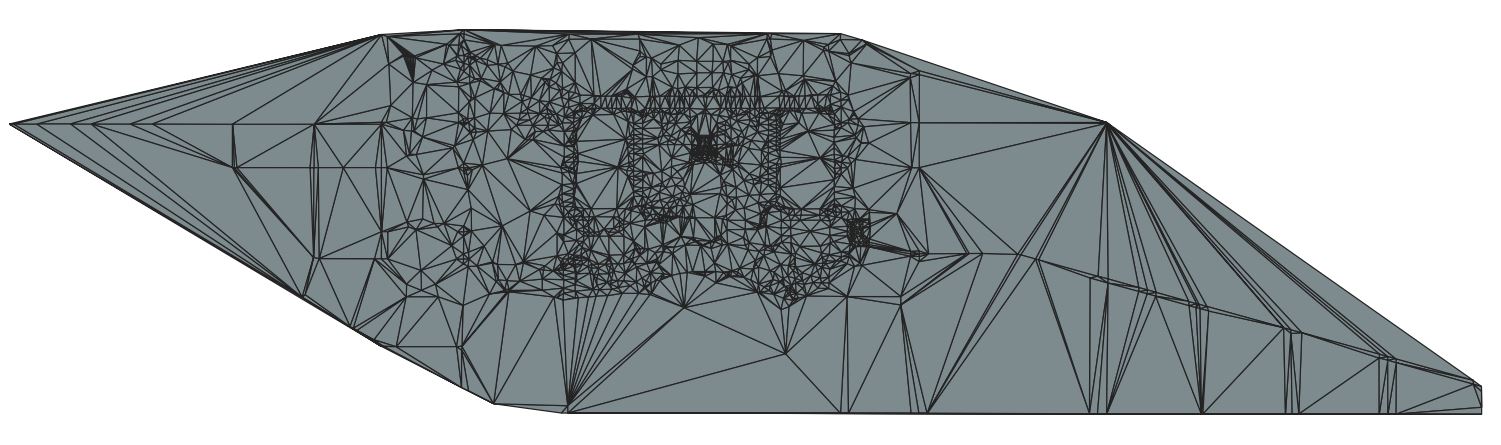
读取和写出比较好理解,关键是调用CGAL进行构建Delaunay三角网,其实相当简短:
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Projection_traits_xy_3<K> Gt;
typedef CGAL::Delaunay_triangulation_2<Gt> Delaunay;
typedef K::Point_3 Point;
int main() {
{
//...
vector<Point> vertexList;
//...
Delaunay dt(vertexList.begin(), vertexList.end());
//...
}
CGAL大量应用了C++的模板(泛型)技术,因而使用的接口比较抽象可能难以理解,这里可以解释一下CGAL的设计逻辑。学过任何一门编程语言的都知道,浮点型数值的相等判断不能直接使用相等运算符;正确的做法是使用两者相减的绝对值与容差进行判断,因为计算机表达的浮点型是个近似值。计算几何的核心问题正在于此,内置数据类型的精度是有限的,处理容差是非常麻烦的事情。所以数值需要更为精确的表达,比如0.5就应该就是0.5,不能是0.49999999。因此CGAL确定了一个Kernel(核)的概念,通过模板来控制不同精度。
这里的typedef CGAL::Exact_predicates_inexact_constructions_kernel K;表示精确谓词,但不精确构造的内核。predicates(谓词)表示一个操作;(constructions)构造意味着会有新的数值对象作为结果,如果算法是一个不进行构造的算法中,就可以使用精确谓词但不精确构造的内核。比如这里的构建Delaunay三角网,并没有新的点对象生成出来,只是对点集进行了组织,点还是原来哪些点,并没有变化。
另外,typedef K::Point_3 Point;表示我们使用该精度下的内置三维点类型。但是另外一个问题在于,如果我们需要定义三个维度中的哪两个维度数值参与构网计算,或者使用自定义数据结构该怎么办呢?所以可以传入Traits类型,这其实是C++的模板中的traits技术,描述了传入数据的数值特性:比如类型,排序,方向测试或者相等判断等。每个Kernel中都有定义好的Traits类型,这里使用的就是typedef CGAL::Projection_traits_xy_3<K> Gt;,使用点的xy值参与构网计算。最后将该类型作为模板参数传入到Delaunay三角网构建类中:typedef CGAL::Delaunay_triangulation_2<Gt> Delaunay;。
上述的解析读者如果没有一定的C++模板知识的基础,肯定看的云里雾里。其实不要紧,笔者也只是希望大家能够理解CGAL如此设计接口的内在逻辑,并不是故意设计的如此抽象和繁琐,而是希望最大程度的保证精度和性能。更多更具体的解析,读者可以参看CGAL文档。对C++模板知识不熟悉的初学者,建议直接参考文档中的给出的实例,在实际使用过程中逐渐增加自己的认识。