给定循环单调非递减列表中的一个点，写一个函数向这个列表中插入一个新元素 insertVal ，使这个列表仍然是循环升序的
给定的可以是这个列表中任意一个顶点的指针，并不一定是这个列表中最小元素的指针
如果有多个满足条件的插入位置，可以选择任意一个位置插入新的值，插入后整个列表仍然保持有序
如果列表为空（给定的节点是 null），需要创建一个循环有序列表并返回这个节点。否则。请返回原先给定的节点
示例 1：

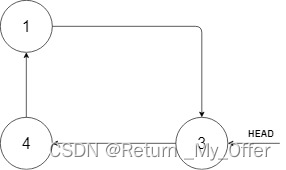
输入：head = [3,4,1], insertVal = 2
输出：[3,4,1,2]
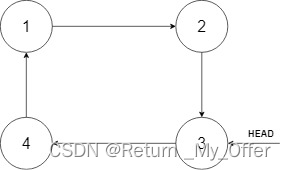
解释：在上图中，有一个包含三个元素的循环有序列表，你获得值为 3 的节点的指针，我们需要向表中插入元素 2 。新插入的节点应该在 1 和 3 之间，插入之后，整个列表如上图所示，最后返回节点 3

示例 2：
输入：head = [], insertVal = 1
输出：[1]
解释：列表为空（给定的节点是 null），创建一个循环有序列表并返回这个节点
示例 3：
输入：head = [1], insertVal = 0
输出：[1,0]

方法：一次遍历

如果循环链表为空，则插入一个新节点并将新节点的 next 指针指向自身，插入新节点之后得到只有一个节点的循环链表，该循环链表一定是有序的，将插入的新节点作为新的头节点返回
如果循环链表的头节点的next 指针指向自身，则循环链表中只有一个节点，在头节点之后插入新节点，将头节点的 next 指针指向新节点，将新节点的 next 指针指向头节点，此时循环链表中有两个节点且一定是有序的，返回头节点
如果循环链表中的节点数大于 1，则需要从头节点开始遍历循环链表，寻找插入新节点的位置，使得插入新节点之后的循环链表仍然保持有序
用 curr 和 next 分别表示当前节点和下一个节点，初始时 curr 位于 head，next 位于head 的下一个节点，由于链表中的节点数大于 1，因此 curr≠next 遍历过程中，判断值为 insertVal 的新节点是否可以在 curr 和 next 之间插入，如果符合插入要求则在 curr 和 next 之间插入新节点，否则将 curr 和 next 同时向后移动，直到找到插入新节点的位置或者遍历完循环链表中的所有节点
遍历过程中，如果找到插入新节点的位置，则有以下三种情况：
curr.val≤insertVal≤next.val，此时新节点的值介于循环链表中的两个节点值之间，在 curr 和 next 之间插入新节点 curr.val>next.val 且 insertVal>curr.val，此时 curr 和 next 分别是循环链表中的值最大的节点和值最小的节点，insertVal 大于 curr 的节点值，因此新节点应该在 curr 的后面插入，即在 curr 和 next 之间插入新节点
curr.val>next.val 且 insertVal<next.val，此时 curr\textit{curr}curr 和 next 分别是循环链表中的值最大的节点和值最小的节点，insertVal 小于 next 的节点值，因此新节点应该在 next 的前面插入，即在 curr 和 next 之间插入新节点
如果遍历完循环链表中的所有节点之后仍然没有遇到上述三种情况，则循环链表中的所有节点值都相同，因此新节点插入循环链表中的任何位置仍可以使循环链表保持有序，此时仍可在 curr 和 next 之间插入新节点
在 curr 和 next 之间插入新节点的方法是：用 node 表示值为 insertVal 的新节点，令 curr.next\指向 node，令 node.next 指向 next，即完成插入新节点的操作

// struct Node {
//     int val;
//     struct Node* next;
// };

//#include<stdlib.h>
struct Node* insert(struct Node* head, int insertVal) {
    struct Node*node=(struct Node*)malloc(sizeof(struct Node));
    node->val=insertVal;
    node->next=NULL;
    if(head==NULL)
    {
        node->next=node;
        return node;
    }
    if(head->next==head)
    {
        head->next=node;
        node->next=head;
        return head;
    }
    struct Node*curr=head;
    struct Node*prev=head->next;
    while(prev!=head)
    {
        if(insertVal>=curr->val&&insertVal<=prev->val)
        {
            break;
        }
        if(curr->val>prev->val)
        {
            if(insertVal>curr->val||insertVal<prev->val)
            {
                break;
            }
        }
        curr=curr->next;
        prev=prev->next;
    }
    curr->next=node;
    node->next=prev;
    return head;
}