提示:努力生活,开心、快乐的一天
文章目录
- 84. 柱状图中最大的矩形
- 💡解题思路
- 🤔遇到的问题
- 💻代码实现
- 🎯题目总结
- 总结
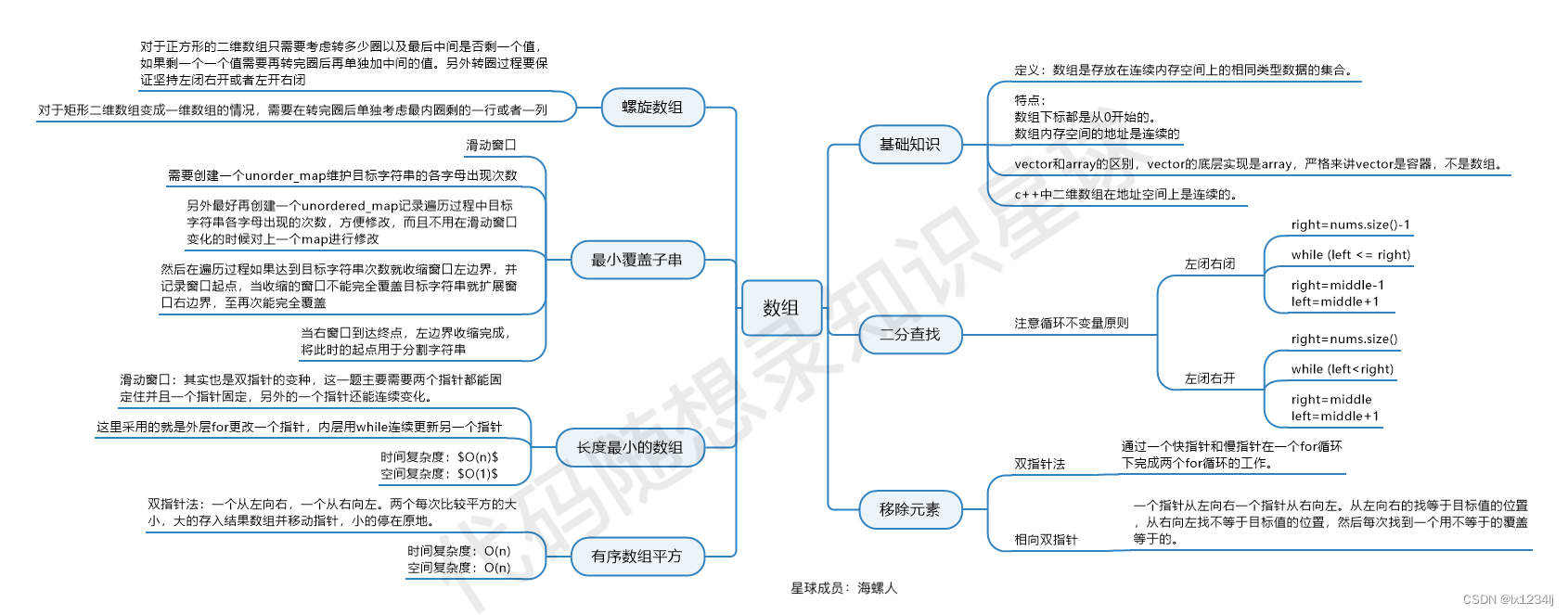
- 数组
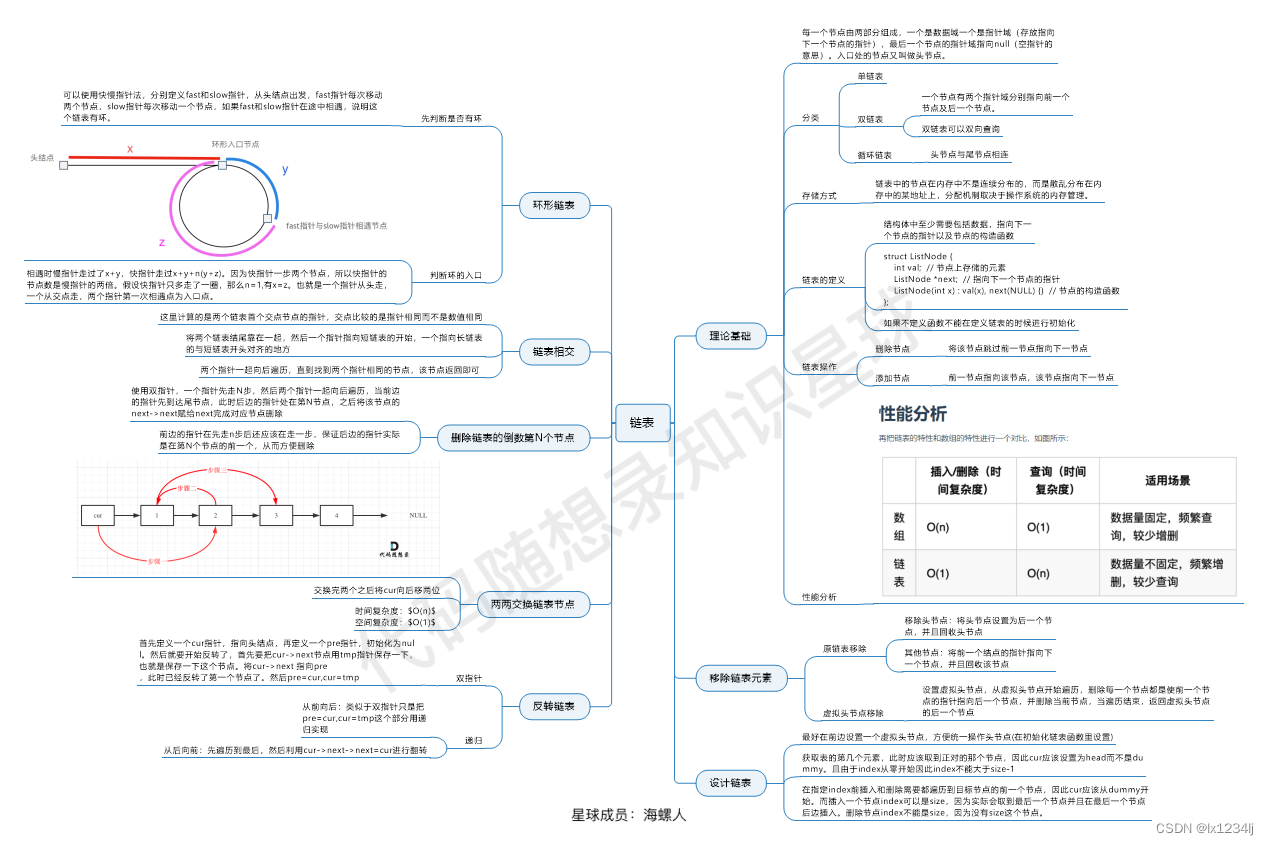
- 链表
- 哈希表
- 数组作为哈希表
- set作为哈希表
- map作为哈希表
- 字符串
- 要不要使用库函数
- 双指针法
- 反转系列
- KMP
- 双指针
- 数组篇
- 字符串篇
- 链表篇
- N数之和篇
- 栈与队列
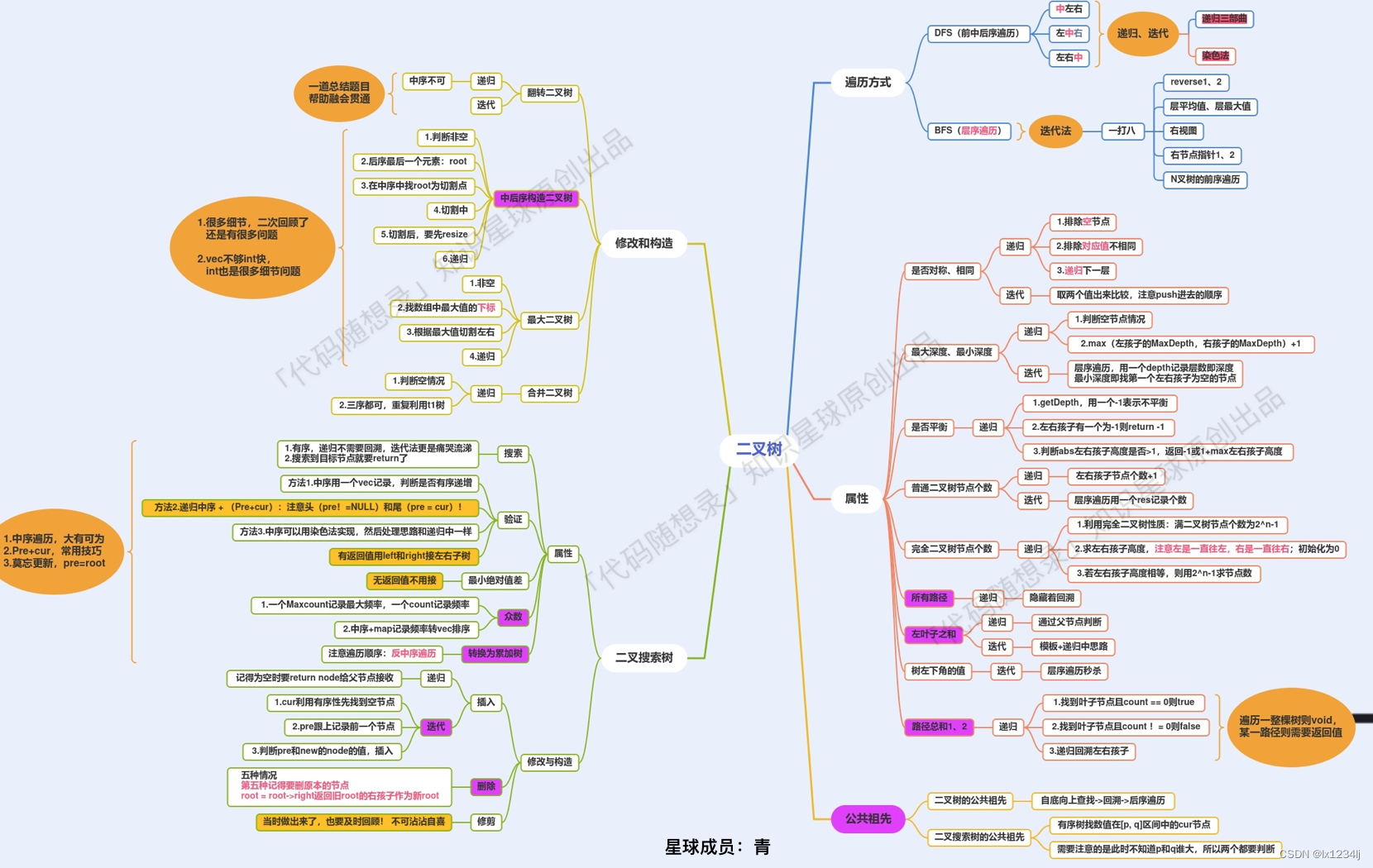
- 二叉树
- 回溯
- 回溯
- 动态规划
84. 柱状图中最大的矩形
题目链接:84. 柱状图中最大的矩形
💡解题思路
- 本地单调栈的解法和接雨水的题目是遥相呼应的。
42.接雨水 (opens new window)是找每个柱子左右两边第一个大于该柱子高度的柱子,而本题是找每个柱子左右两边第一个小于该柱子的柱子。这里就涉及到了单调栈很重要的性质,就是单调栈里的顺序,是从小到大还是从大到小。
在题解42. 接雨水 (opens new window)中我讲解了接雨水的单调栈从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子,所以从栈头(元素从栈头弹出)到栈底的顺序应该是从大到小的顺序!
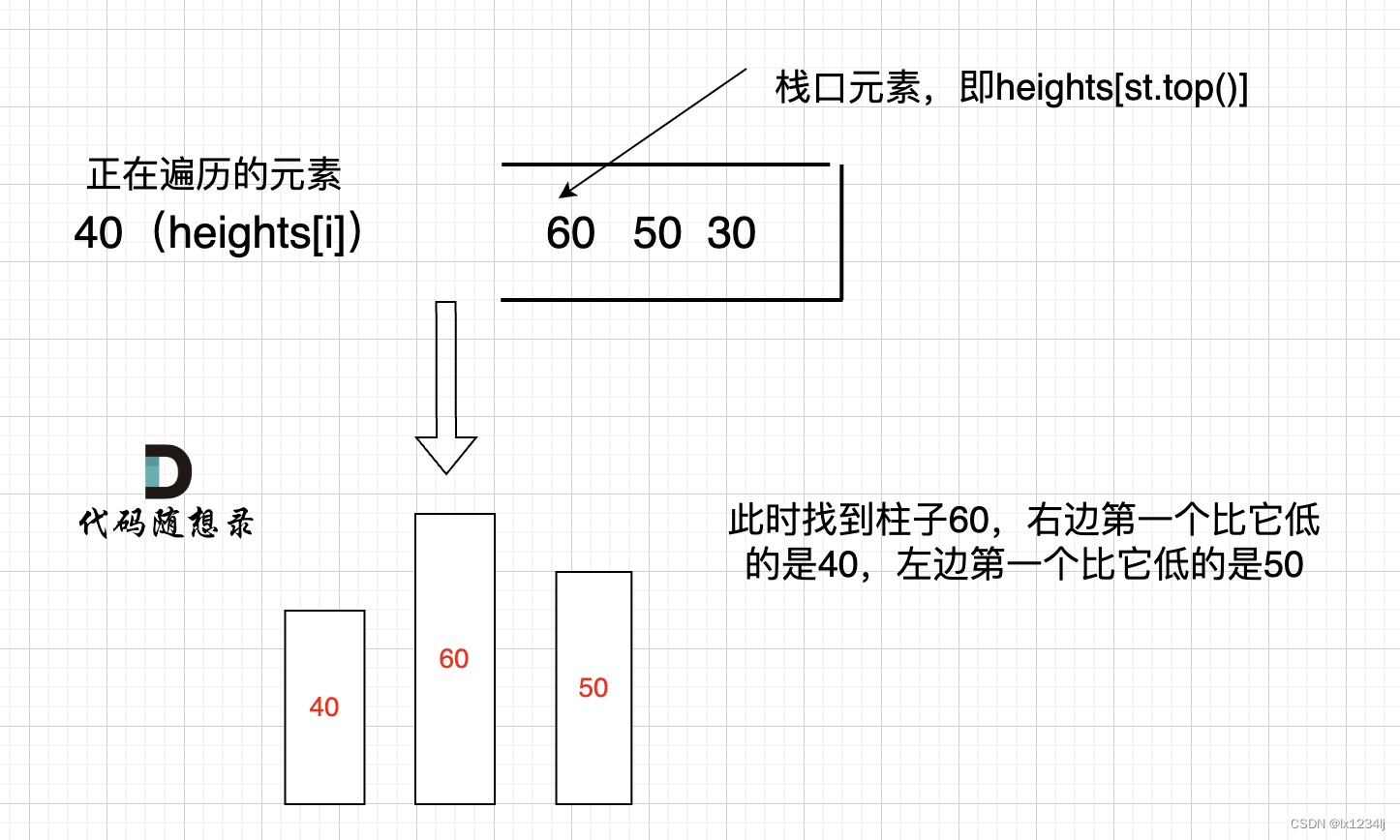
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
所以本题单调栈的顺序正好与接雨水反过来。
其实就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度 - 主要就是分析清楚如下三种情况:
情况一:当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
情况二:当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
情况三:当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
🤔遇到的问题
💻代码实现
var largestRectangleArea = function(heights) {
let maxArea = 0;
const stack = [];
heights = [0,...heights,0]; // 数组头部加入元素0 数组尾部加入元素0
for(let i = 0; i < heights.length; i++){ // 只用考虑情况一 当前遍历的元素heights[i]小于栈顶元素heights[stack[stack.length-1]]]的情况
while(heights[i] < heights[stack[stack.length-1]]){// 当前bar比栈顶bar矮
const stackTopIndex = stack.pop();// 栈顶元素出栈,并保存栈顶bar的索引
let w = i - stack[stack.length -1] - 1;
let h = heights[stackTopIndex]
// 计算面积,并取最大面积
maxArea = Math.max(maxArea, w * h);
}
stack.push(i);// 当前bar比栈顶bar高了,入栈
}
return maxArea;
};
🎯题目总结
height数组上后,都加了一个元素0, 为什么这么做呢?
首先来说末尾为什么要加元素0?
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图: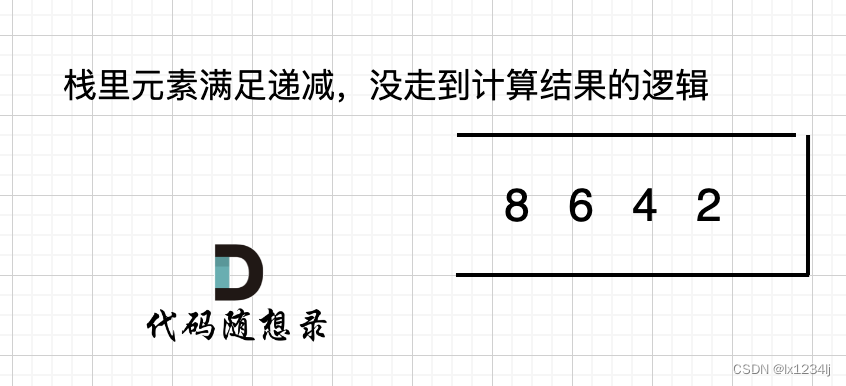
那么结尾加一个0,就会让栈里的所有元素,走到情况三的逻辑。
开头为什么要加元素0?
如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时我们得到 mid(8),rigt(6),但是得不到 left。
(mid、left,right 都是对应版本一里的逻辑)
因为 将 8 弹出之后,栈里没有元素了,那么为了避免空栈取值,直接跳过了计算结果的逻辑。
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 8 进行比较,周而复始,那么计算的最后结果resutl就是0。 如图所示: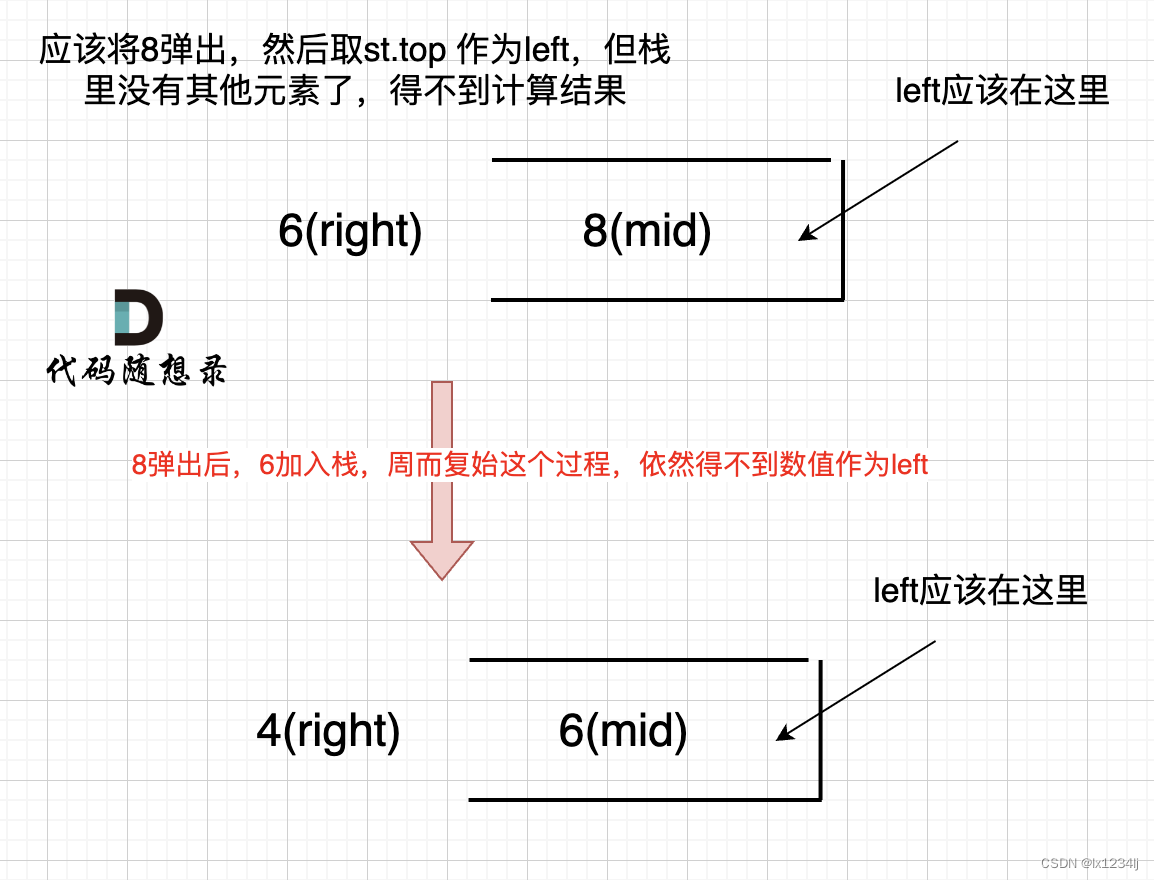
所以我们需要在 height数组前后各加一个元素0。
总结
总结多引用代码随想录中的图片参考
数组
链表
哈希表
常见的三种哈希结构:
- 数组
- set(集合)
- map(映射)
数组作为哈希表
使用map确实可以,但使用map的空间消耗要比数组大一些,因为map要维护红黑树或者符号表,而且还要做哈希函数的运算。所以数组更加简单直接有效!
set作为哈希表
主要因为如下两点:
- 数组的大小是有限的,受到系统栈空间(不是数据结构的栈)的限制。
- 如果数组空间够大,但哈希值比较少、特别分散、跨度非常大,使用数组就造成空间的极大浪费。
map作为哈希表
使用数组和set来做哈希法的局限:
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
map是一种<key, value>的结构,本题可以用key保存数值,用value在保存数值所在的下标。所以使用map最为合适。
字符串
要不要使用库函数
如果题目关键的部分直接用库函数就可以解决,建议不要使用库函数。
双指针法
双指针法在数组,链表和字符串中很常用。
其实很多数组填充类的问题,都可以先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
反转系列
当需要固定规律一段一段去处理字符串的时候,要想想在在for循环的表达式上做做文章。
先整体反转再局部反转或者先局部反转再整体反转
KMP
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
KMP的精髓所在就是前缀表,在KMP精讲 (opens new window)中提到了,什么是KMP,什么是前缀表,以及为什么要用前缀表。
前缀表:起始位置到下标i之前(包括i)的子串中,有多大长度的相同前缀后缀。
那么使用KMP可以解决两类经典问题:
匹配问题:28. 实现 strStr()(opens new window)
重复子串问题:459.重复的子字符串(opens new window)
前缀:指不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀:指不包含第一个字符的所有以最后一个字符结尾的连续子串。
然后针对前缀表到底要不要减一,这其实是不同KMP实现的方式,我们在KMP精讲 (opens new window)中针对之前两个问题,分别给出了两个不同版本的的KMP实现。
其中主要理解j=next[x]这一步最为关键!
双指针
数组篇
通过两个指针在一个for循环下完成两个for循环的工作
字符串篇
使用双指针法,定义两个指针(也可以说是索引下标),一个从字符串前面,一个从字符串后面,两个指针同时向中间移动,并交换元素。,时间复杂度是O(n)。
其实很多数组(字符串)填充类的问题,都可以先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
在删除冗余空格的过程中,如果不注意代码效率,很容易写成了O(n^2)的时间复杂度。其实使用双指针法O(n)就可以搞定。
链表篇
使用双指针法来翻转链表,只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表。
使用快慢指针(双指针法),分别定义 fast 和 slow指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环。
N数之和篇
通过前后两个指针不算向中间逼近,在一个for循环下完成两个for循环的工作。
栈与队列
在栈与队列系列中,我们强调栈与队列的基础,也是很多同学容易忽视的点。
使用抽象程度越高的语言,越容易忽视其底层实现,而C++相对来说是比较接近底层的语言。
我们用栈实现队列,用队列实现栈来掌握的栈与队列的基本操作。
接着,通过括号匹配问题、字符串去重问题、逆波兰表达式问题来系统讲解了栈在系统中的应用,以及使用技巧。
通过求滑动窗口最大值,以及前K个高频元素介绍了两种队列:单调队列和优先级队列,这是特殊场景解决问题的利器,是一定要掌握的。
二叉树
涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
注意在普通二叉树的属性中,我用的是一般为后序,例如单纯求深度就用前序,二叉树:找所有路径 (opens new window)也用了前序,这是为了方便让父节点指向子节点。
所以求普通二叉树的属性还是要具体问题具体分析
回溯
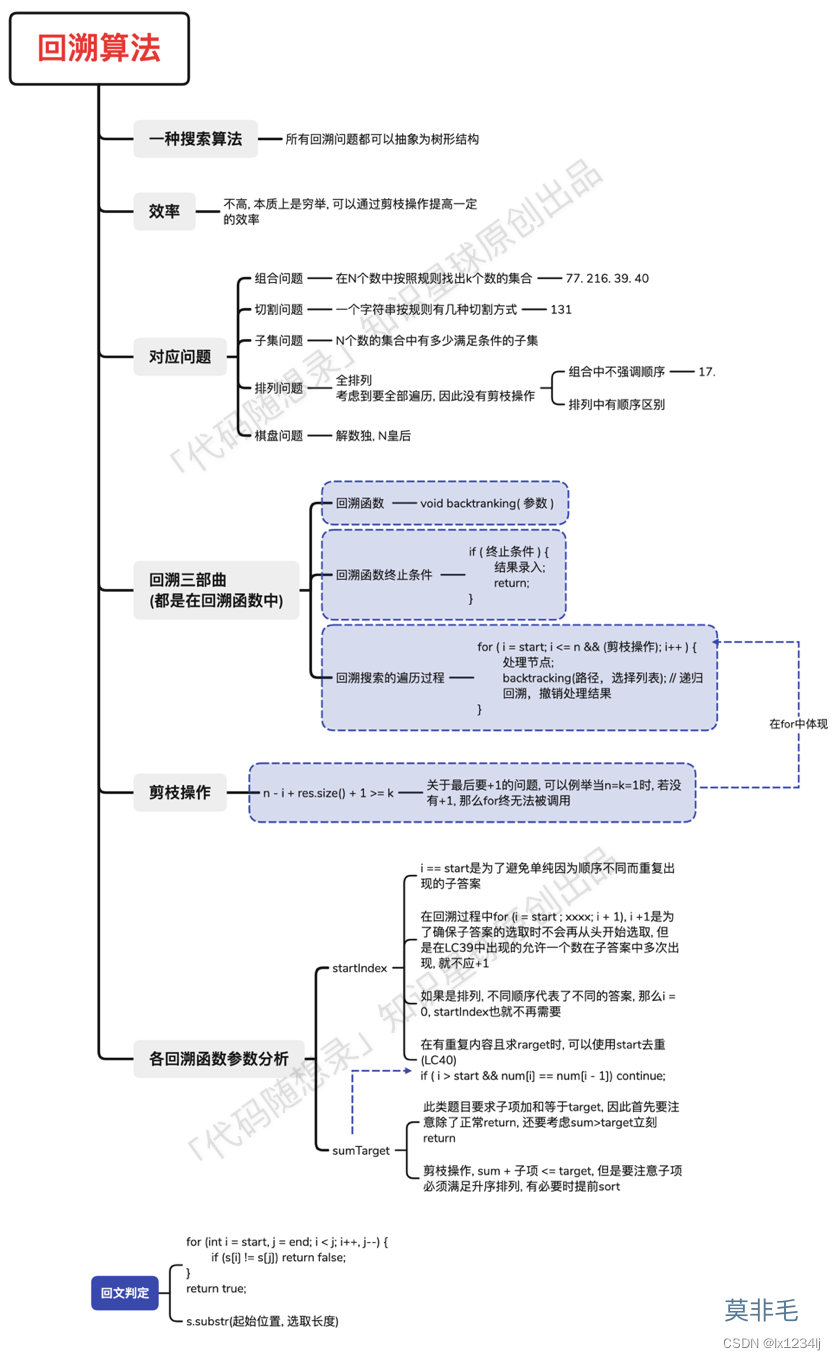
回溯
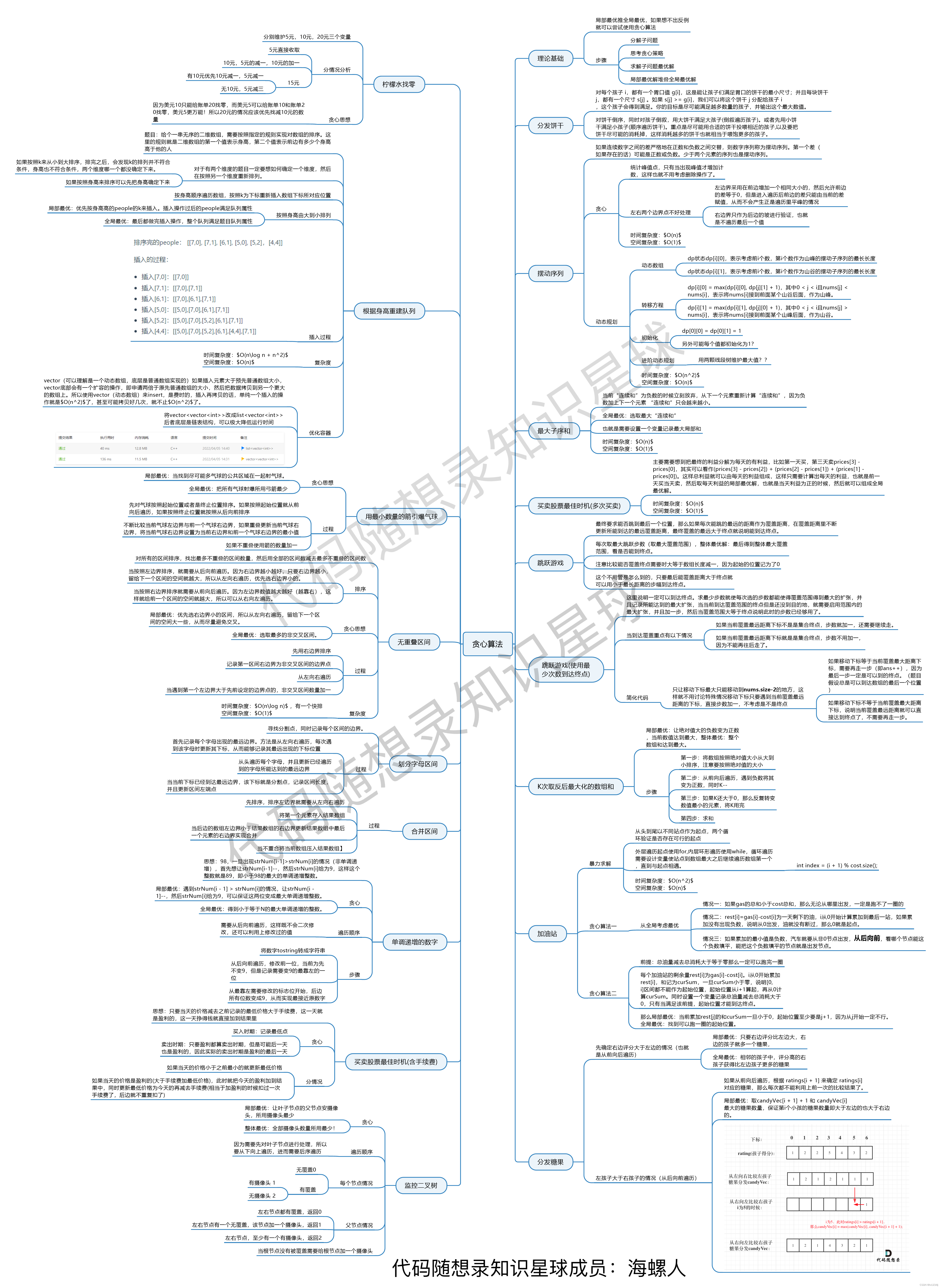
动态规划
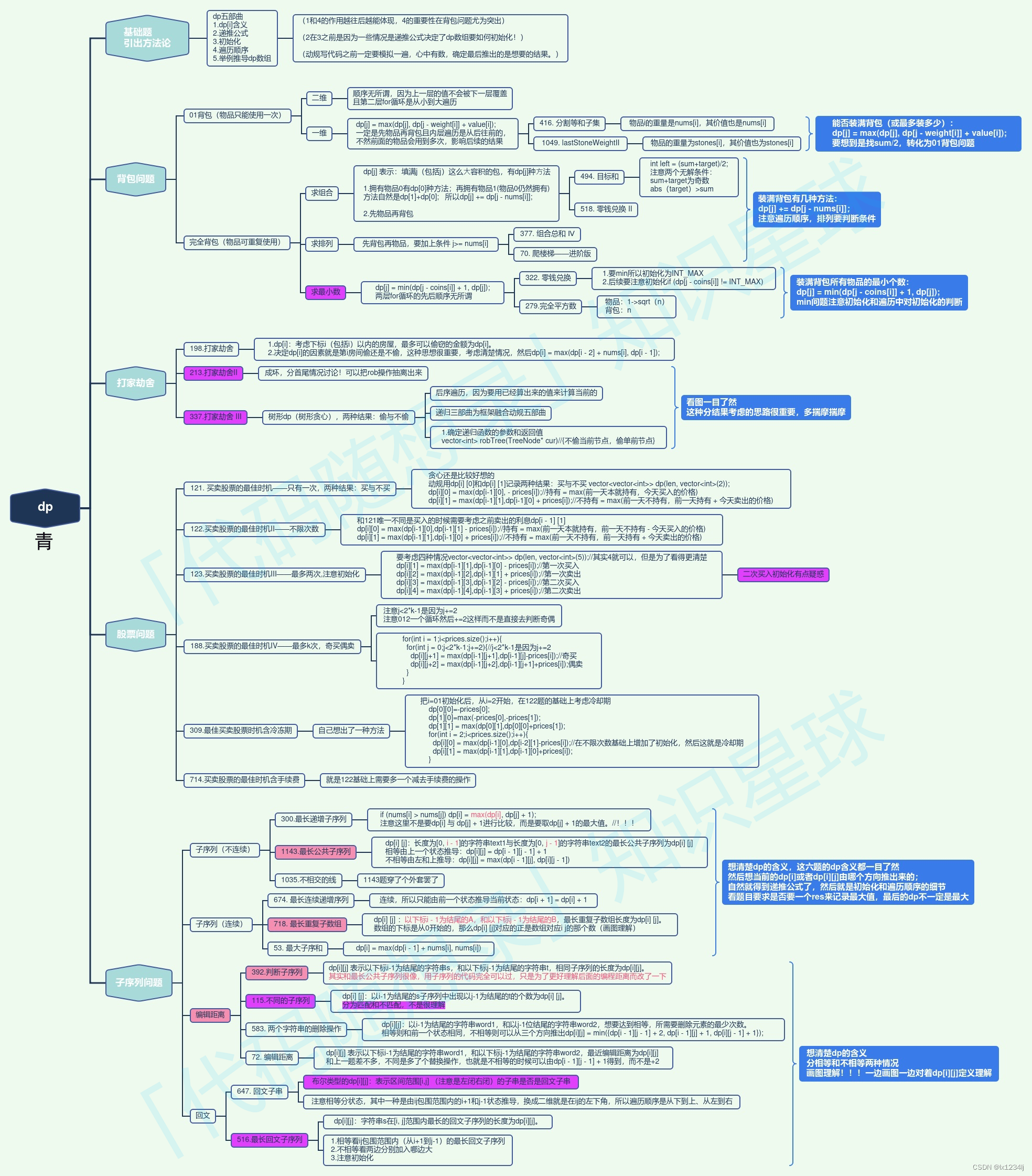




![[ThinkPHP]The namespace “work“ is ambiguous (worker, workflow)](https://img-blog.csdnimg.cn/5518bfb71edc403083b4ceede56a736e.png)