本期文章将讲述常用智能优化算法改进策略---飞行游走篇,一共包含五种常见的改进策略:
①莱维飞行,②随机游走,③螺旋飞行,④高斯随机游走,⑤三角形游走
五种策略可以方便移植到其他任何智能算法的改进中!
为了方便大家对这五种改进策略的深入了解,作者将这五种策略用在简单易懂的粒子群算法中,以此来教大家如何运用这五种策略,今后也方便大家移植到别的智能算法中。
①莱维飞行
莱维飞行具有遍历性和随机性,是一种非高斯的随机过程,它的平稳增量服从莱维稳定分布,其飞行轨迹是随机漫步的,由小步长 (短距离) 的跳跃聚集在一块,和偶尔大步长 (长距离) 的跳跃组成,两者相互交替。
莱维飞行作为改进智能优化算法非常常用的改进策略,其实非常简单就能移植到别的算法中。莱维飞行的具体公式如下:
带入到粒子群中,公式如下:
参考文献:奚金明,郑荣艳.基于自适应权重和莱维飞行的改进海鸥优化算法[J/OL].计算机系统应用:1-9[2023-10-23].DOI:10.15888/j.cnki.csa.009326.
②随机游走
随机游走策略是一种数学统计模型,可表示无规则运动所产生的运动轨迹。其主要过程为:每次随机选择一个当前解的邻域点进行比较,如果优于当前解则将该点作为新的中心。如果连续N次都找不到更优的值,则认为,最优解就在以当前最优解为中心,当前步长为半径的N维球内。此时,如果步长已经小于阈值,则结束算法;否则,令步长减半,开始新一轮游走。在迭代过程中,当达到一定条件时候,其概率分布会收敛,最终得到稳定的概率分布。
随机游走策略公式如下:
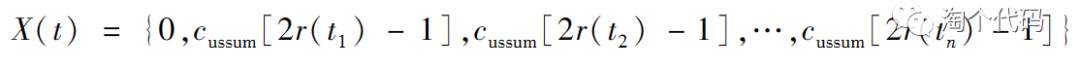
取一个随机函数r(t)如式
由于智能算法的行动轨迹有一定的范围,因而不能直接用上式来更新算法的位置。为了保证算法行走在一定的范围内,需要对其进行归一化,如下式所示。
式中:Xit为第i只麻雀在第t次迭代中的位置;αi和bi分别为第i维随机游走变量的最小值和最大值;ci和di分别为第i维随机游走变量在第t次迭代的最小值和最大值。
参考文献:马小晶,贺航,王宏伟等.基于改进麻雀搜索算法的最大指数熵分割方法[J].科学技术与工程,2023,23(16):6983-6992.
③螺旋飞行(搜索)
螺旋搜索是在鲸鱼算法中提出来的,后来被学者将这一螺旋搜索策略用于智能算法改进中。螺旋搜索可以增强算法的全局寻优能力,这不仅保证了算法的收敛速度,而且可以增加个体的多样性。螺旋搜索公式如下:
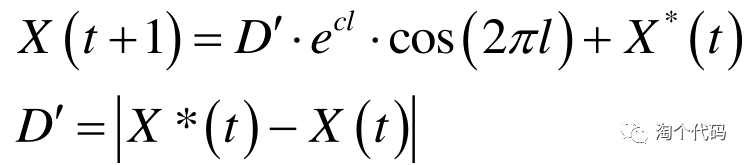
参考文献:MIRJALILI S,LEWIS A. The whale optimization algorithm[J].Advances in Engineering Software,2016,95:51一 67.
④高斯随机游走
作为随机游走模型中的经典模型,高斯随机游走模型具有优秀的开发能力。高斯随机游走策略也常常出现在智能算法的改进中,与随机游走不同,高斯随机游走在随机游走的基础上加上了高斯变异的公式,会产生一系列围绕种群最佳值变异的数列,具体的公式如下:
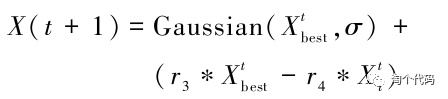
参考文献:李梓成,代永强.一种改进的鲸鱼优化算法[J].计算机技术与发展,2023,33(02):173-180.
⑤三角形游走策略
三角游走策略是智能优化算法的种群在靠近最佳位置的同时在周围进行游走。一定意义上增加了算法的局部寻优能力。公式如下:
首先,得到种群和猎物之间的距离L1,种群的游走步长范围为L2。
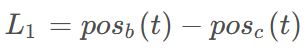
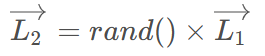
之后,根据下述公式定义行走的方向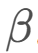 。
。
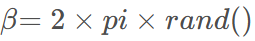
再采用下述公式求出获得种群游走后得到的位置。
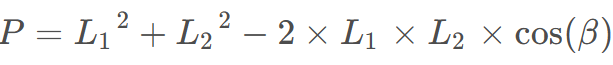
结果展示
在CEC2005函数集进行展示,设置迭代次数1000次,种群个数100个。
其中PSO为原始粒子群,Triangle_Walk_PSO为三角形游走策略,Spiral_flight_PSO为螺旋飞行策略,randwalk_PSO为随机游走策略,Levy_flight_PSO为莱维飞行策略,Gaussian_randwalk_PSO为高斯随机游走策略。
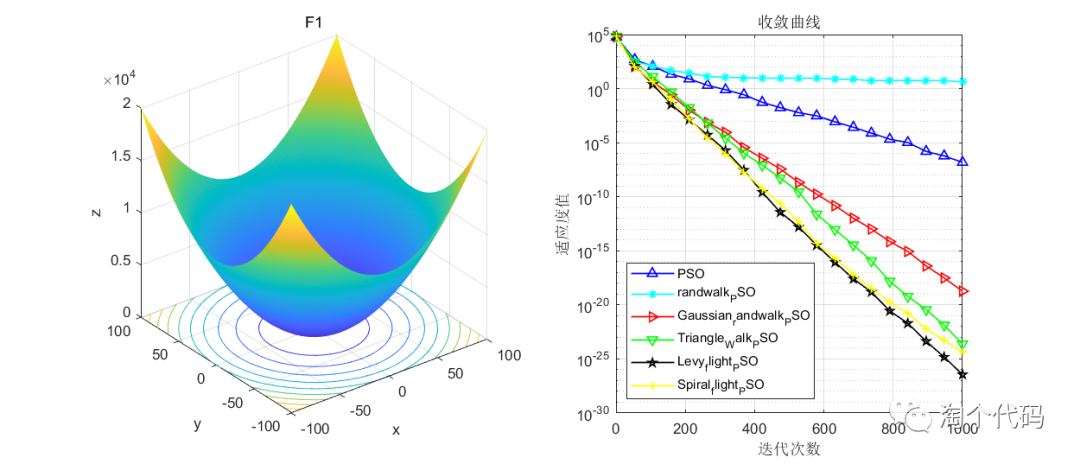
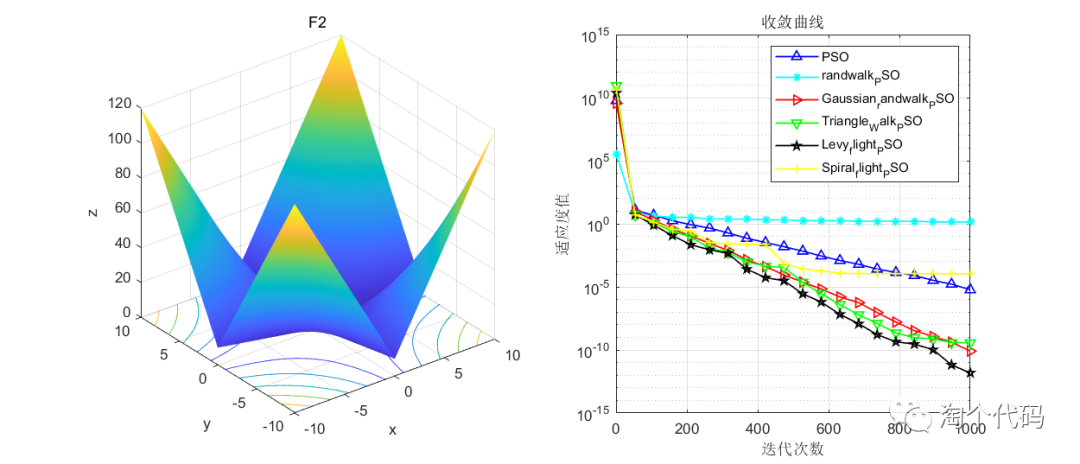
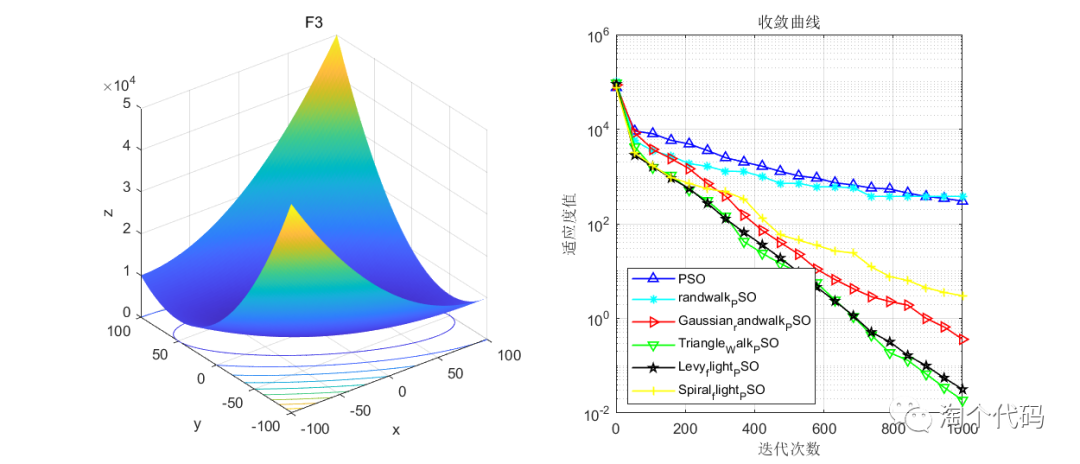
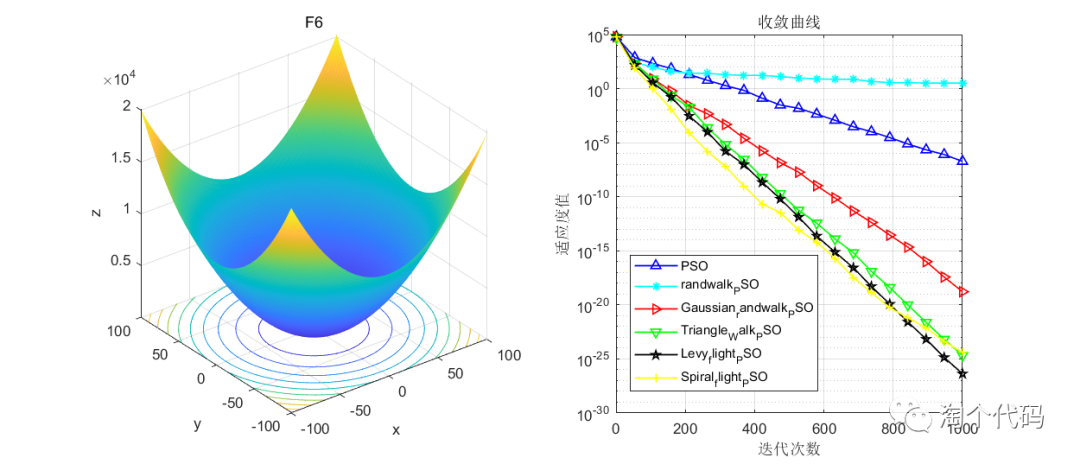
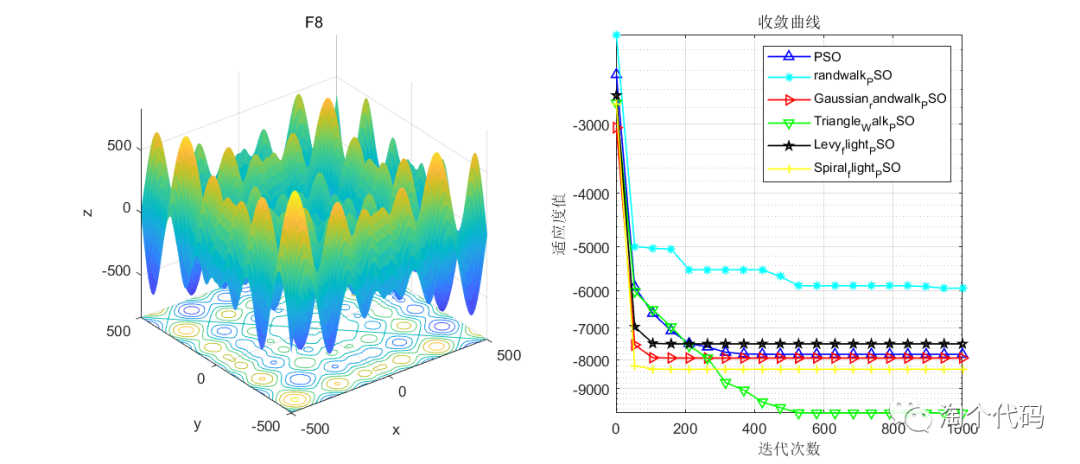
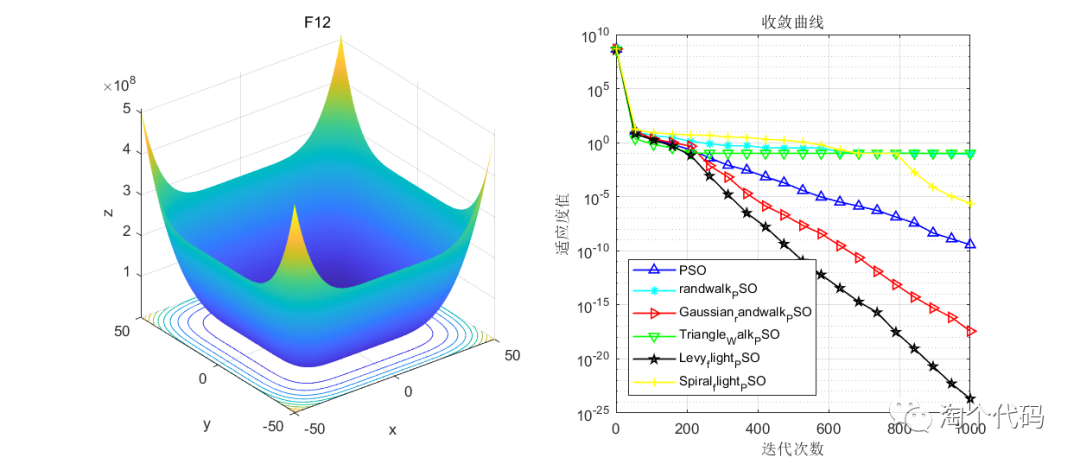
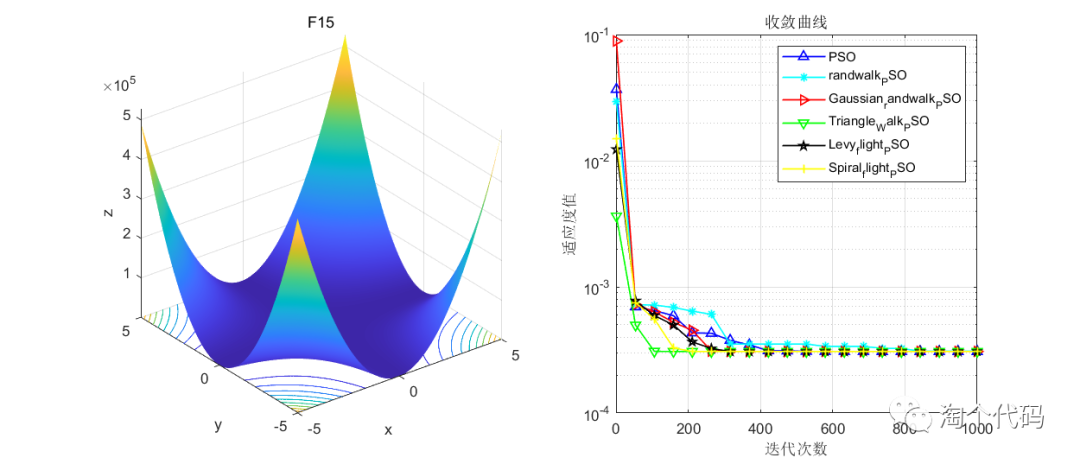
注意!本程序代码只是为了教大家如何使用这几种变异策略,如果看到改进后的算法没有原始算法效果好,请不要见怪!
友情提示:策略算法是给出了,但不是说只要你加入了策略,算法性能就一定能提升,关键还是要看这些策略的作用分别是什么,是帮助算法跳出最优解?是扩展搜索范围增强全局寻优能力?是加速算法收敛?只有明确了策略的功能和自己要改进算法的弊端,有效结合,才能提升自己的算法性能。要分析其原理并不断进行尝试!
代码展示
%% 淘个代码 %%
% 2023/10/23 %
%微信公众号搜索:淘个代码,获取更多免费代码
%禁止倒卖转售,违者必究!!!!!
%唯一官方店铺:https://mbd.pub/o/author-amqYmHBs/work,其他途径都是骗子!
%%
clear
clc
close all
number='F8'; %选定优化函数,自行替换:F1~F23
[lb,ub,dim,fobj]=CEC2005(number); % [lb,ub,D,y]:下界、上界、维度、目标函数表达式
SearchAgents=100; % population members
Max_iterations=1000; % maximum number of iteration
%% 调用PSO算法
[fMin , bestX, PSO_Convergence_curve ] = PSO(SearchAgents, Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by PSO for ' [num2str(number)],' is : ', num2str(fMin)]);
fprintf ('Best solution obtained by PSO: %s\n', num2str(bestX,'%e '));
%% 调用随机游走的PSO
[Best_score,Best_pos,randwalk_PSO_curve]=randwalk_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj); % Calculating the solution of the given problem using randwalk_PSO
display(['The best optimal value of the objective funciton found by randwalk_PSO for ' [num2str(number)],' is : ', num2str(Best_score)]);
fprintf ('Best solution obtained by randwalk_PSO: %s\n', num2str(Best_pos,'%e '));
%% 调用高斯随机游走的PSO算法
[Alpha_score,Alpha_pos,Gaussian_randwalk_PSO_Convergence_curve]=Gaussian_randwalk_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Gaussian_randwalk_PSO for ' [num2str(number)],' is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Gaussian_randwalk_PSO: %s\n', num2str(Alpha_pos,'%e '));
%% 调用莱维飞行的PSO算法
[Alpha_score,Alpha_pos,Levy_flight_PSO_Convergence_curve]=Levy_flight_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Levy_flight_PSO for ' [num2str(number)],' is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Levy_flight_PSO: %s\n', num2str(Alpha_pos,'%e '));
%% 调用三角形游走的PSO算法
[Alpha_score,Alpha_pos,Triangle_Walk_PSO_Convergence_curve]=Triangle_Walk_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Triangle_Walk_PSO for ' [num2str(number)],' is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Triangle_Walk_PSO: %s\n', num2str(Alpha_pos,'%e '));
%% 调用螺旋飞行的PSO算法
[Alpha_score,Alpha_pos,Spiral_flight_PSO_Convergence_curve]=Spiral_flight_PSO(SearchAgents,Max_iterations,lb,ub,dim,fobj);
display(['The best optimal value of the objective funciton found by Spiral_flight_PSO for ' [num2str(number)],' is : ', num2str(Alpha_score)]);
fprintf ('Best solution obtained by Spiral_flight_PSO: %s\n', num2str(Alpha_pos,'%e '));
%% Figure
figure1 = figure('Color',[1 1 1]);
G1=subplot(1,2,1,'Parent',figure1);
func_plot(number)
title(number)
xlabel('x')
ylabel('y')
zlabel('z')
subplot(1,2,2)
G2=subplot(1,2,2,'Parent',figure1);
CNT=20;
k=round(linspace(1,Max_iterations,CNT)); %随机选CNT个点
% 注意:如果收敛曲线画出来的点很少,随机点很稀疏,说明点取少了,这时应增加取点的数量,100、200、300等,逐渐增加
% 相反,如果收敛曲线上的随机点非常密集,说明点取多了,此时要减少取点数量
iter=1:1:Max_iterations;
if ~strcmp(number,'F16')&&~strcmp(number,'F9')&&~strcmp(number,'F11') %这里是因为这几个函数收敛太快,不适用于semilogy,直接plot
semilogy(iter(k),PSO_Convergence_curve(k),'b-^','linewidth',1);
hold on
semilogy(iter(k),randwalk_PSO_curve(k),'c-*','linewidth',1);
hold on
semilogy(iter(k),Gaussian_randwalk_PSO_Convergence_curve(k),'r->','linewidth',1);
hold on
semilogy(iter(k),Triangle_Walk_PSO_Convergence_curve(k),'g-v','linewidth',1);
hold on
semilogy(iter(k),Levy_flight_PSO_Convergence_curve(k),'k-p','linewidth',1);
hold on
semilogy(iter(k),Spiral_flight_PSO_Convergence_curve(k),'y-+','linewidth',1);
else
plot(iter(k),PSO_Convergence_curve(k),'b-^','linewidth',1);
hold on
plot(iter(k),randwalk_PSO_curve(k),'c-*','linewidth',1);
hold on
plot(iter(k),Gaussian_randwalk_PSO_Convergence_curve(k),'r->','linewidth',1);
hold on
plot(iter(k),Triangle_Walk_PSO_Convergence_curve(k),'g-v','linewidth',1);
hold on
plot(iter(k),Levy_flight_PSO_Convergence_curve(k),'k-p','linewidth',1);
hold on
plot(iter(k),Spiral_flight_PSO_Convergence_curve(k),'y-+','linewidth',1);
end
grid on;
title('收敛曲线')
xlabel('迭代次数');
ylabel('适应度值');
box on
legend('PSO','randwalk_PSO','Gaussian_randwalk_PSO','Triangle_Walk_PSO','Levy_flight_PSO','Spiral_flight_PSO')
set (gcf,'position', [300,300,1000,430])代码目录
直接运行MAIN.m脚本文件即可!
代码获取
完整代码获取方式:后台回复关键字,不区分大小写。关键字:
游走策略
或者点击下方阅读原文跳转链接,
或者复制链接跳转:https://mbd.pub/o/bread/ZZWZlJ1q
这篇的游走策略可以搭配之前推出的变异策略,一起阅读。