目录
一. 红黑树的定义
二. 红黑树的性质
三. 红黑树的插入
四. 红黑树的删除(略)
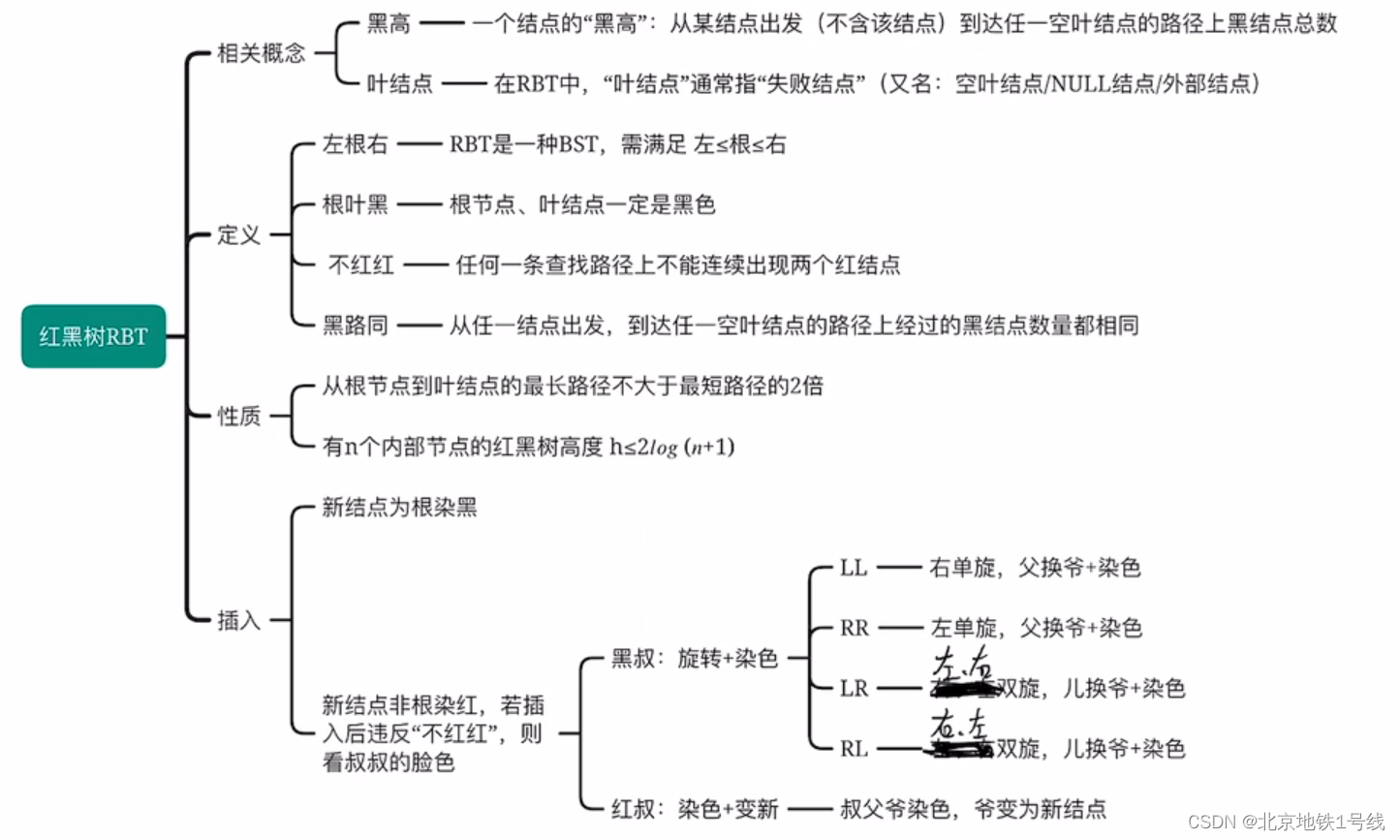
一. 红黑树的定义
红黑树是二叉排序树-左子树结点值≤根结点值≤右子树结点值。
与普通BST相比,有以下要求:
- ①每个结点或是红色,或是黑色的
- ②根节点是黑色的
- ③叶结点(外部结点、NULL结点、失败结点)均是黑色的
- ④不存在两个相邻的红结点(即红结点的父节点和孩子结点均是黑色)
- ⑤对每个结点,从该节点到任一叶结点的简单路径上,所含黑结点的数目相同
struct RBnode { //红黑树的结点定义
int key; //关键字的值
RBnode* parent; //父节点指针
RBnode* lchild; //左孩子指针
RBnode* rchild; //右孩子指针
int color; //结点颜色,如:可用0/1表示黑/红,也可使用枚举型enum表示颜色
};

结点的黑高bh:从某结点出发(不含该结点)到达任一空叶结点的路径上黑结点总数,如图:
红黑树的黑高:指根结点的黑高。

二. 红黑树的性质
性质1:从根结点到叶结点的最长路径不大于最短路径的2倍
证明:可由性质4,5推出。
性质2:有n个内部节点的红黑树高度
证明:从根到叶结点的任何一条简单路径上至少有一半是黑结点,根的黑高至少是,于是有
,得证。
性质3:根节点黑高为h的红黑树,内部结点数(关键字)至少有个

三. 红黑树的插入
先查找,确定插入位置(原理同二叉排序树),
(1)插入新结点新结点是根――染为黑色
(2)插入新结点非根结点――染为红色
2.1 若插入新结点后依然满足红黑树定义,则插入结束
2.2 若插入新结点后不满足红黑树定义,需要调整,使其重新满足红黑树定义。如何调整:看新结点叔叔(父结点的兄弟结点)的颜色:
a.叔叔结点是黑色结点:旋转+染色
(此处操作类似平衡二叉树,从爷结点开始判断类型)LL型:右单旋,父换爷+染色;RR型:左单旋,父换爷+染色;LR型:左、右双旋,儿换爷+染色;RL型:右、左双旋,儿换爷+染色;
b.叔叔结点是红色结点:染色+变新→叔父爷染色,爷变为新结点
例题:从一棵空的红黑树开始,插入:20,10,5,30,40,57,3,2,4,35,25,18,22,23,24,19,18

(1)插入20;
(2)插入10;
(3)插入5:此时10和5都是红结点,不满足要求4,5的叔叔结点是黑色,且从爷结点开始5是LL结点,因此执行“右单旋:父换爷+染色”,让父亲结点充当爷爷结点,然后改变父亲结点,爷爷结点的颜色。这里10换成黑色,20换成红色。

(4)插入30:此时20和30都是红结点,不满足要求4,30的叔叔结点5是红色,执行“染色+变新”,把叔叔,父亲,爷爷结点统统调换颜色,然后把爷爷结点10视为新插入的结点,再递归的执行一遍规则。这里10就是根结点,所以把10再染黑即可。
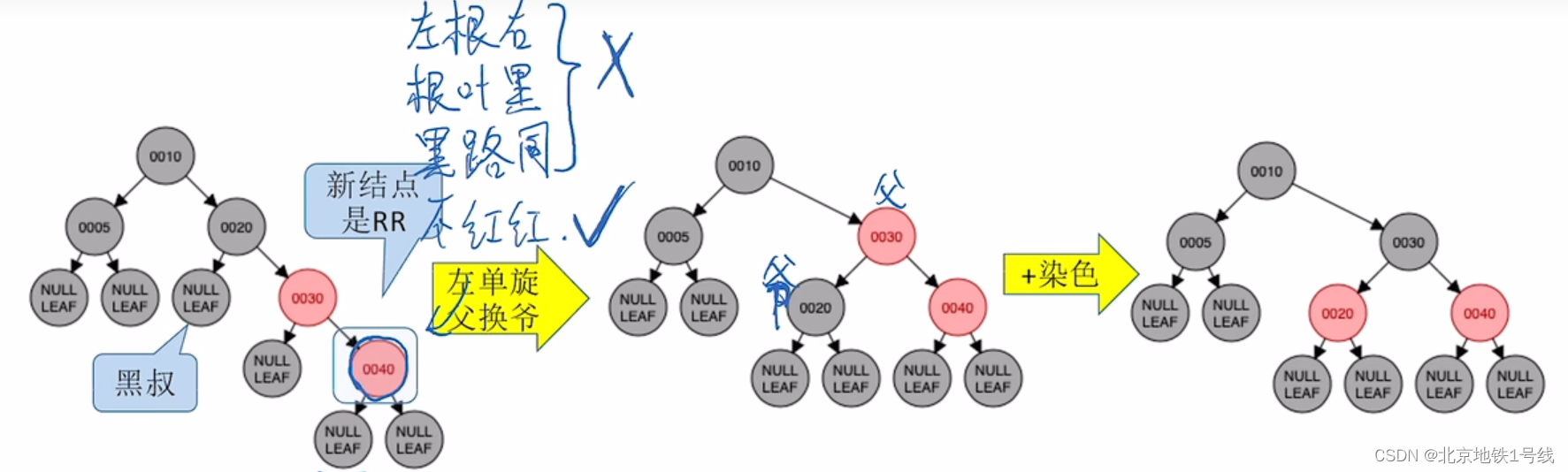
(5)插入40:此时30和40都是红结点,违反了要求4,40的叔叔结点是黑色,并且40是RR型,执行“父换爷+染色”,30充当爷结点,20就只能挂在30左子树,然后把20,30的颜色交换。

(6)插入57:此时57和40都是红结点,不满足要求4,57的叔叔结点20是红色,执行“染色+变新”,把叔叔,父亲,爷爷结点统统调换颜色,然后把爷爷结点30视为新插入的结点,再递归的执行一遍规则。这里并没有违反红黑树的要求,所以不做任何操作。

(7)插入3:没有破坏红黑树的要求4,所以不做任何操作。

(8)插入2:此时2和3都是红结点,不满足要求4,2的叔叔结点是黑色,且从爷结点开始2是LL结点,因此执行“右单旋:父换爷+染色”,让父亲结点充当爷爷结点,然后改变父亲结点,爷爷结点的颜色。这里3换成黑色,5换成红色。
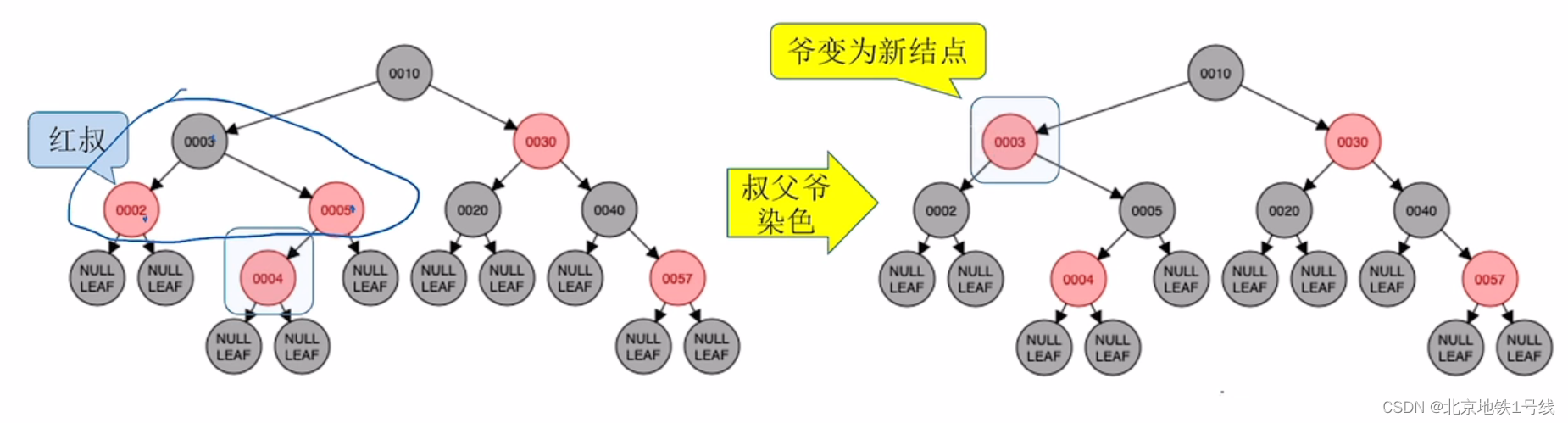
(9)插入4:此时5和4都是红结点,不满足要求4,4的叔叔结点2是红色,执行“染色+变新”,把叔叔,父亲,爷爷结点统统调换颜色,然后把爷爷结点3视为新插入的结点,再递归的执行一遍规则。这里并没有违反红黑树的要求4(对于非根结点),所以不做任何操作。


(10-12)插入35,25,18:没有破坏红黑树的要求4,所以不做任何操作。
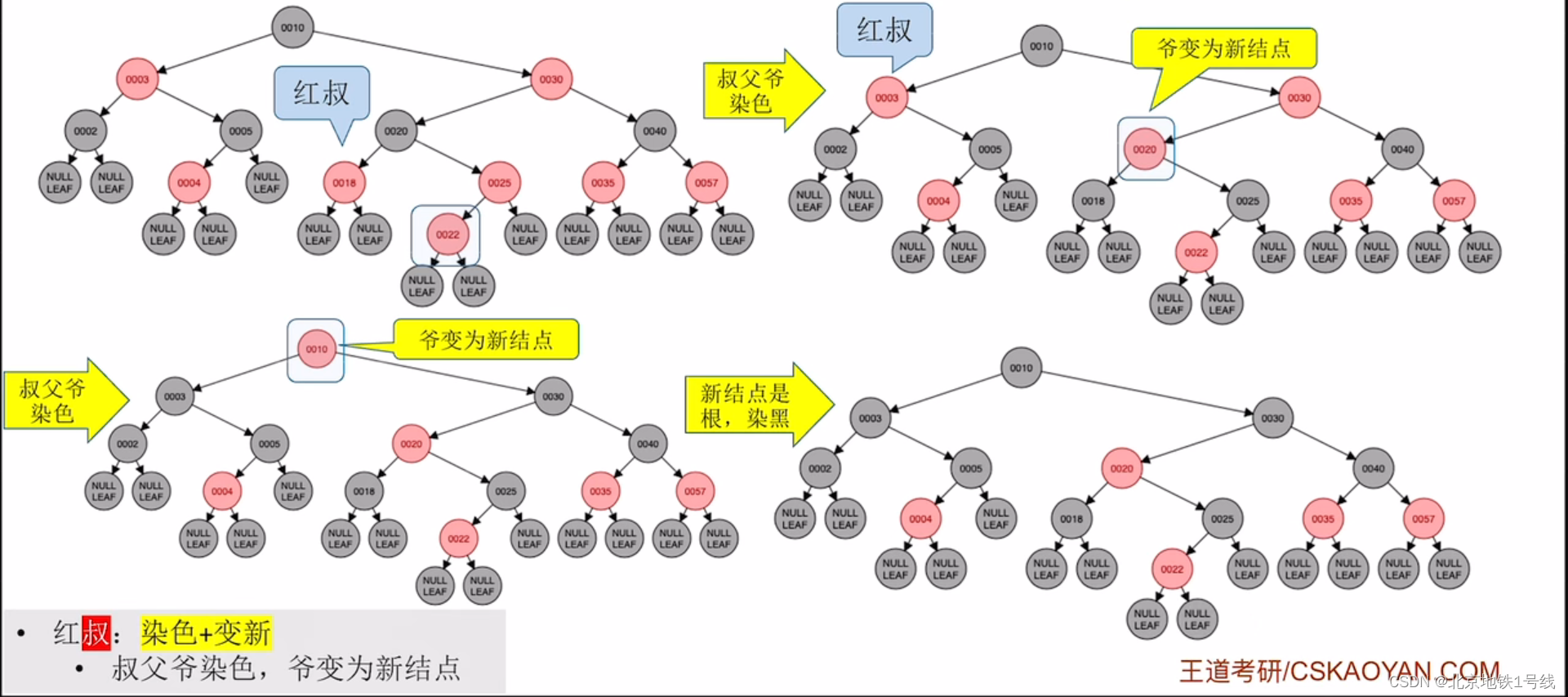
(13)插入22:此时22和25都是红结点,不满足要求4,22的叔叔结点18是红色,执行“染色+变新”,把叔叔,父亲,爷爷结点统统调换颜色,然后把爷爷结点20视为新插入的结点,再递归的执行一遍规则。这里20也违反红黑树的要求4(对于非根结点),所以再看20的叔叔结点3,它是红色。所以执行“染色+变新”,爷爷结点10视为新插入的结点,它是根结点,直接涂黑即可。
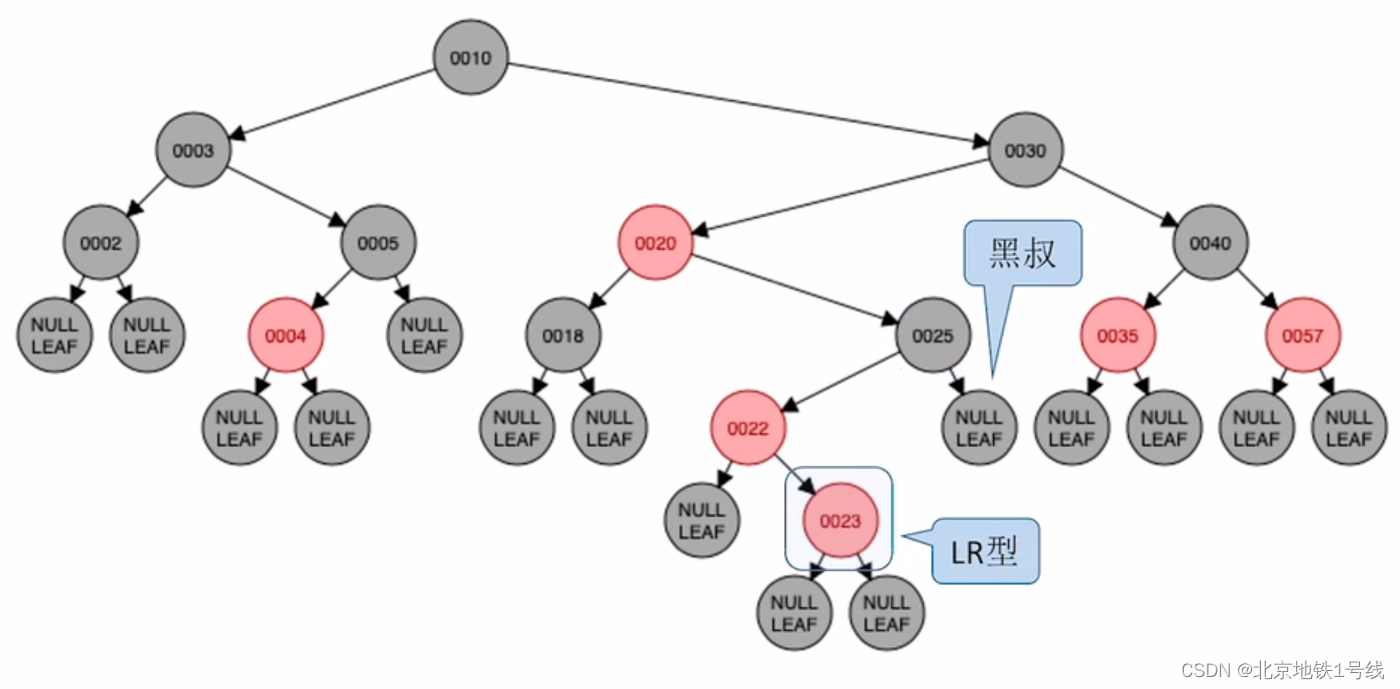
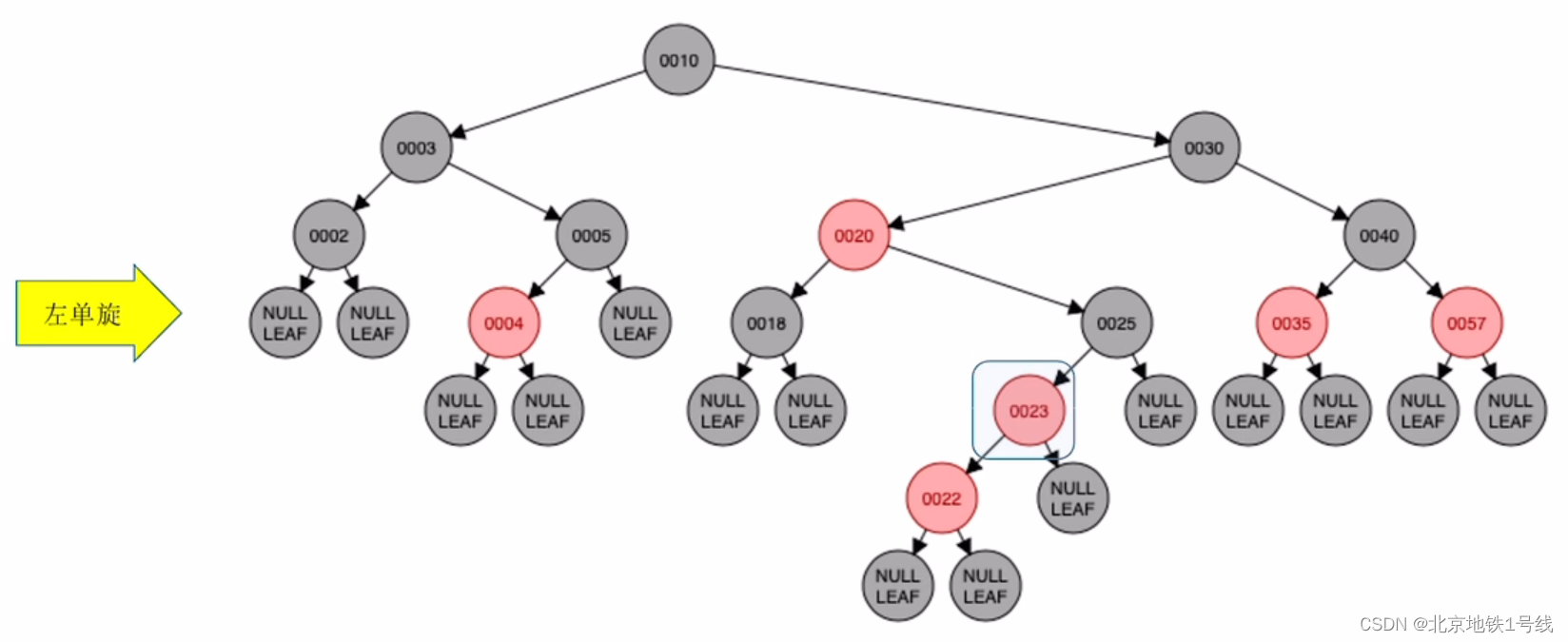
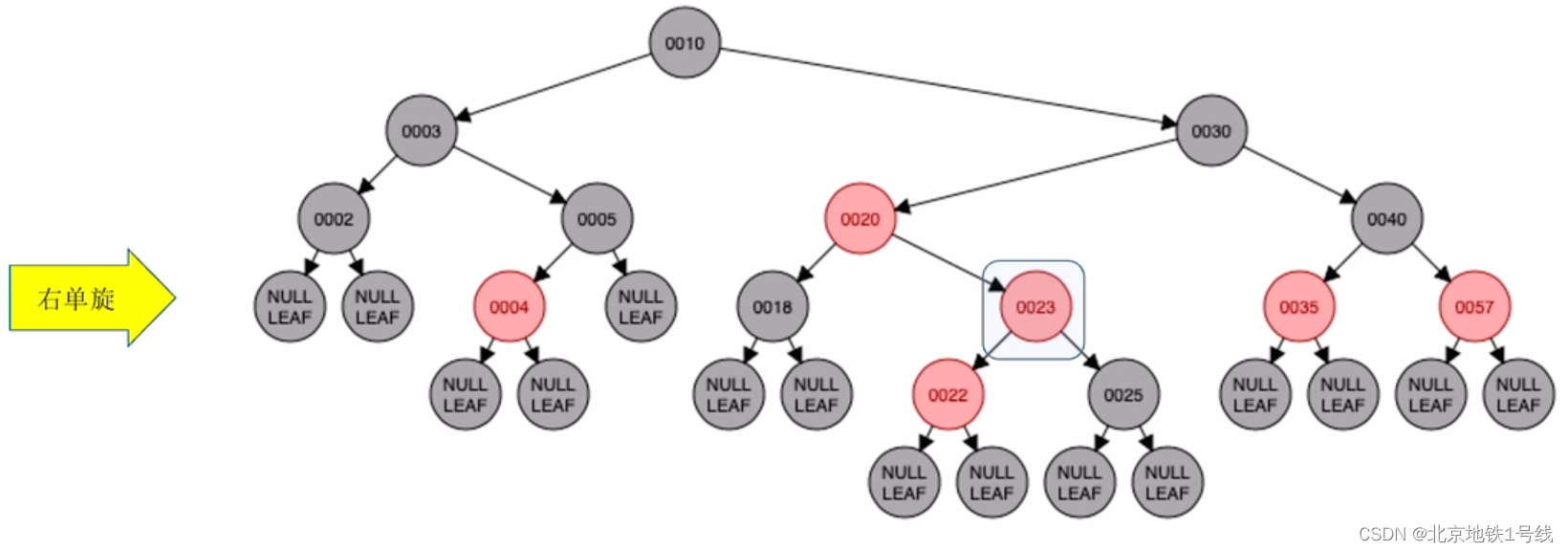
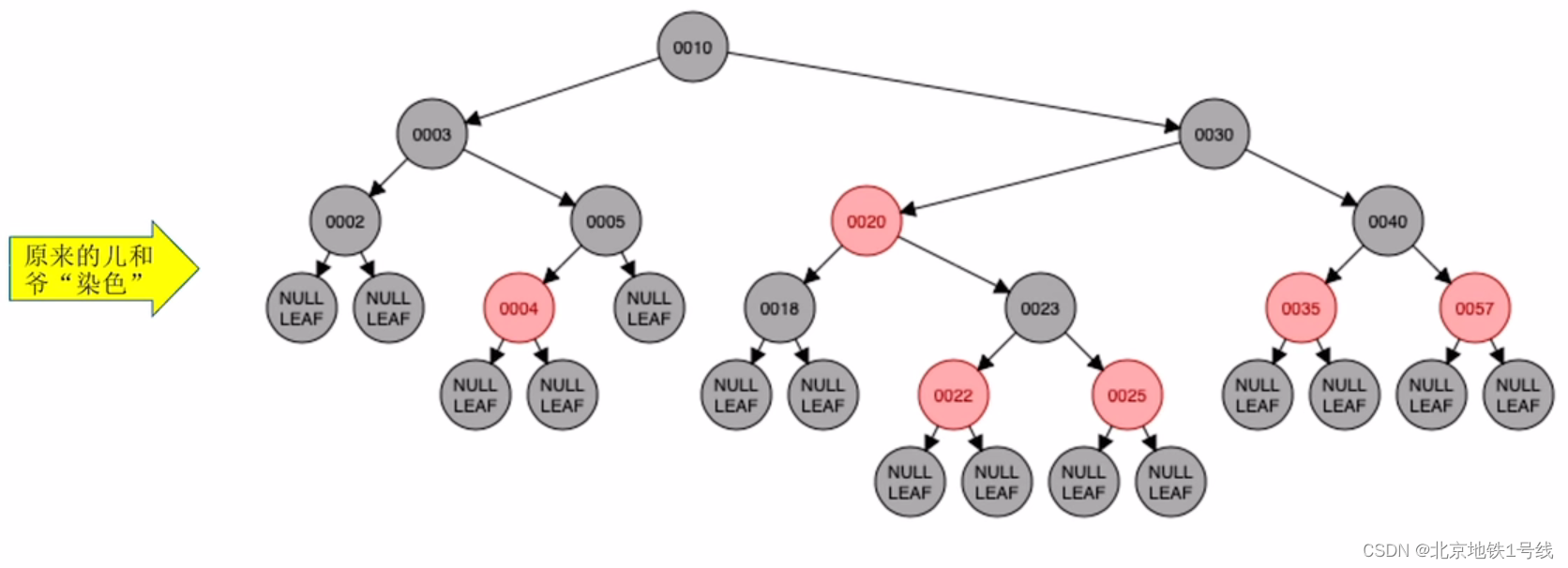
(14)插入23:此时22和23都是红结点,不满足要求4,23的叔叔结点是黑色,且从爷结点开始23是LR结点,因此执行“左、右双旋,儿换爷+染色”,经历两次旋转让儿子结点充当爷爷结点,然后改变儿子结点,爷爷结点的颜色。这里23换成黑色,25换成红色。


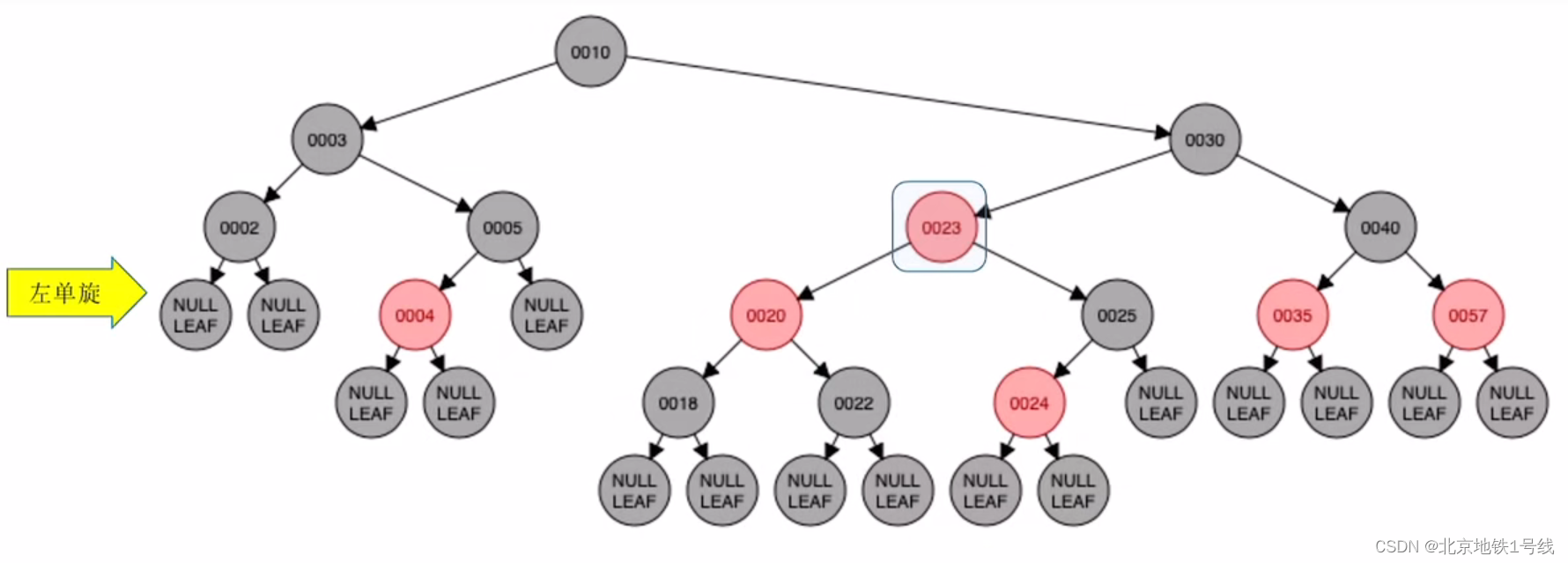
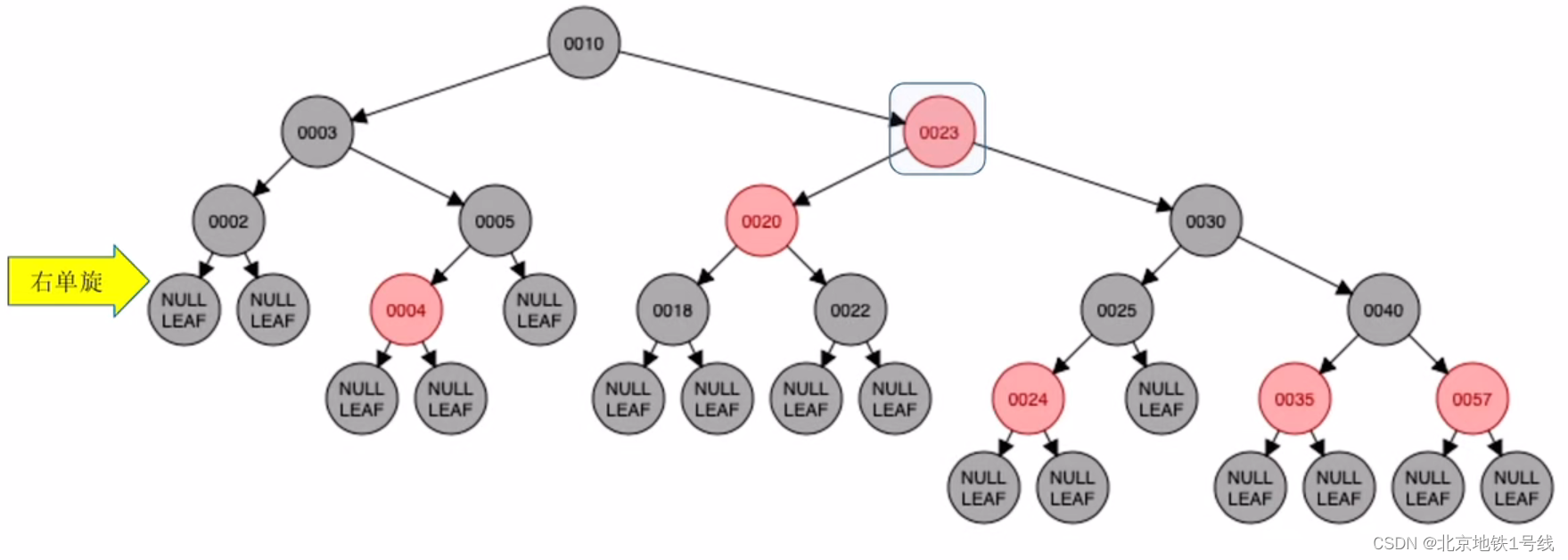

(15)插入24:此时24和25都是红结点,不满足要求4,24的叔叔结点22是红色,执行“染色+变新”,把叔叔,父亲,爷爷结点统统调换颜色,然后把爷爷结点23视为新插入的结点,再递归的执行一遍规则。23的叔叔40是黑色,且23处于LR的位置,因此执行“左、右双旋,儿换爷+染色”,经历两次旋转让儿子结点充当爷爷结点,然后改变儿子结点,爷爷结点的颜色。这里23换成黑色,30换成红色。

(16)插入19:没有破坏红黑树的要求4,所以不做任何操作。

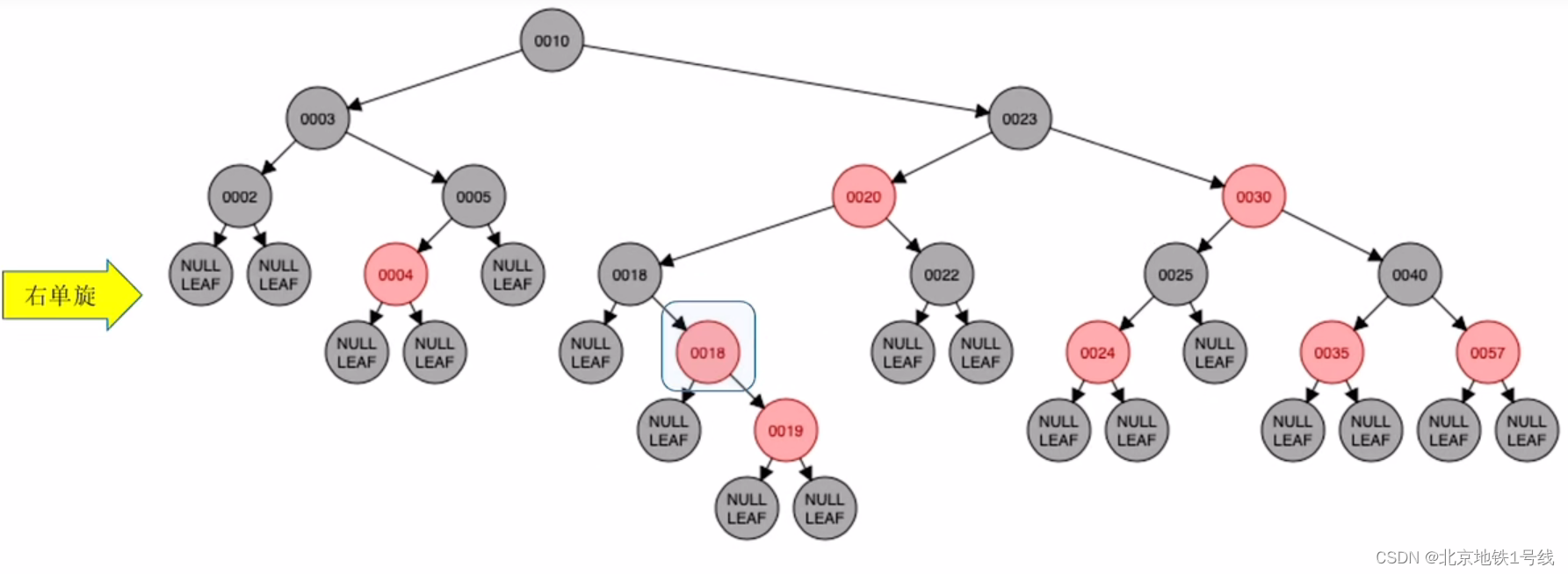


(17)插入18:这里已经有了一个18,可以直接插在黑色18的下面,也可以插在19的下面。如果插在19的下面,19的叔叔是黑色,且18处于RL的位置,因此执行“右、左双旋,儿换爷+染色”,经历两次旋转让儿子结点充当爷爷结点,然后改变儿子结点,爷爷结点的颜色。这里18换成黑色,另一个18换成红色。
四. 红黑树的删除(略)
①红黑树删除操作的时间复杂度
②在红黑树中删除结点的处理方式和二叉排序树的删除一样
③按②删除结点后,可能破坏“红黑树特性”,此时需要调整结点颜色、位置,使其再次满足“红黑树特性”。


![nginx创建站点“nginx: [emerg] host not found in upstream”错误](https://img-blog.csdnimg.cn/571a75df9780478e8fff6c815e0580ab.png#pic_center)