一、knn的缺陷
1. K-NN方法的工作机制
K-Nearest Neighbors (K-NN) 是一种基于实例的分类方法。它通过逐一比较新样本与已有样本的相似度,挑选出与新样本最接近的k个已有样本,然后根据这些样本的类别,通过投票或加权的方式来决定新样本的类别。此外,K-NN也可以应用于回归预测。在已有样本数量充足的情况下,K-NN能够取得良好的效果。研究表明,K-NN的泛化错误率不会超过贝叶斯错误率(理论最优错误率)的两倍。
2. K-NN方法的特征空间和相似度度量
K-NN方法通常使用特征空间中两个样本之间的距离(如欧氏距离、曼哈顿距离、内积等)来度量它们的相似度。这实际上假设了训练样本中每一维特征的重要性是相同的。然而,在许多情况下,样本的每一维特征对分类(或回归)问题的影响并不相同,且各维特征的数值尺度也可能不一致。因此,在应用K-NN方法时,首先需要找到合适的相似度度量方式。这需要根据实际问题进行具体的特征分析处理。
3. K-NN方法的计算复杂度和优化
虽然K-NN方法没有显式的学习过程,但在确定新样本的类别时,需要计算新样本与每一个已知样本的距离并找出前k个近邻,这在高维度的大数据集上的计算复杂度非常高。为了提高检索效率,研究人员设计了各种快速逼近最近邻(ANN)算法,如kd-tree、flann、annoy、FAISS、MRPT、KGraph、hnswlib等。在相同搜索速度(每秒查询次数,Queries/second)下的召回率(Recall)来衡量,HNSW具有最优异的性能。
4. HNSW算法的特性和应用
HNSW(Hierarchical Navigable Small World,分层可导航小世界)是一种基于图的ANN算法。HNSW利用了小世界网络的特性,即从局部看同类节点的连接呈现出规则性,从全局看不同类节点的连接呈现出随机性,来实现图的高效搜索。HNSW的编程非常简洁,特别是在mutex、lock的应用方面非常熟练,具有很高的并行性能,可以作为并行开发的参考范例。当然,程序中也存在一些可以优化的地方,如对priority_queue的应用、data_level0_ memory结构中的label的使用等。
二、基本概念
在深入探讨NSW和HNSW之前,我们需要先理解小世界网络和随机图的基本概念,这将有助于我们理解为何NSW能有效进行近邻搜索。
1. 规则图与随机图
在图论中,规则图的定义是:所有顶点的度数相同的图被称为规则图。如果每个顶点的度数都是k,那么这个图就被称为k-规则图。
而随机图则是在随机过程中生成的图,也就是说,节点之间的连接是随机建立的。
规则图与随机图的比较
在规则图中,当聚类系数接近饱和时,聚类系数较高,平均路径也较短,但此时节点的度数较高。
相比之下,随机图的节点聚类系数较低,节点的度数也较低。
2. 小世界网络
在了解了随机图和规则图之后,我们来看一下小世界网络。
1967年,Stanley Milgram从Kansas和Nebraska两个州招募了一批志愿者,他们的任务是将一封信转寄给一个住在Cambridge神学院的学生的妻子和一个住在Boston郊区的股票经纪人。
他给志愿者们设定了这样的规则:
虽然他们知道收信人的一些信息,但除非他们与收信人有私人关系,否则不能直接将信寄给收信人。
每次只能将信寄给最有可能认识收信人的熟人。
在信封中,有15张追踪卡片,每次转寄都需要将一张卡片寄回给实验者,其余的卡片则放在信封中寄给下一个人。这样,研究员就能随时追踪信件的传递路径。
在成功送达的信件中,Stanley Milgram计算出信件平均需要经过5个节点才能送达,也就是说,我们与一个陌生人建立联系只需要6步。
基于这个实验,Stanley Milgram提出了著名的“六度分离”理论。这个理论指出:
现实世界中的短路径是普遍存在的。
人们可以有效地找到并利用这些短路径。
在小世界网络中,节点之间的关系可以分为两种:
同质性:相似的节点会聚集在一起,形成邻接边。
弱连接:每个节点都会有一些随机的边连接到网络中的其他节点,这些节点是随机均匀分布的。
3. 三者的关系
有研究表明,小世界网络介于规则图和随机图之间,随着随机性的增加,规则图会呈现出小世界的特性。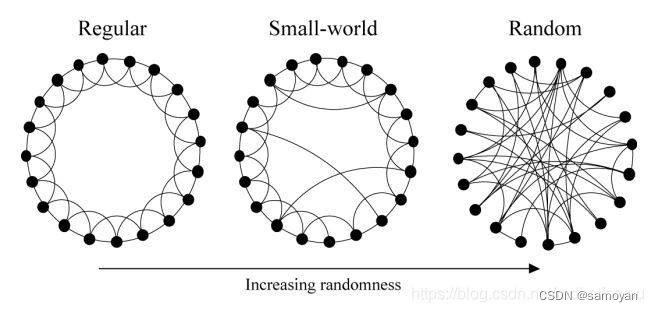
我们可以这样理解:在小世界网络中,局部的同类节点连接呈现出规则性,而从全局来看,不同类节点的连接呈现出随机性。这两种特性正是我们之前提到的同质性和弱连接。
可导航小世界网络的基本原理如下图所示:
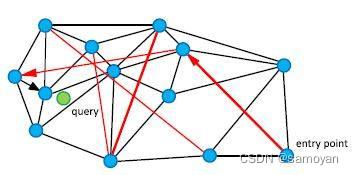
在NSW算法中,我们构建一个小世界网络,通过黑色的近邻边来寻找最近邻节点,通过红色的长边(类似于高速公路)来实现不同类节点之间的快速检索。
1. 图的搜索
在理解了NSW的基本思路后,我们来看一下在NSW中如何查找整个图中的K个最近邻节点。
K近邻搜索
在NSW中,K近邻搜索的过程如下:
随机选择一个元素,将其放入candidates集合中。
从candidates集合中选取最近邻节点c,将这些元素的邻居节点放入q集合中。
从candidates集合中移除最近邻节点c。
如果c的距离远大于result集合中的第k个节点,跳出循环。
否则,对于c的每个邻居节点,遍历其邻居,如果没有在visited set里面。
将e加入到visited set, candidates, tempRes。
遍历完成candidate中所有的节点后,将tempRes的结果传入到result。
重复执行上述步骤m遍, 返回result中最优的k个近邻结果。
2. 图的构建
根据NSW的原理,我们希望NSW的局部节点之间的距离具有同质性(即近邻节点能够相互连接)。这样当我们检索到一个近邻节点时,其大部分近邻节点都是近邻节点。同时,我们也希望保留一些随机边,以便在不同区域之间快速跳转。
那么,我们如何构建一个既具有同质性又具有随机性的小世界网络呢?
Delaunay 三角剖分 技术分享:Delaunay三角剖分算法介绍 - 知乎
为了使相邻的点在空间距离上相近,我们引入Delaunay三角剖分,相关的定义如下
Delaunay 边
在点集 V中存在两点 a 和 b,圈内不包含点集 V中的任何其他点。这个特质被称为空圈特质。
节点 a 和节点 b连接起来的边称为Delaunay边。
Delaunay 三角剖分
如果一个点集 V 的三角剖分 T 都只包含 Delaunay边,那么该三角剖分称为Delaunay剖分。
NSW节点的插入
在构建图的过程中,理论上我们应该对所有的点进行Delaunay三角剖分,然后添加一些随机的长边以构建快速检索通道,从而构建一个可导航的小世界网络。
但由于构建Delaunay三角剖分的复杂度过高,实际的代码实现过程中我们通过节点随机插入来引入随机性,利用已有节点构建Delaunay边来引入同质性。
NSW的网络构建过程如下:
在候选节点V里面随机挑选一个节点vi
将节点vi插入到已经构建好的图中,并构建边。
边构建的规则:找到节点vi最近邻的 f个邻居,建立vi和这些邻居的边连接。
在构建NSW图结构的时候,在局部通过寻找 f个最近邻来建立类似于Delaunay三角剖分的结构,
在全局通过随机顺序插入,引入随机边从而使得所以具备可导航小世界的特性。

3. 分层可导航小世界模型
在可导航小世界模型(NSW)中,图的构建阶段通过随机插入节点来引入随机性,形成一个类似小世界的网络结构。然而,NSW中存在一些显著的问题。
3.1 NSW模型的问题
- 对于最早插入的节点,其连接的邻居节点通常较远,表现出较强的弱连接属性。
- 对于最后插入的节点,其连接的邻居节点通常较近,表现出较弱的弱连接属性。
- 对于具有聚类效应的节点,由于后续插入的节点可能都与其建立连接,因此该节点的度可能较高。
这些问题引发了一个疑问:如何在继承NSW基于长链接进行快速检索,短链接具有聚类特性的思想的同时,使查找更稳定,或者如何有效区分长链接和短链接的查找。为此,引入了分层图的概念。
3.2 分层可导航小世界模型(HNSW)

HNSW是在NSW的基础上进行优化的结果,其引入了层级的概念,总体思想如下:
- 在Layer = 0层中,包含了连通图中所有的节点。
- 随着层数的增加,每一层的节点数逐渐减少并且遵循指数衰减定律。
- 图节点的最大层数,由随机指数概率衰减函数决定。
- 从某个点所在的最高层往下的所有层中均存在该节点。
- 在对HNSW进行查询的时候,从最高层开始检索。
3.3 HNSW的查询
HNSW的查询阶段包括以下几个算法:
- SEACHER-LAYER: 在指定层查询K个最近邻节点。
- SELECT-NEIGHBORS-SIMPLE: 简单的查找某一层最近的邻居节点。
- SELECT-NEIGHBORS-HEURISTIC: 探索式查找某一层最近的邻居节点。
- K-NN-SEARCH: 从所有候选结果中找出K个最近邻结果。
HNSW通过一个随机函数,将所有的点划分到不同层次,越往上节点数越少,边越少。这种情况下节点和节点之间寻找最近邻居的距离也就越远。因此在从上到下检索的过程中,先通过长链接找到全局可能的最近节点,然后往下层以该节点为入口进一步做局部检索。
4. 总结
本文主要介绍了NSW和HNSW的算法原理。NSW算法基于六度分离理论将小世界的特性用于近邻检索,提出了基于图结构的检索方案。在NSW的基础上,HNSW利用多层的图结构来完成图的构建和检索,使得通过将节点随机划分到不同的层,从上层图到下层图的检索中,越往下层节点之间的距离越近, 随机性也越差,聚类系数越高。HNSW通过从上到下的检索,完成了NSW中长链接高速公路快速检索的作用,通过最后底层的近邻检索,完成局部最近邻的查找。