1. S激活函数(sigmoid&Tanh)

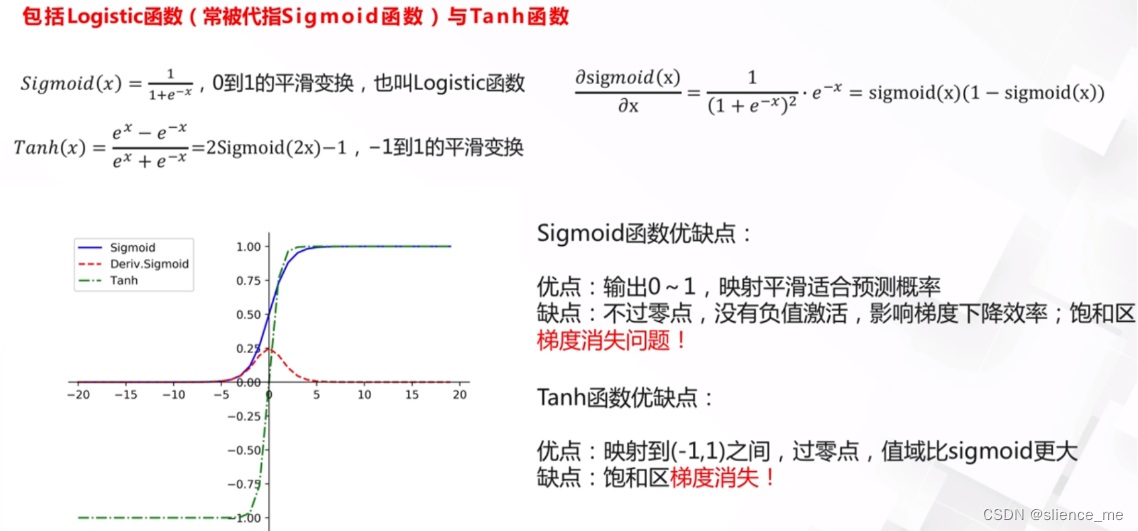
• Sigmoid函数在机器学习中经常用作激活函数，但它在某些情况下容易出现梯度消失问题，这是因为它的特性导致了梯度在饱和区域非常接近于零。

• Sigmoid函数的数学表达式如下： S(x) = 1 / (1 + e^(-x))

• 当输入x接近正无穷大（x → +∞）时，Sigmoid函数的输出趋近于1，而当输入x接近负无穷大（x → -∞）时，输出趋近于0。这意味着Sigmoid函数具有饱和性质，即在这些极端值附近，它的梯度接近于零。这就是梯度消失问题的根本原因。

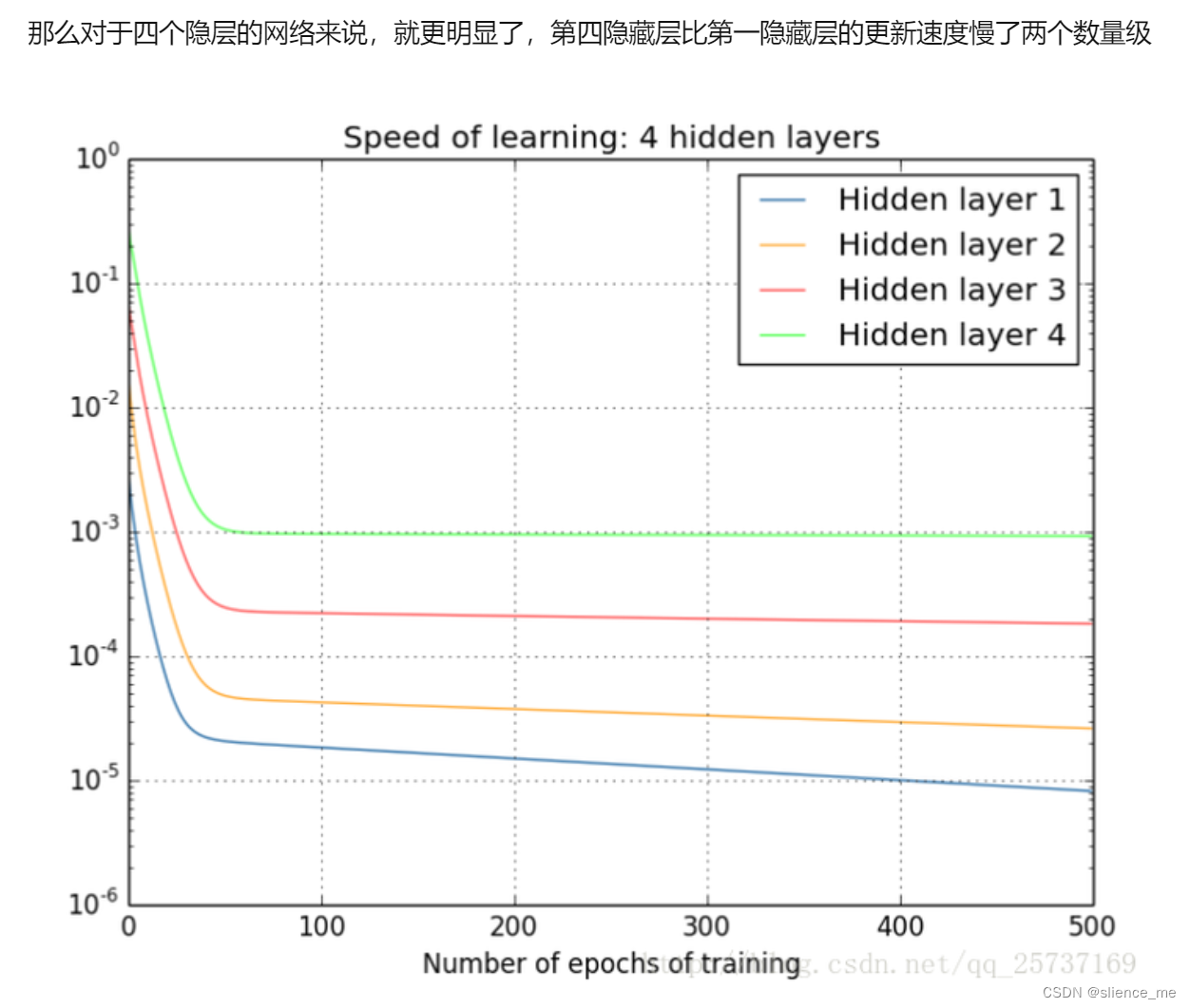
• 当你使用Sigmoid激活函数时，如果输入数据的绝对值非常大，梯度接近于零，这会导致反向传播算法中的梯度变得非常小，从而权重更新几乎不会发生，导致训练变得非常缓慢或根本无法进行有效的学习。这尤其在深度神经网络中更加明显，因为梯度会以指数方式递减，这就是为什么Sigmoid函数在深度神经网络中容易出现梯度消失问题。

• 为了克服这个问题，人们开始使用其他激活函数，如ReLU（Rectified Linear Unit）和其变种，它们不具有Sigmoid函数的饱和性质，因此在训练深度神经网络时更加稳定。ReLU激活函数的导数在正区域始终为1，因此梯度不会在正区域消失。这有助于更有效地进行梯度传播和权重更新，减少了梯度消失问题。

• Tanh（双曲正切）函数在某些情况下也可能出现梯度消失问题，尽管它相对于Sigmoid函数有一些改进，但仍然具有饱和性质，导致梯度在饱和区域接近于零。
• Tanh函数的数学表达式如下： Tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))

• Tanh函数的输出范围在-1到1之间，当输入x接近正无穷大时，它的输出趋近于1，当输入x接近负无穷大时，它的输出趋近于-1。这就意味着Tanh函数在极端值附近也具有饱和性质，梯度接近于零。

• 梯度消失问题发生的原因在于反向传播算法中的链式法则，其中导数相乘。当使用Tanh函数时，如果在网络的前向传播过程中输出值位于饱和区域，梯度将变得非常小，反向传播中的梯度也会随之减小。这会导致权重更新非常缓慢，尤其是在深度神经网络中。

• 虽然Tanh函数相对于Sigmoid函数在某些情况下更好，因为它的输出范围在-1到1之间，但在解决梯度消失问题方面，它仍然不如一些其他激活函数，如ReLU（Rectified Linear Unit）及其变种。ReLU在正区域具有恒定梯度，因此不容易出现梯度消失问题。为了克服梯度消失问题，深度神经网络中的一种常见做法是使用ReLU或其变种，同时采用一些正则化技术和初始化策略来稳定训练过程。

2. ReLU激活函数

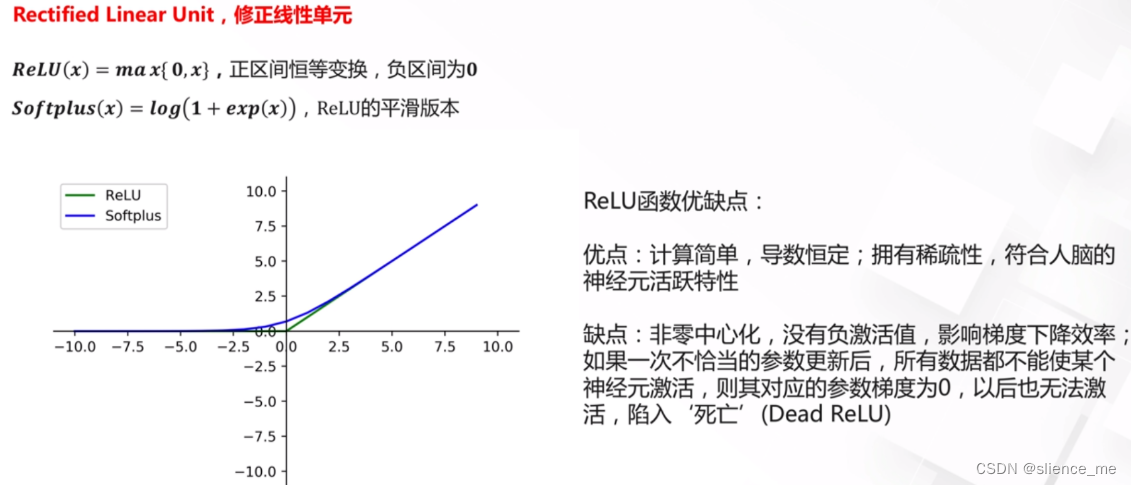
• ReLU（Rectified Linear Unit）是一种常用的激活函数，它在输入大于零时输出输入值，而在输入小于或等于零时输出零。这意味着ReLU是非零中心化的，因为它的输出的均值（平均值）不是零，而是正的。这与一些其他激活函数，如tanh和Sigmoid不同，它们的输出均值通常接近于零。
• 为什么ReLU是非零中心化的并且没有负激活值，可以归结为其定义方式。ReLU函数的数学表达式如下： f(x) = max(0, x)

• 在这个函数中，当输入x大于零时，它输出x，而当输入x小于等于零时，输出零。这意味着ReLU在正区域（x>0）内有激活值，但在负区域（x<=0）内没有激活值。因为ReLU截断了负值，所以其均值是正的。

• 这种非零中心化的性质有一些影响：
  1. 梯度消失问题缓解：与tanh和Sigmoid等激活函数不同，ReLU在正区域的梯度始终为1，这有助于减轻梯度消失问题，因为梯度不会在正区域消失。
  2. 稀疏激活性：由于ReLU在负区域没有激活值，神经元可以学习选择性地激活，这有助于网络的稀疏表示，这意味着每个神经元仅在特定情况下激活，而其他时候保持静止，这对于特征选择和表示学习很有用。

• 尽管ReLU有许多优点，但它也有一些问题，例如死亡神经元问题，其中某些神经元在训练中永远保持非活跃状态。为了克服这些问题，人们发展了一些ReLU的变种，如Leaky ReLU和Parametric ReLU（PReLU），它们允许小的负输入值通过，从而改善了ReLU的性能。这些变种可以使神经网络更容易训练。

3. ReLU激活函数的改进

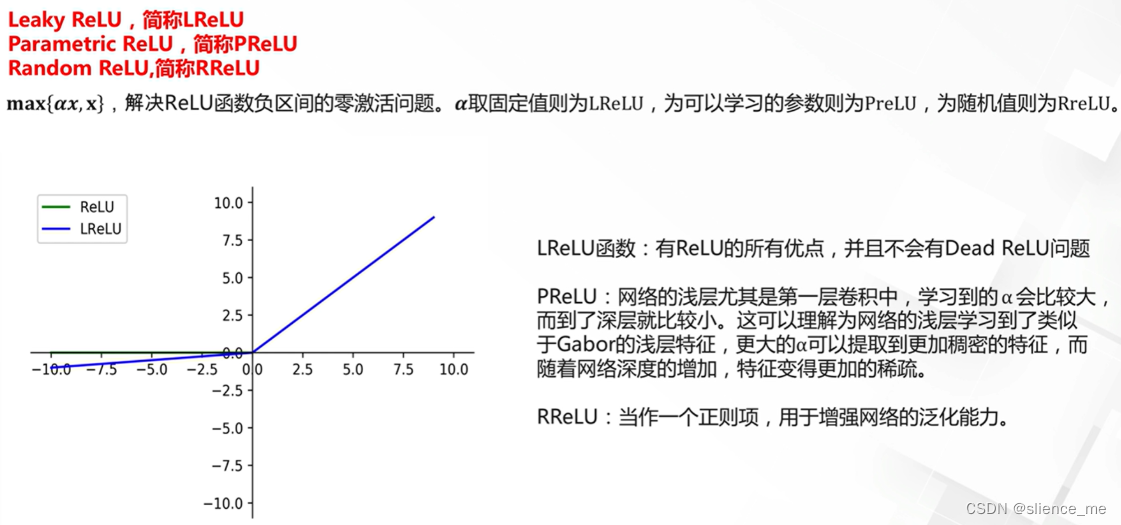
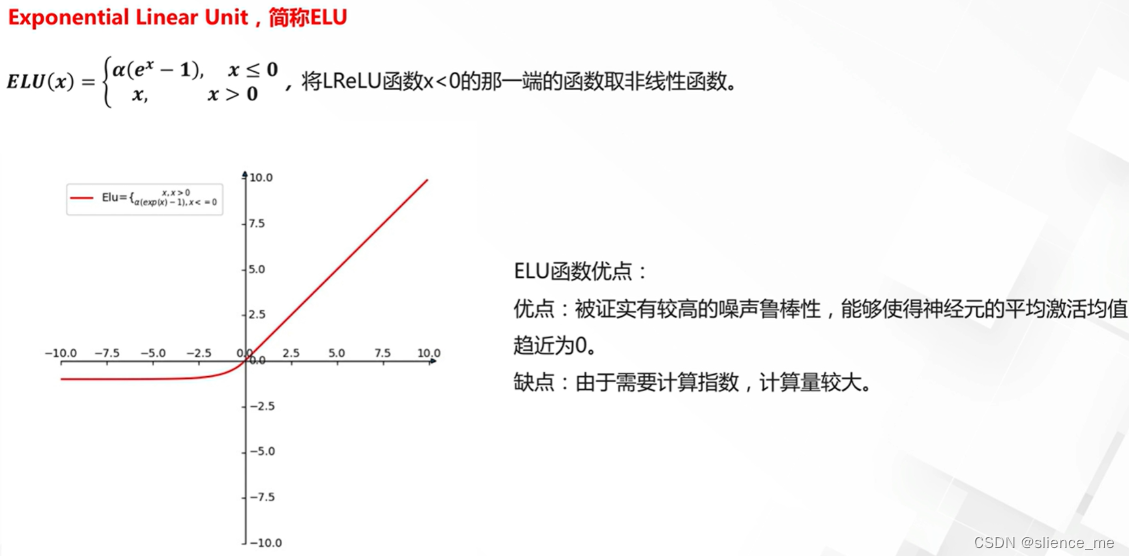
4. 近似ReLU激活函数

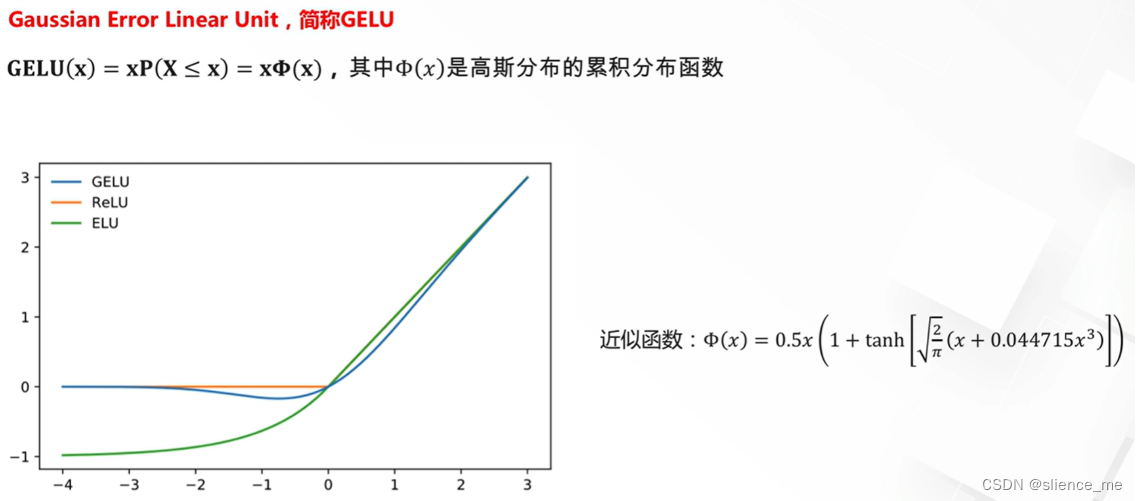
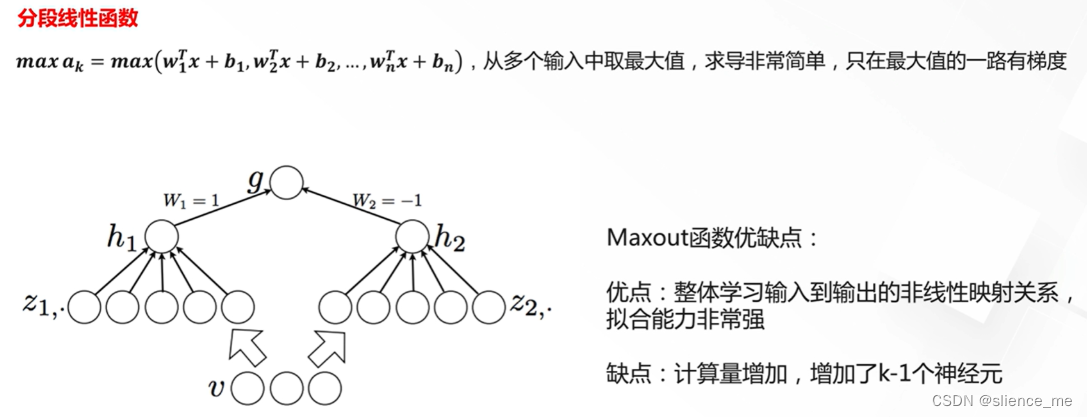
5. Maxout激活函数

• Maxout是一种激活函数，它在深度学习中用于神经网络的非线性变换。与传统的激活函数如ReLU、Sigmoid和tanh不同，Maxout具有独特的结构，它的主要特点是取输入的最大值，因此可以视为线性片段的极大化。以下是Maxout激活函数的定义：
• 对于Maxout激活函数，给定多个线性组合的输入，它将这些线性组合中的最大值作为输出。具体来说，考虑两个线性组合：
  Z1 = w1x + b1
  Z2 = w2x + b2
• Maxout激活函数输出的值为：Maxout(x) = max(Z1, Z2)

• Maxout的主要特点和优点包括：
  1. 非线性性质：Maxout函数是一种非线性激活函数，因为它取输入中的最大值，从而引入了非线性性质，使神经网络能够学习更复杂的函数。
  2. 灵活性：Maxout允许神经网络学习不同的线性片段，而不受限于单一的线性关系。这可以增加模型的表达能力，有助于处理各种数据分布和特征。
  3. 抗噪声性：Maxout激活函数在一定程度上对噪声具有抗性，因为它取输入中的最大值，可以消除一些不必要的噪声信号。
  4. 降低过拟合风险：Maxout具有更多的参数，允许网络在训练中拟合更多的数据，从而降低了过拟合的风险。

• 尽管Maxout在理论上具有一些优势，但在实际应用中，它并不像ReLU那样常见。这是因为Maxout的参数数量较多，可能需要更多的数据和计算资源来训练。此外，ReLU和其变种在实践中通常表现得非常出色，因此它们更常见。然而，Maxout仍然是一个有趣的激活函数，特别适用于特定的深度学习任务和研究领域。

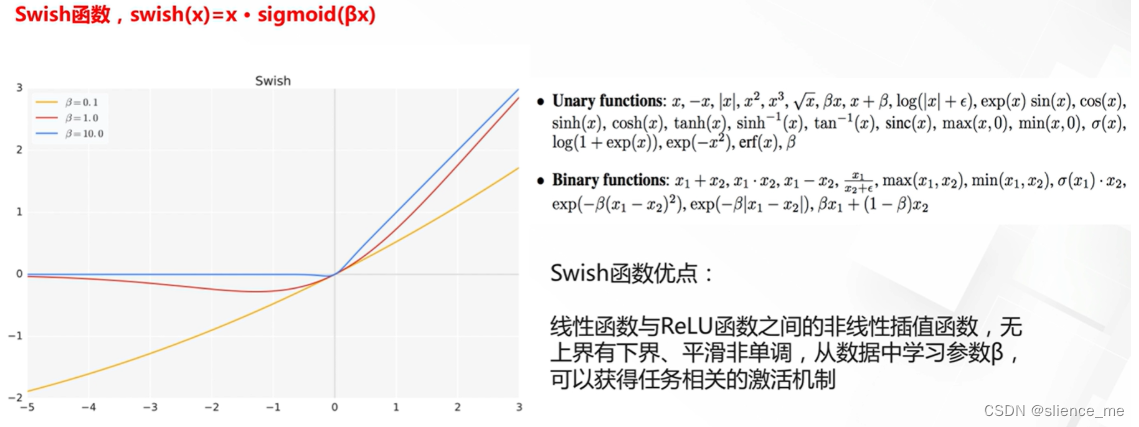
6. 自动搜索的激活函数Swish

• Swish是一种激活函数，最初由Google研究员在2017年提出。Swish函数的定义如下：Swish(x) = x * sigmoid(x)
• 其中，x是输入，sigmoid(x)表示x经过S型函数（Sigmoid函数）的输出。Swish函数是一种非线性激活函数，它在一定程度上结合了线性和非线性的特性。

• Swish函数的特点和优势包括：
  1. 平滑性：Swish函数是平滑的，与ReLU等分段线性函数相比，它在激活值的变化上更加平滑。这有助于梯度的更加连续传播，有助于训练深度神经网络。
  2. 非线性性质：Swish在Sigmoid函数的基础上引入了非线性，这使得它能够捕捉更复杂的数据模式，使神经网络更具表达能力。
  3. 渐进性：与ReLU不同，Swish函数在输入趋于正无穷大时不会饱和，而是渐进地接近于线性函数x。这意味着Swish函数在正值区域仍然具有一定的非线性性质，从而有助于避免一些梯度消失问题。
  4. 可学习性：Swish函数是可学习的，它的参数（例如，Sigmoid函数的斜率）可以通过反向传播算法进行调整，以适应特定任务和数据分布。

• 尽管Swish在理论上有一些优势，但在实践中，它的性能通常介于ReLU和Sigmoid之间。因此，选择使用Swish还是其他激活函数取决于具体的任务和实验。有时，Swish可能对某些问题效果很好，但对于其他问题，标准的ReLU或其变种仍然是首选。在深度学习中，激活函数通常是可以调整的超参数，因此可以进行实验来选择最适合特定任务的激活函数。

注意：部分内容来自 阿里云天池