输出n阶螺旋矩阵中指定位置的元素值

---

问题描述：

---

问题分析：

经观察，易知螺旋矩阵由内层至外层依次递减，为以 $n^2$为首项，以-1为公差的等差数列 。分奇数阶和偶数阶矩阵分类讨论，分别归纳得$n^2$所在的行和列的通项公式。 故考虑从最大值位置开始依次向目标位置移动，统计出总共移动步数(step),目标位置的值= $n^2-step$ ；

1)当$n$为奇数时：$n^2$所在的行和列分别为$(n+1)/2,(n+1)/2;$
2）当$n$为偶数时，$n^2$所在的行和列分别为$n/2+1,n/2$

由于螺旋矩阵由内往外螺距逆时针旋转逐渐递增，在矩阵中的任意一个位置上有且只有“上、下、左、右”四个方向选择如图：

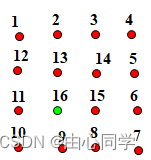
偶数阶时，将右、上归为一组，左、下 归为一组；
奇数阶时，将左、下归为一组，右、上归为一组；
以组为单位进行移动，每组移动过后，step++,······直到到达目标位置为止，并计算出该位置的元素值即可。

---

C++实现：

#include<iostream>
int Solve(int n,int i, int j) {
    /*
    查找螺旋矩阵中指定位置的元素的值
    算法描述：
        分奇数阶和偶数阶矩阵分类讨论，分别归纳得出n*n所在的行和列的通项公式。
        由于螺旋矩阵内层到外层依次递减，
        故考虑从最大值位置开始依次向目标位置移动，统计出总共移动步数(step),目标位置的值= n*n-step ；
    
    */
    int step = 0;
    int move = 1;
    if (n % 2 != 0) {
        //输出n*n所在的行和列
        int x = (n + 1) / 2;
        int y = (n + 1) / 2;
        //std::cout << "x=" << x << " ," << "y=" << y << std::endl;
        if (x == i && y == j) { return n * n; }
        while (true) {
            //left
            y -=move;
            step += move;            
            if (x == i && y <= j && j<=y+move) { step -= (j - y); return n * n - step; }
            //down
            x += move;
            step += move;
            if (x >=i &&i>=x-move && y == j) { step -= (x - i); return n * n - step; }
            move++;
            //right
            y += move;
            step += move;
            if (x == i && y >= j && j>=y-move) { step -= ( y-j); return n * n - step; }
            //up
            x -= move;
            step += move;
            if (x <= i &&i<=x+move && y ==j) { step -= (i-x); return n * n - step; }
            move++;
            if (x == 1 && y == n) { move--; }
        }
        std::cout << "x=" << x << " ," << "y=" << y << std::endl;
    }

    int x = n / 2 + 1;
    int y = n / 2;
    
    if (x == i && y == j) { return n * n; }
    while (true) {
        //right
        y += move;
        step += move;
        if (x == i && y >= j && j>=y-move) { step -= (y - j); return n * n - step; }
        //up
        x -= move;
        step += move;
        if (x <= i && i<=x+move && y == j) { step -= (i - x); return n * n - step; }
        move++;
        //left
        y -= move;
        step += move;
        if (x == i && y <= j && j<=y+move) { step -= (j - y); return n * n - step; }
        //down
        x += move;
        step += move;
        if (x >= i && i>=x-move && y == j) { step -= (x - i); return n * n - step; }
        move++;
        if (x == 1 && y == n) { move--; }
        std::cout << "x=" << x << " ," << "y=" << y << std::endl;
    }
        
}

int main() {
    int i = 0, j= 0,n=0;
    std::cout << "Please enter  n、i、j:" << std::endl;
    //while (true) {
        std::cin >> n >> i >> j;
        std::cout << Solve(n, i, j) << std::endl;
    //}
    system("pause");
    return 0;
}

文末，或词不达意，欢迎大家评论交流 !