给定一个数组，和一个正整数$k$，将数组重复$k$次
找到最大子数组和

如果$k=1$，那就和以前的最大子数组和是一样的

接着又几种可能
考虑原数组和为$sum$

如果$sum>0$,那么有可能最大为$sum\ast k$
也可能是还是原来数组的最大子数组和

最重要的是要考虑如果这个最大子数组可以夸数组

因此我们可以先求两个数组的最大子数组和
如果$sum>0$，那么答案为$two\_max+(k-2)\ast sum$

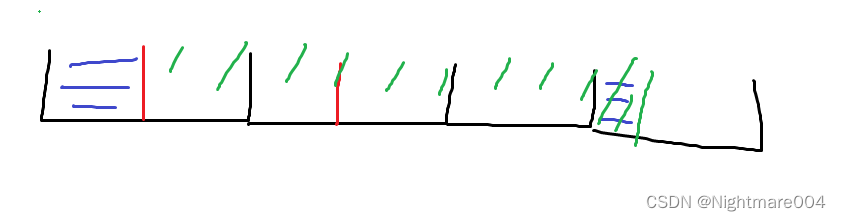
图中红色为两个数组的最大子数组和，绿色是答案

class Solution {
public:
    const int MOD = 1e9 + 7;
    int kConcatenationMaxSum(vector<int>& arr, int k) {
        int n = arr.size(), cur = arr[0], mx = arr[0], sum = accumulate(arr.begin(), arr.end(), 0);
        for(int i = 1; i < n * min(k, 2); ++i){
            cur = max(cur + arr[i % n], arr[i % n]);
            mx = max(cur, mx);
        }
        return max(0LL, mx + 1LL * max(0, k - 2) * max(sum, 0)) % MOD;
    }
};