leetcode 1372 二叉树中的最长交错路径
给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下:
- 选择二叉树中 任意 节点和一个方向(左或者右)。
- 如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。
- 改变前进方向:左变右或者右变左。
- 重复第二步和第三步,直到你在树中无法继续移动。
交错路径的长度定义为:访问过的节点数目 - 1(单个节点的路径长度为 0 )。
请你返回给定树中最长 交错路径 的长度。
示例 1:
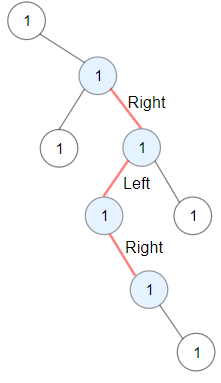
输入:root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1] 输出:3 解释:蓝色节点为树中最长交错路径(右 -> 左 -> 右)。示例 2:
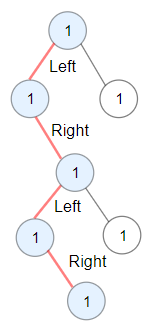
输入:root = [1,1,1,null,1,null,null,1,1,null,1] 输出:4 解释:蓝色节点为树中最长交错路径(左 -> 右 -> 左 -> 右)。示例 3:
输入:root = [1] 输出:0
常规的深搜题
如果该结点是双亲的左子树,那遍历该结点左子树的时候从0计数,遍历该结点右子树的时候沿用上一层的ZigZag值;反之。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def longestZigZag(self, root):
"""
:type root: TreeNode
:rtype: int
"""
def nextLevel(root, lastDirection, maxZigZag):
maxZigZag += 1
leftZigZag = rightZigZag = maxZigZag
if lastDirection == 'L':
if root.right:
rightZigZag = nextLevel(root.right, 'R', maxZigZag)
if root.left:
leftZigZag = nextLevel(root.left, 'L', 0)
return max(leftZigZag, rightZigZag)
if lastDirection == 'R':
if root.left:
leftZigZag = nextLevel(root.left, 'L', maxZigZag)
if root.right:
rightZigZag = nextLevel(root.right, 'R', 0)
return max(leftZigZag, rightZigZag)
if not root.left and not root.right:
return 0
maxZigZag = 0
leftZigZag = rightZigZag = maxZigZag
if root.left:
leftZigZag = nextLevel(root.left, 'L', maxZigZag)
if root.right:
rightZigZag = nextLevel(root.right, 'R', maxZigZag)
return max(leftZigZag, rightZigZag)
leetcode 236 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。 因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1
感觉把自己绕晕了...写了半天没写出来,直接看题解了:
如果一个结点是p和q的公共祖先,p与q的分布则满足三种情况:
- p与q一个在左子树中,一个在右子树中
- p就是公共祖先,q在其左或右子树中
- q就是公共祖先,p在其左或右子树中
通过递归对二叉树进行先序遍历,当遇到节点 p 或 q 时返回。从底至顶回溯,当节点 p,q 在节点 root的异侧时,节点 root即为最近公共祖先,则向上返回 root
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root in (None, p, q):
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left and right:
return root
return left or right