课上

归并排序 

最大时，就是两个都是完全倒序，但注意一定有一个序列先用完，此时剩一个序列只有一个元素，不用比较，直接加入，所以就是n+n-1,

最小时，是都是完全有序，且一个序列中的元素完全，全部小于另一个序列中元素，但每次都需要第一个值进行比较，直到小的序列全用完，就直接一直不用比较加剩下的序列中元素

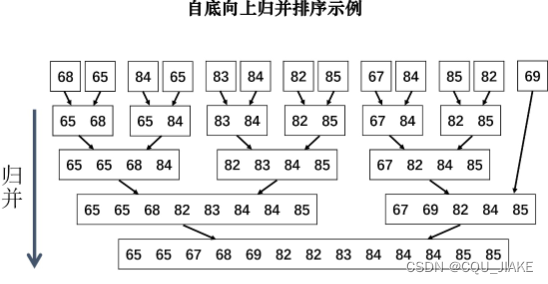
自顶向下

 自底向上

这个意思是说，确定外层确定子序列的长度，然后每次都从这个序列的头部开始，逐渐合并外层确定长度的子序列，即内层循环为不断归并两个长度相同（为外层确定的长度）的子序列，直到左子序列的左端到达当前序列的尾部

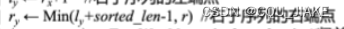这句需注意

确定左子序列左端，然后根据当前子序列长度，确定右子序列左端，左子序列右端，由于内层判断是lx<=r-len,所以左子序列右端，右子序列左端一定可以直接加减得到，但是右子序列右端不能确定，所以需要一个min函数

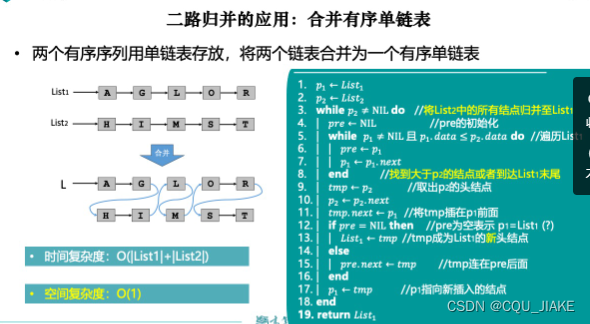
链表合并

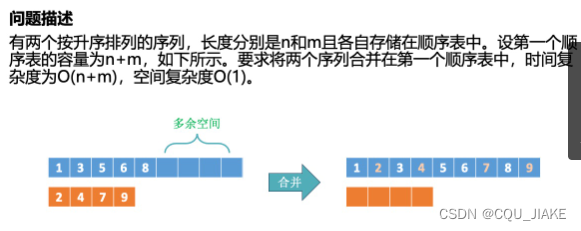
经典面试题

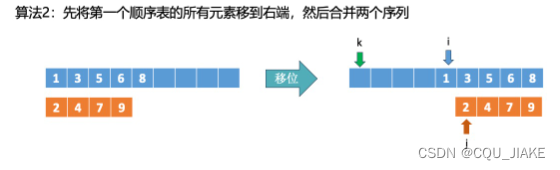
极端情况是一直动二号顺序表的元素，那就说明二号顺序表元素都比一号顺序小，那么k到i时，一号顺序表都在对应正确的位置

其他情况下，移动一号顺序表，就意味着一号顺序表长度变短了

另一种极端情况是一直移动一号顺序表，那么k到j时，二号顺序表都在正确位置

如果不倒置，就是在原基础上按大的排，即之前倒置是比较两个表头哪个小，把小的放前面，现在是比较表尾哪个大，把大的放后面，就可以直接在原来基础上排序

逆序对

就是后面的序列表头元素放到前面时，就相当于此时这个元素比前面的所有元素都小，都能构成逆序对，即逆序对数量+前面序列剩余的长度

如果前面的表头元素移动，和后面的不构成逆序对，其内部也在底层递归时统计过，所以就没有逆序对产生，即只在后面序列前移时产生逆序对

翻转对（力扣493）

逆序对依然产生在后面序列中，只不过需要再加一个条件判断 

回顾

 冒泡排序

每次都可以选出一个当前最大值，那么后续比较的时候尾部长度逐渐减小，

每次比较都要从第一个元素开始

void bubbleSort(vector<int>& v){//冒泡排序
    for(int i = 0; i < v.size(); i++){
        for(int j = 0; j < v.size() - i - 1; j++){
            if(v[j] > v[j + 1])
                swap(v[j], v[j + 1]);
        }
    }
}

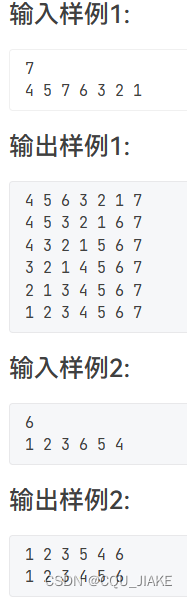
说让排序完成时

快速排序最快nlogn,最差n^2