搜素二叉树
- 二叉搜索树的使用
- 二叉搜索树的模拟实现(K)
- 整体结构
- 循环版本
- 递归版本
- 二叉搜索树的应用
- 源码(kv)
二叉搜索树的使用
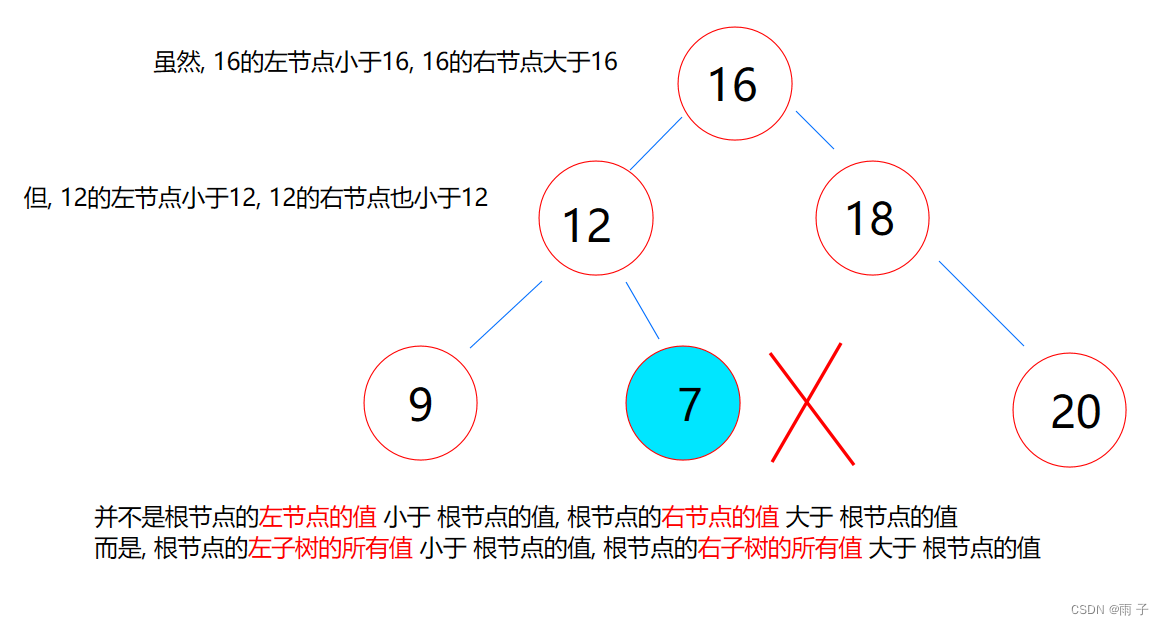
二叉搜索树 相较于 普通的二叉树来说:
- 根节点的左子树的所有键值都
小于根节点, 根节点的右子树的所有键值大于根节点 - 根节点的
左右子树 都是 二叉搜索树 中序遍历是升序的⇒ 二叉搜素树 又叫作二叉排序树
- 子树 && 节点
- 查找
假如查找 key, 有如下四种情况:- 如果 key
>根节点的值, 那么就去根节点的右子树去查找 - 如果 key
<根节点的值, 那么就去根节点的左子树去查找 - 如果 key
=根节点的值, 那么就找到了 - 如果找到
空, 那就不存在
- 如果 key
- 查找的时间复杂度是
O(高度次), 而不是O(logN)
如果是完全二叉树, 那么就是O(logN);如果退化到极限情况, 类似于链表, 那么就是O(N)

所以, 总结下来, 时间复杂度就是O(高度次)
那么如何解决这种退化问题呢? ⇒AVL树 和 红黑树 就是针对这种情况做了特殊处理 --> 旋转
-
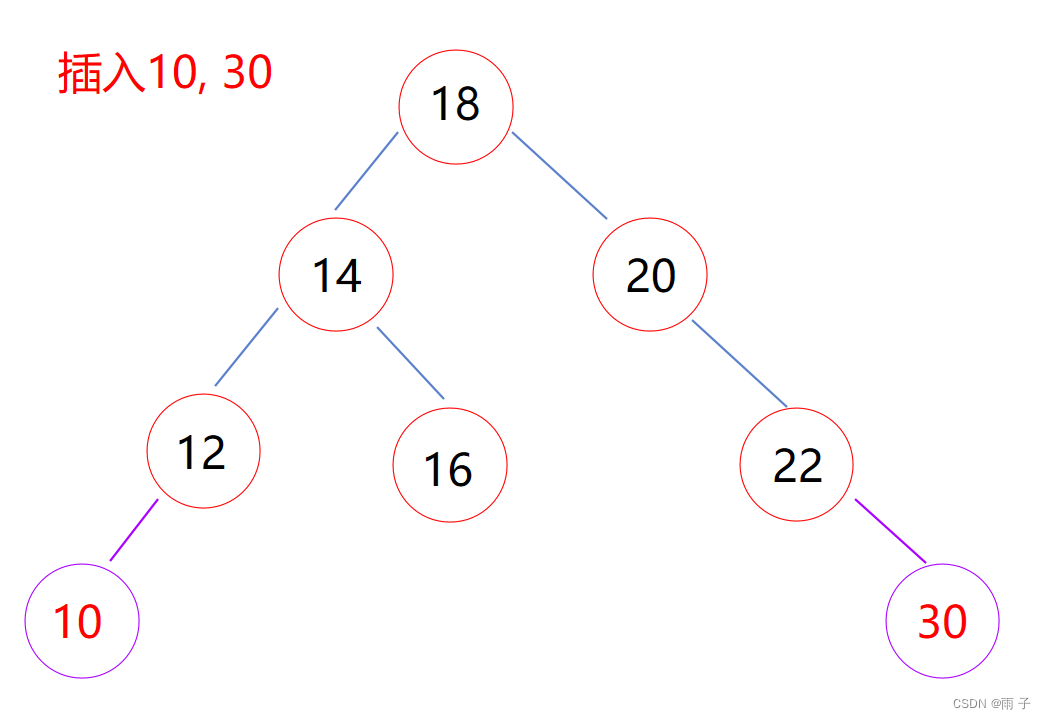
插入
总体思想:找到非空节点去插入
-
删除key
- 先找到key的位置, 有两种情况:
- 没找到, 那就直接返回
- 找到了key的位置, 记作cur. 找到了也有三种情况:
- cur的左子树为空
- cur的右子树为空
- cur的左右子树都不为空
- 先找到key的位置, 有两种情况:
由于 cur要进行删除, 要把cur后面的内容链接到parent的后面. && cur也有两种可能 parent的左子树 or 右子树 ⇒ 我们要cur后面的内容链接到 cur处于parent的位置
删除具体如下👇👇👇
- cur的右子树为空
(1) cur是parent的左子树
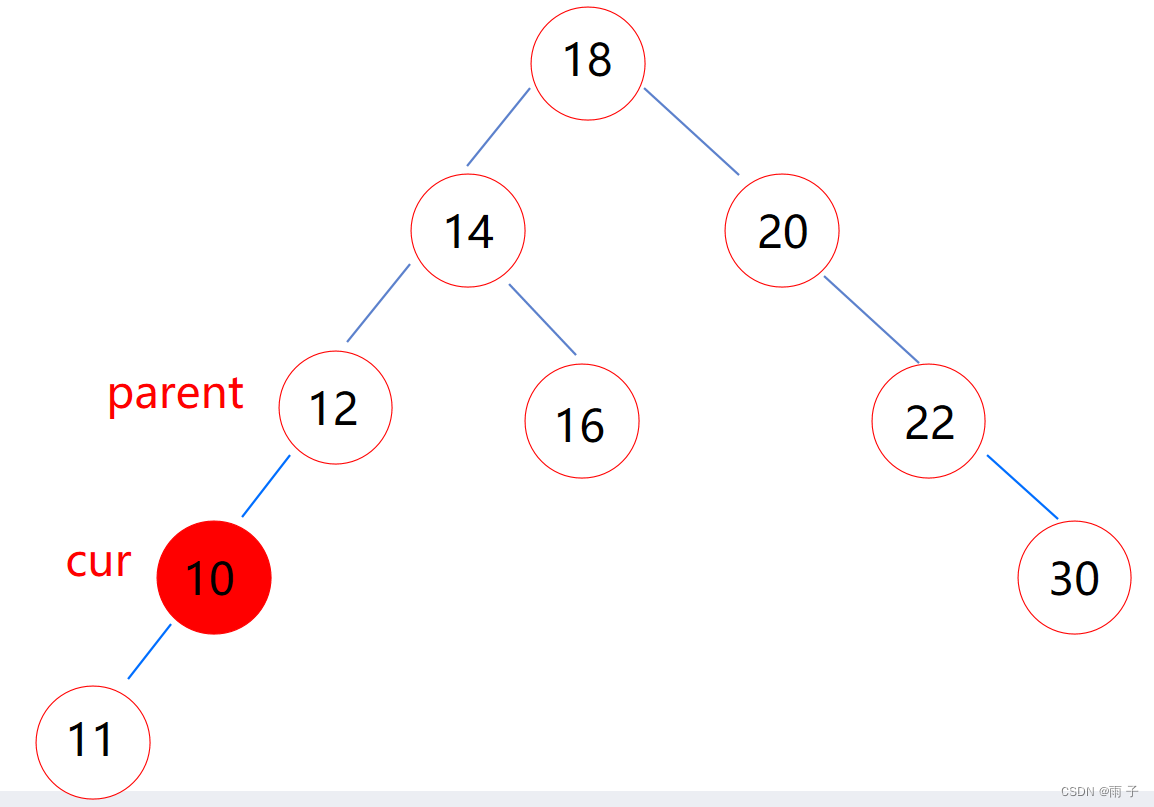
(2) cur是parent的右子树
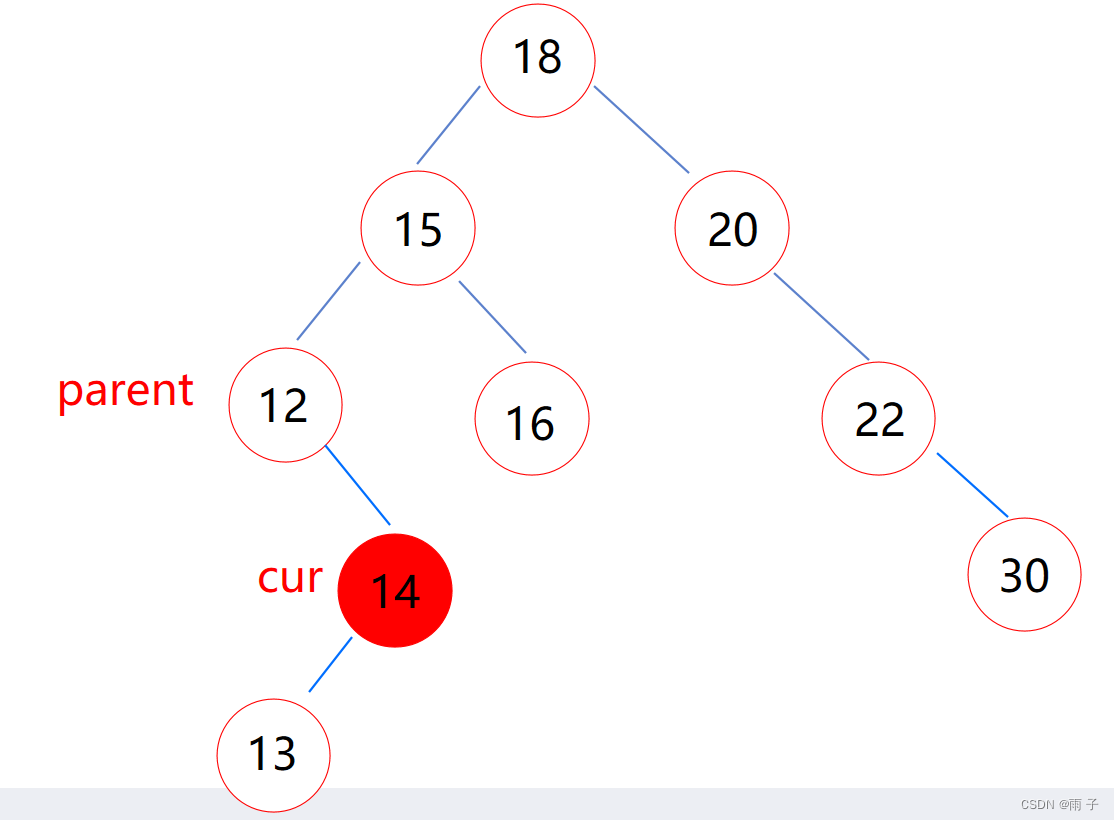
- cur的左子树为空
(1) cur是parent的左子树
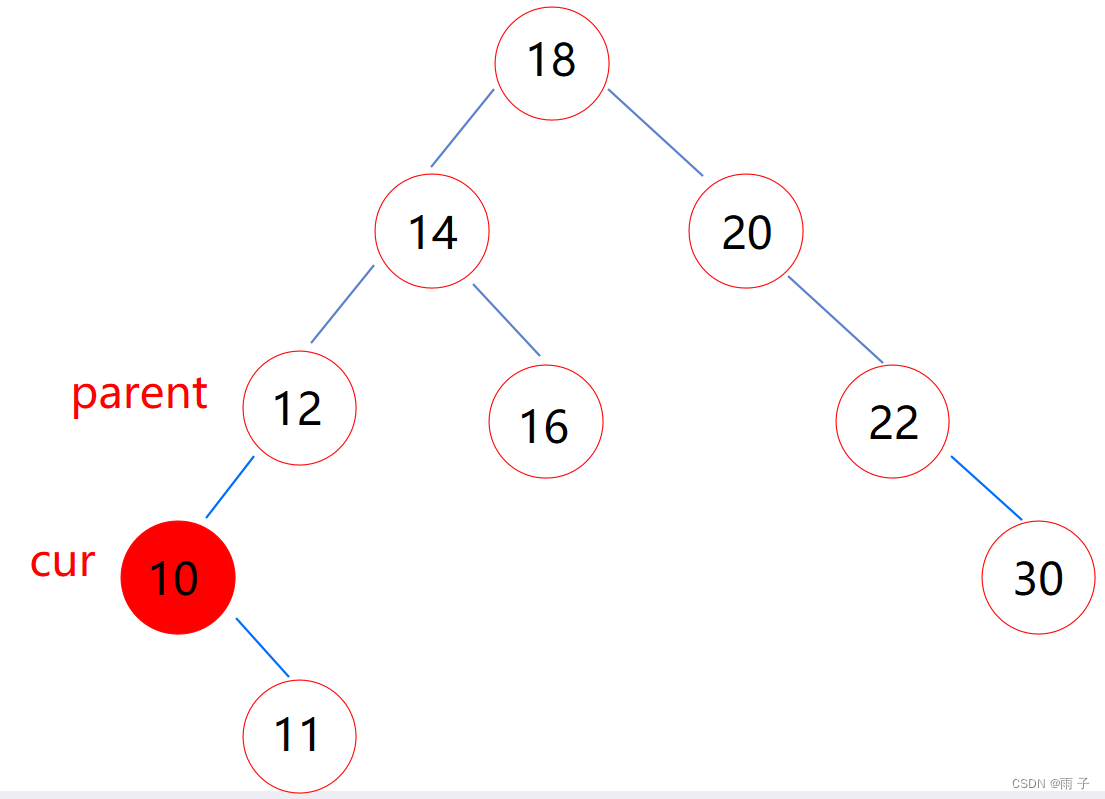
(2) cur是parent的右子树

- cur的左右子树都不为空
🗨️删除掉cur, 那么我们如何链接cur的左右子树呢?-
可以找一个节点来替换掉cur, 然后我们来处理这个节点的链接关系就好了
🗨️替换过去, 也不改变二叉搜索树的结构, 那么节点是什么好呢? 后面集中处理这个节点, 那么这个节点应该容易处理才对, 那么这个节点是叶子节点吗? - 替换过去, 不改变二叉树的结构 — —
替换节点应该为 cur的左子树的最大节点 或者 cur的右子树的最小节点⇐中序遍历, cur旁边的两个数; 中序是 左跟右, ⇒ 那么就应该是左子树的最大节点, 或者右子树的最小节点
左子树的最大节点, 或者右子树的最小节点; 正好是叶子节点⇒ 那么我们处理这个替换节点也比较容易⇒ 思想同上替换节点的左子树为空, 或 替换节点的右子树为空
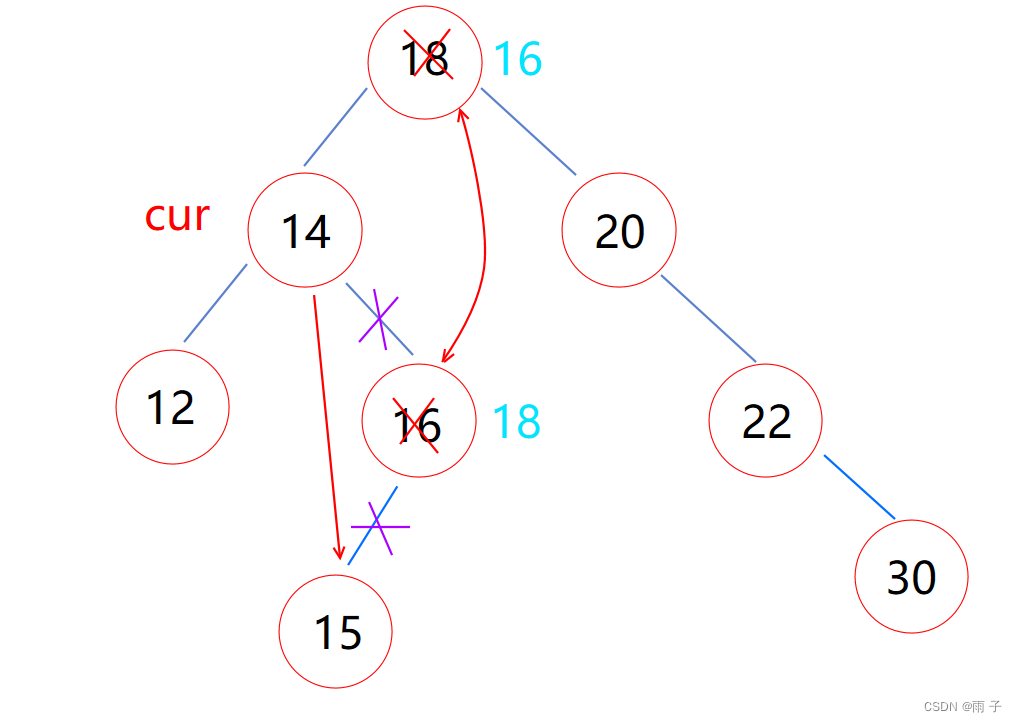
-
二叉搜索树的模拟实现(K)
整体结构
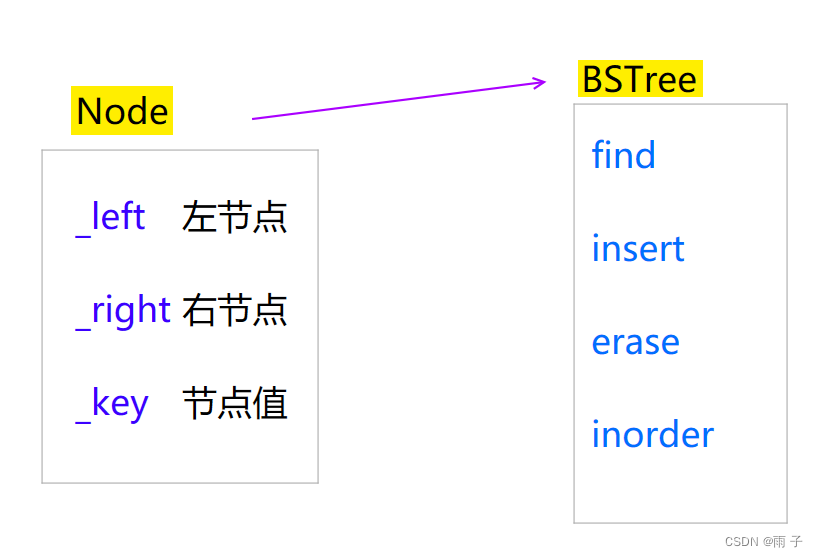
Node类
template<class T>
struct BSTreeNode
{
public:
BSTreeNode(const T& key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
public:
BSTreeNode<T>* _left;
BSTreeNode<T>* _right;
T _key;
};
BSTree类
template<class T>
class BSTree
{
typedef BSTreeNode<T> Node;
public:
BSTree()
:_root(nullptr)
{}
// 析构函数
~BSTree()
{
_BSTree(_root);
}
private:
// 析构函数
void _BSTree(Node* root)
{
if (root == nullptr)
return;
// 后序遍历进行删除
_BSTree(root->_left);
_BSTree(root->_right);
delete root;
}
// 成员函数
Node* _root;
}
循环版本
- find
Node* find(const K& key)
{
return _find(_root, key);
}
private:
Node* _find(Node* root, const T& key)
{
Node* cur = root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
- insert
bool insert(const T& key)
{
Node* newnode = new Node(key);
if (_root == nullptr)
{
_root = newnode;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
// 寻找插入的位置
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
break;
}
}
// 链接
if (key > parent->_key)
{
parent->_right = newnode;
}
else if (key < parent->_key)
{
parent->_left = newnode;
}
else
{
return false;
}
return true;
}
- inorder
void Inorder()
{
_Inorder(_root);
}
private:
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
std::cout << root->_key << " ";
_Inorder(root->_right);
}
- erase

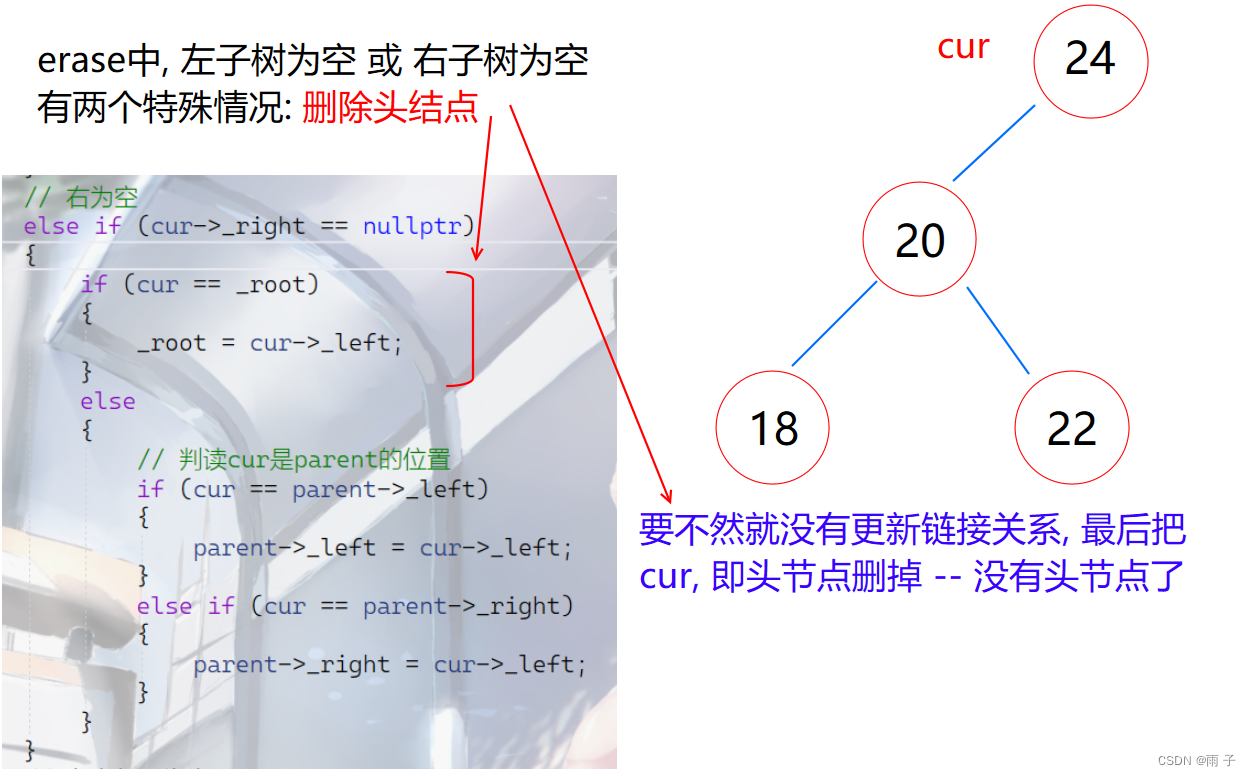
bool erase(const T& key)
{
return _erase(_root, key);
}
private:
bool _erase(Node* root, const T& key)
{
// 先找到位置
Node* parent = root;
Node* cur = root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
// 找到了
else
{
// 左为空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
// 判读cur是parent的位置
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else if (cur == parent->_right)
{
parent->_right = cur->_right;
}
}
}
// 右为空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
// 判读cur是parent的位置
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else if (cur == parent->_right)
{
parent->_right = cur->_left;
}
}
}
// 左右都不为空
else
{
// 先找到cur的左子树的最大值 或 右子树的最小值
// parent必须初始化为cur -- 以防删除的就是头节点
Node* parent = cur;
Node* LeftMax = cur->_left;
while (LeftMax->_right)
{
parent = LeftMax;
LeftMax = LeftMax->_right;
}
// 交换cur 和 LeftMax的值
std::swap(cur->_key, LeftMax->_key);
// 改变链接关系
if (parent->_left == LeftMax)
{
parent->_left = LeftMax->_left;
}
else if (parent->_right == LeftMax)
{
parent->_right = LeftMax->_left;
}
cur = LeftMax;
}
// 集中释放 cur
delete cur;
return true;
}
}
return false;
}
递归版本
- findr
无需链接关系— —不用引用即可- 递归退出条件
root == nullptr, 那就返回nullptr - 根据二叉搜索数的特性: 大了往右边走, 小了往左边走, 相等就返回当前节点的指针;
- 递归退出条件
Node* findr(const T& key)
{
return _findr(_root, key);
}
private:
Node*_findr(Node* root, const T& key)
{
if (root == nullptr)
return nullptr;
if (key < root->_key)
{
_findr(root->_left, key);
}
else if (key > root->_key)
{
_findr(root->_right, key);
}
else
{
return root;
}
}
- insertr
需要重新链接 -- -- 引用的妙用
总体思想 :遇到空就插入- 递归返回条件 :
遇到空, 插入后, 返回true - 二叉树的特性: 大了往右边走, 小了往左边走, 相等返回false
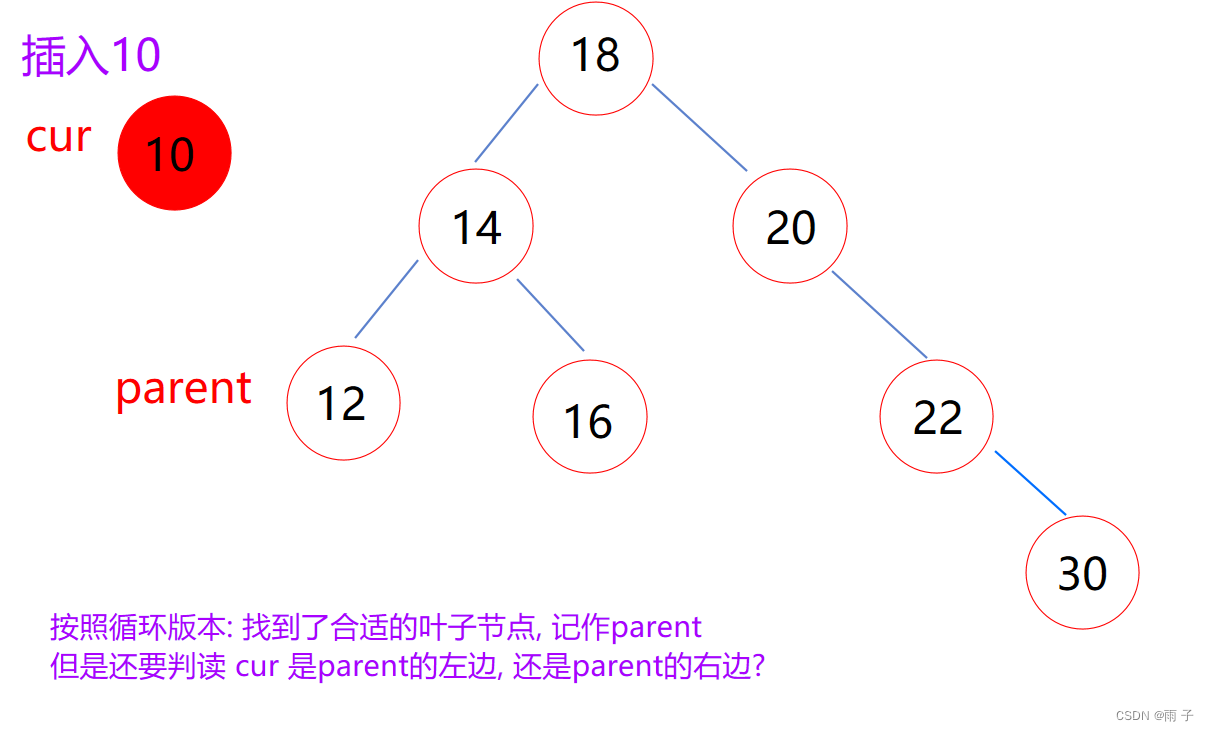
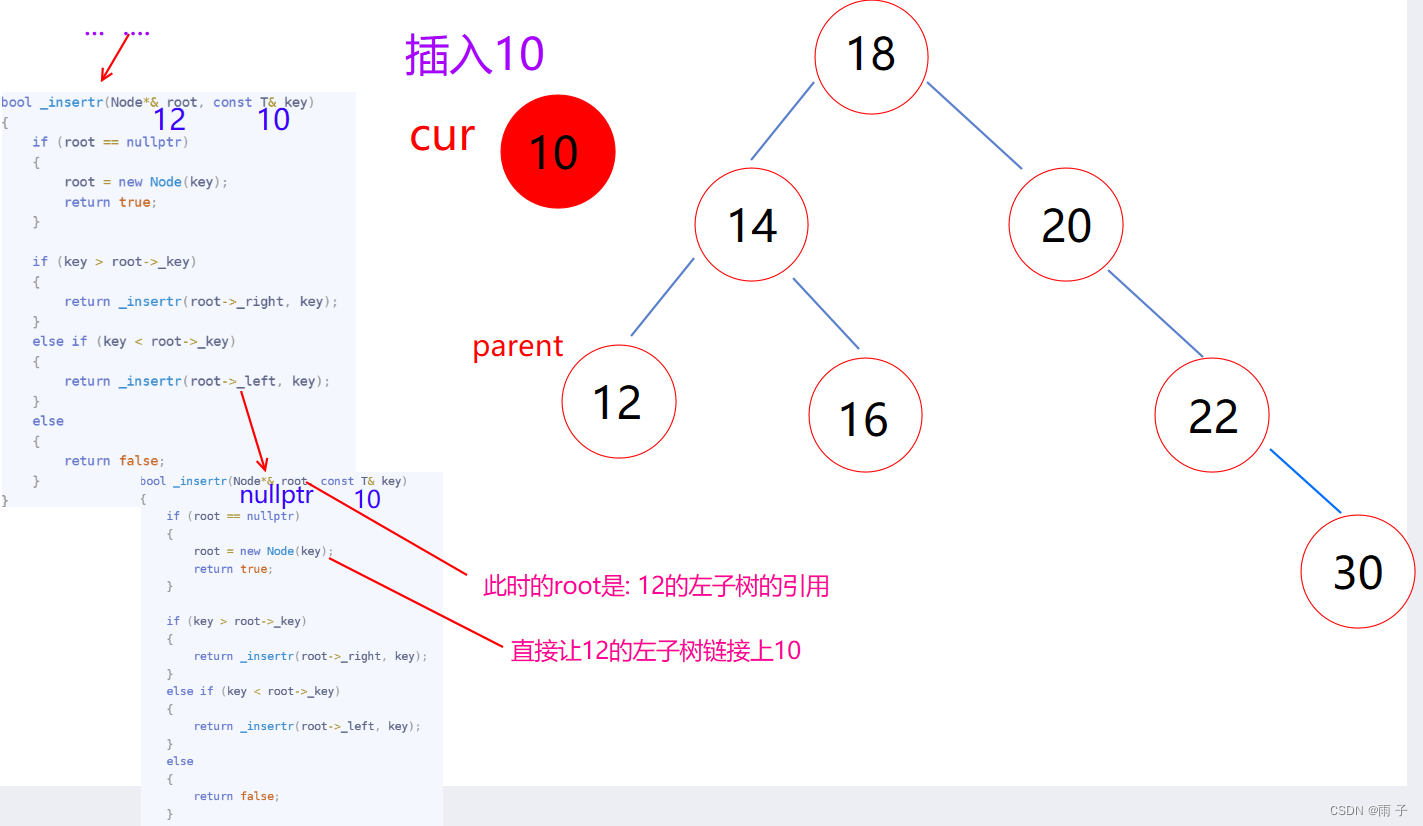
- 递归返回条件 :
bool insertr(const T& key)
{
return _insertr(_root, key);
}
private:
bool _insertr(Node*& root, const T& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (key > root->_key)
{
return _insertr(root->_right, key);
}
else if (key < root->_key)
{
return _insertr(root->_left, key);
}
else
{
return false;
}
}
- eraser
需要重新链接 -- -- 引用的妙用- 递归结束条件: 遇到空就返回 false
- 先找到位置, 记作 cur
- cur有三种情况 :
cur的左子树为空, cur的右子树为空, cur的左右子树都不为空; 三种情况分类讨论
这个和上面的 引用的妙用是一样的道理, 那么我就不在这里画 递归展开图
bool eraser(const T& key)
{
return _eraser(_root, key);
}
private:
bool _eraser(Node*& root, const T& key)
{
if (root == nullptr)
{
return false;
}
if (key > root->_key)
{
_eraser(root->_right, key);
}
else if (key < root->_key)
{
_eraser(root->_left, key);
}
else
{
// 由于是上面节点的引用 && 要删掉root节点
// ⇒ 找一个背锅侠来代替root节点去删除
Node* tem = root;
// 左子树为空
if (root->_left == nullptr)
{
root = root->_right;
}
//右子树为空
else if (root->_right == nullptr)
{
root = root->_left;
}
// 左右子树都不为空
else
{
// 找到左树的最大节点
Node* maxleft = root->_left;
while (maxleft->_right)
{
maxleft = maxleft->_right;
}
// 交换root 和 maxleft的值
std::swap(maxleft->_key, root->_key);
// 重新链接
root = maxleft->_left;
// 背锅侠就位
tem = maxleft;
}
// 统一删除
delete tem;
return true;
}
return false;
}
二叉搜索树的应用
二叉搜索树主要有两个版本 K版本 和 KV版本
KV版本 相较于 K版本 就多了个 value
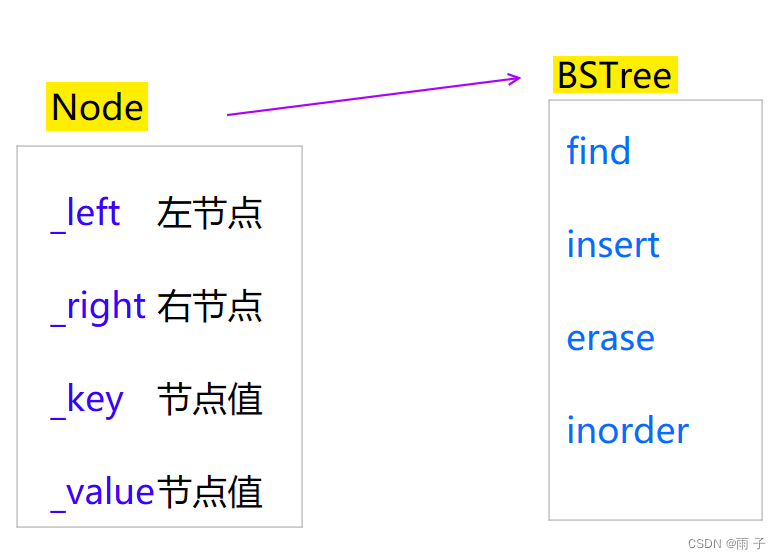
template<class K, class V>
struct BSTreeNode
{
public:
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
,_right(nullptr)
,_key(key)
,_value(value)
{}
public:
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
K _key;
V _value;
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(nullptr)
{}
private:
Node* _root;
}
由于 还是对 K 进行操作 ⇒ 我们这里就不写 KV的代码了. 后面源码会附上 KV的完整代码
二叉搜索树主要应用于两种模型: K模型 和 KV模型
- K模型 — — 根据关键码Key去解决
在不在的问题
比如 : 判断单词是否拼写错误 (将词库导入二叉搜索树, 然后判断在不在)
void test1()
{
// 模拟导入词库
muyu::BSTree<string, string> World;
World.insert("insert", "插入");
World.insert("input", "输入");
World.insert("output", "输出");
World.insert("love", "爱情");
string str;
while (cin >> str)
{
// 查找是否在词库中出现
auto ret = World.find(str);
if (ret)
{
cout << "输入正确" << endl;
}
else
{
cout << "查无单词, 请重新输入" << endl;
}
}
}
int main()
{
test1();
return 0;
}
运行结果:

- KV模型 — — 每一个关键码Key, 都有一个与之对应的 Value, 存在
<Key, Value>键值对
比如: 统计水果出现的次数
void test2()
{
muyu::BSTree<string, int> cnt;
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };
for (const auto& e : arr)
{
auto res = cnt.find(e);
// 第一次插入, 次数就给个1
if (!res)
{
cnt.insert(e, 1);
}
// 不是第一次插入, 就在key对应的value进行++
else
{
res->_value++;
}
}
cnt.Inorder();
}
int main()
{
test2();
return 0;
}
运行结果:
苹果 6
西瓜 3
香蕉 2
源码(kv)
#pragma once
namespace muyu
{
template<class K, class V>
struct BSTreeNode
{
public:
BSTreeNode(const K& key = K(), const V& value = V())
:_left(nullptr)
,_right(nullptr)
,_key(key)
,_value(value)
{}
public:
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
K _key;
V _value;
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(nullptr)
{}
~BSTree()
{
_BSTree(_root);
}
bool insert(const K& key, const V& value)
{
Node* newnode = new Node(key, value);
if (_root == nullptr)
{
_root = newnode;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
// 寻找插入的位置
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
break;
}
}
// 链接
if (key > parent->_key)
{
parent->_right = newnode;
}
else if (key < parent->_key)
{
parent->_left = newnode;
}
else
{
return false;
}
return true;
}
bool insertr(const K& key)
{
return _insertr(_root, key);
}
void Inorder()
{
_Inorder(_root);
}
Node* find(const K& key)
{
return _find(_root, key);
}
Node* findr(const K& key)
{
return _findr(_root, key);
}
bool erase(const K& key)
{
return _erase(_root, key);
}
bool eraser(const K& key)
{
return _eraser(_root, key);
}
private:
void _BSTree(Node* root)
{
if (root == nullptr)
return;
// 后序遍历进行删除
_BSTree(root->_left);
_BSTree(root->_right);
delete root;
}
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
std::cout << root->_key << " " << root->_value << std::endl;
_Inorder(root->_right);
}
Node* _insertr(Node*& root, const K& key, const V& value)
{
if (root == nullptr)
{
root = new Node(key, value);
return root;
}
if (key > root->_key)
{
return _insertr(root->_right, key);
}
else if (key < root->_key)
{
return _insertr(root->_left, key);
}
else
{
return nullptr;
}
}
Node* _find(Node* root, const K& key)
{
Node* cur = root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
Node* _findr(Node* root, const K& key)
{
if (root == nullptr)
return nullptr;
if (key < root->_key)
{
_findr(root->_left, key);
}
else if (key > root->_key)
{
_findr(root->_right, key);
}
else
{
return root;
}
}
bool _erase(Node* root, const K& key)
{
// 先找到位置
Node* parent = root;
Node* cur = root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
// 找到了
else
{
// 左为空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
// 判读cur是parent的位置
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else if (cur == parent->_right)
{
parent->_right = cur->_right;
}
}
}
// 右为空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
// 判读cur是parent的位置
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else if (cur == parent->_right)
{
parent->_right = cur->_left;
}
}
}
// 左右都不为空
else
{
// 先找到cur的左子树的最大值 或 右子树的最小值
Node* parent = cur;
Node* LeftMax = cur->_left;
while (LeftMax->_right)
{
parent = LeftMax;
LeftMax = LeftMax->_right;
}
// 交换cur 和 LeftMax的值
std::swap(cur->_key, LeftMax->_key);
// 改变链接关系
if (parent->_left == LeftMax)
{
parent->_left = LeftMax->_left;
}
else if (parent->_right == LeftMax)
{
parent->_right = LeftMax->_left;
}
cur = LeftMax;
}
delete cur;
return true;
}
}
return false;
}
bool _eraser(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (key > root->_key)
{
_eraser(root->_right, key);
}
else if (key < root->_key)
{
_eraser(root->_left, key);
}
else
{
Node* tem = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* maxleft = root->_left;
while (maxleft->_right)
{
maxleft = maxleft->_right;
}
std::swap(maxleft->_key, root->_key);
root = maxleft->_left;
tem = maxleft;
}
delete tem;
return true;
}
return false;
}
Node* _root;
};
}
晚日寒鸦一片愁。柳塘新绿却温柔。若教眼底无离恨,不信人间有白头。
肠已断,泪难收。相思重上小红楼。情知已被山遮断,频倚阑干不自由。
— — 辛弃疾· 《鹧鸪天》