前言

小编研究生的研究方向是视觉SLAM,目前在自学,本篇文章为初学高翔老师课的第二次作业。
文章目录
- 前言
- 1.熟悉 Eigen 矩阵运算
- 2.几何运算练习
- 3.旋转的表达
- 4.罗德里格斯公式的证明
- 5.四元数运算性质的验证
- 6.熟悉 C++11
1.熟悉 Eigen 矩阵运算
设线性⽅程 Ax = b,在 A 为⽅阵的前提下,请回答以下问题:
- 在什么条件下, x 有解且唯⼀?
- ⾼斯消元法的原理是什么?
- QR 分解的原理是什么?
- Cholesky 分解的原理是什么?
- 编程实现 A 为 100 × 100 随机矩阵时,⽤ QR 和 Cholesky 分解求 x 的程序。你可以参考本次课⽤到的 useEigen 例程。
1.当r(A)=r([A|b])=n时,也就是A满秩,A可逆,方程组有唯一解。
2.高斯消元法如图所示:

3.QR的分解原理如图所示:
4.Cholesky分解的原理如下图:
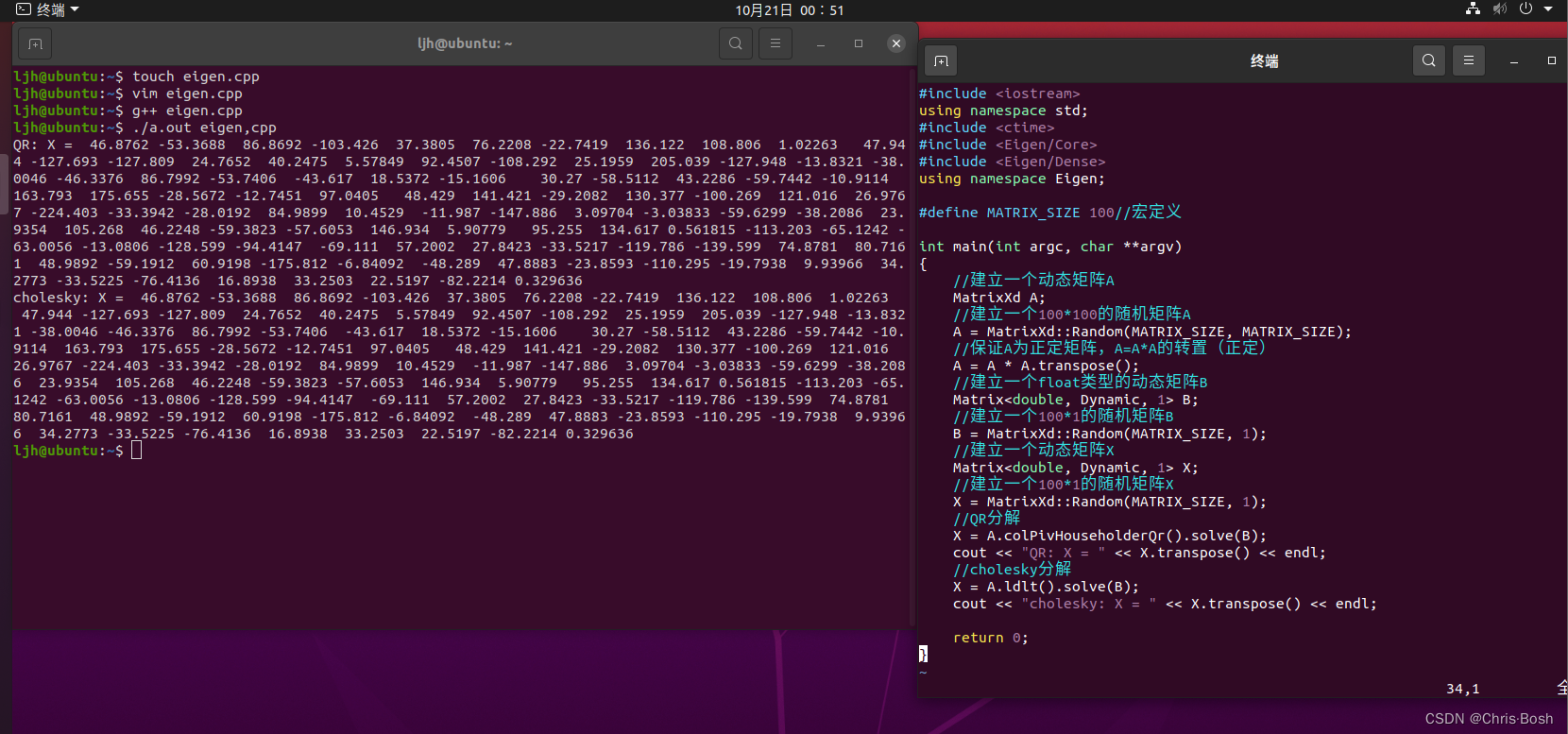
5. 编程实现 A 为 100 × 100 随机矩阵时,⽤ QR 和 Cholesky 分解求 x 的程序。你可以参考本次课⽤到的 useEigen 例程。提⽰:你可能需要参考相关的数学书籍或⽂章。请善⽤搜索引擎。 Eigen 固定⼤⼩矩阵最⼤⽀持到 50,所以你会⽤到动态⼤⼩的矩阵。
其实这题就是让我们自己建立一个AX=B,利用Eigen的内置函数求解X
代码如下:
#include <iostream>
using namespace std;
#include <ctime>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace Eigen;
#define MATRIX_SIZE 100//宏定义
int main(int argc, char **argv)
{
//建立一个动态矩阵A
MatrixXd A;
//建立一个100*100的随机矩阵A
A = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
//保证A为正定矩阵,A=A*A的转置(正定)
A = A * A.transpose();
//建立一个float类型的动态矩阵B
Matrix<double, Dynamic, 1> B;
//建立一个100*1的随机矩阵B
B = MatrixXd::Random(MATRIX_SIZE, 1);
//建立一个动态矩阵X
Matrix<double, Dynamic, 1> X;
//建立一个100*1的随机矩阵X
X = MatrixXd::Random(MATRIX_SIZE, 1);
//QR分解
X = A.colPivHouseholderQr().solve(B);
cout << "QR: X = " << X.transpose() << endl;
//cholesky分解
X = A.ldlt().solve(B);
cout << "cholesky: X = " << X.transpose() << endl;
return 0;
}
运行结果如下:
Eigen的语法规则,及其用法参考如下:
#include <iostream>
using namespace std;
#include <ctime>
// Eigen 部分
#include <Eigen/Core>
// 稠密矩阵的代数运算(逆,特征值等)
#include <Eigen/Dense>
#define MATRIX_SIZE 50
/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/
int main( int argc, char** argv )
{
// Eigen 中所有向量和矩阵都是Eigen::Matrix,它是一个模板类。它的前三个参数为:数据类型,行,列
// 声明一个2*3的float矩阵
Eigen::Matrix<float, 2, 3> matrix_23;
// 同时,Eigen 通过 typedef 提供了许多内置类型,不过底层仍是Eigen::Matrix
// 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>,即三维向量
Eigen::Vector3d v_3d;
// 这是一样的
Eigen::Matrix<float,3,1> vd_3d;
// Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>
Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero(); //初始化为零
// 如果不确定矩阵大小,可以使用动态大小的矩阵
Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;
// 更简单的
Eigen::MatrixXd matrix_x;
// 这种类型还有很多,我们不一一列举
// 下面是对Eigen阵的操作
// 输入数据(初始化)
matrix_23 << 1, 2, 3, 4, 5, 6;
// 输出
cout << matrix_23 << endl;
// 用()访问矩阵中的元素
for (int i=0; i<2; i++) {
for (int j=0; j<3; j++)
cout<<matrix_23(i,j)<<"\t";
cout<<endl;
}
// 矩阵和向量相乘(实际上仍是矩阵和矩阵)
v_3d << 3, 2, 1;
vd_3d << 4,5,6;
// 但是在Eigen里你不能混合两种不同类型的矩阵,像这样是错的
// Eigen::Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;
// 应该显式转换
Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;
cout << result << endl;
Eigen::Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;
cout << result2 << endl;
// 同样你不能搞错矩阵的维度
// 试着取消下面的注释,看看Eigen会报什么错
// Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d;
// 一些矩阵运算
// 四则运算就不演示了,直接用+-*/即可。
matrix_33 = Eigen::Matrix3d::Random(); // 随机数矩阵
cout << matrix_33 << endl << endl;
cout << matrix_33.transpose() << endl; // 转置
cout << matrix_33.sum() << endl; // 各元素和
cout << matrix_33.trace() << endl; // 迹
cout << 10*matrix_33 << endl; // 数乘
cout << matrix_33.inverse() << endl; // 逆
cout << matrix_33.determinant() << endl; // 行列式
// 特征值
// 实对称矩阵可以保证对角化成功
Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose()*matrix_33 );
cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;
// 解方程
// 我们求解 matrix_NN * x = v_Nd 这个方程
// N的大小在前边的宏里定义,它由随机数生成
// 直接求逆自然是最直接的,但是求逆运算量大
Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
Eigen::Matrix< double, MATRIX_SIZE, 1> v_Nd;
v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );
clock_t time_stt = clock(); // 计时
// 直接求逆
Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;
cout <<"time use in normal inverse is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;
// 通常用矩阵分解来求,例如QR分解,速度会快很多
time_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout <<"time use in Qr decomposition is " <<1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;
return 0;
}
2.几何运算练习
下⾯我们来练习如何使⽤ Eigen/Geometry 计算⼀个具体的例⼦。 设有⼩萝⼘ 1⼀号和⼩萝⼘⼆号位于世界坐标系中。⼩萝⼘⼀号的位姿为: q1 = [0:55; 0:3; 0:2; 0:2]; t1 =[0:7;1:1; 0:2]T(q 的第⼀项为实部)。这⾥的 q 和 t 表达的是 Tcw,也就是世界到相机的变换关系。⼩萝⼘⼆号的位姿为 q2 = [−0:1; 0:3; −0:7; 0:2]; t2 = [−0:1; 0:4;0:8]T。现在,⼩萝⼘⼀号看到某个点在⾃⾝的坐标系下,坐标为 p1 = [0:5; −0:1; 0:2]T,求该向量在⼩萝⼘⼆号坐标系下的坐标。请编程实现此事,并提交你的程序。
提⽰:
- 四元数在使⽤前需要归⼀化。
- 请注意 Eigen 在使⽤四元数时的虚部和实部顺序。
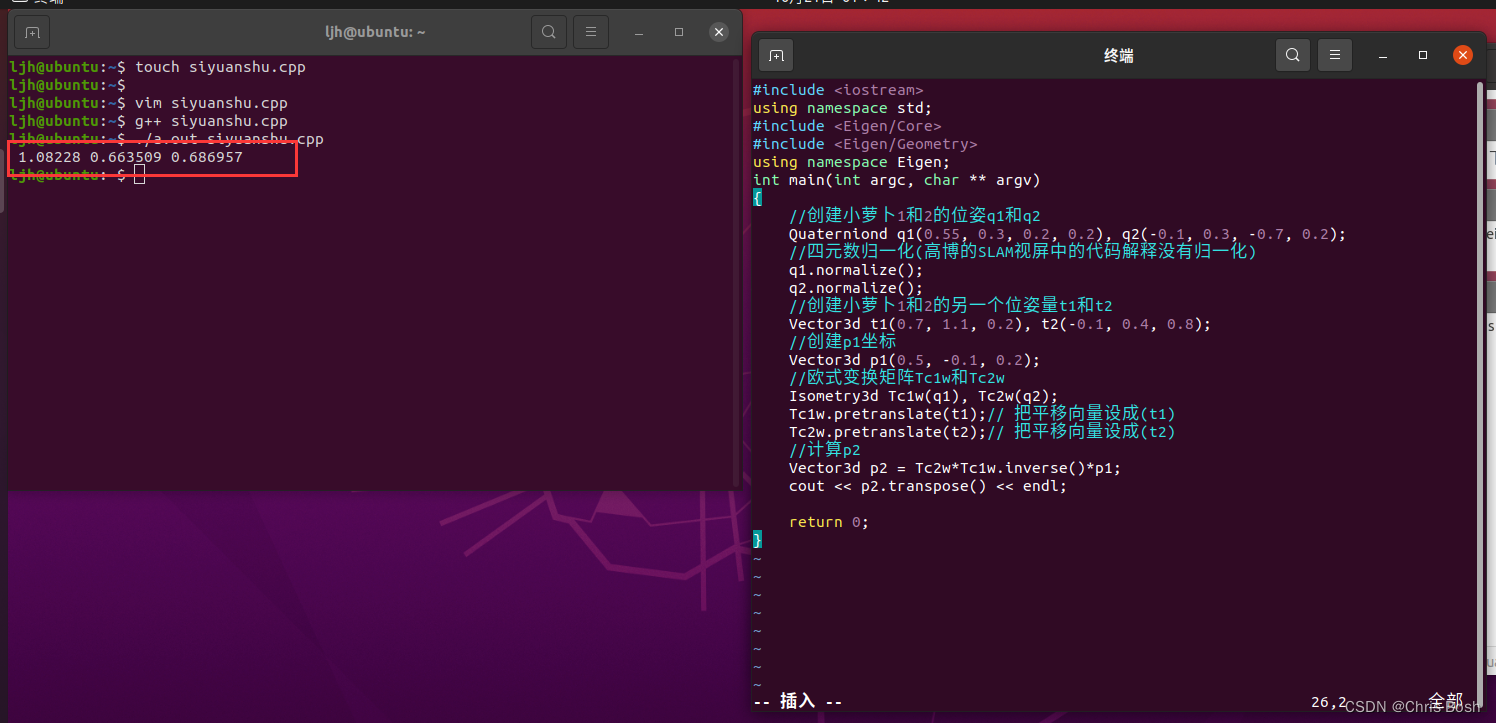
- 参考答案为 p2 = [1:08228; 0:663509; 0:686957]T。你可以⽤它验证程序是否正确。
#include <iostream>
using namespace std;
#include <Eigen/Core>
#include <Eigen/Geometry>
using namespace Eigen;
int main(int argc, char ** argv)
{
//创建小萝卜1和2的位姿q1和q2
Quaterniond q1(0.55, 0.3, 0.2, 0.2), q2(-0.1, 0.3, -0.7, 0.2);
//四元数归一化(高博的SLAM视屏中的代码解释没有归一化)
q1.normalize();
q2.normalize();
//创建小萝卜1和2的另一个位姿量t1和t2
Vector3d t1(0.7, 1.1, 0.2), t2(-0.1, 0.4, 0.8);
//创建p1坐标
Vector3d p1(0.5, -0.1, 0.2);
//欧式变换矩阵Tc1w和Tc2w
Isometry3d Tc1w(q1), Tc2w(q2);
Tc1w.pretranslate(t1);// 把平移向量设成(t1)
Tc2w.pretranslate(t2);// 把平移向量设成(t2)
//计算p2
Vector3d p2 = Tc2w*Tc1w.inverse()*p1;
cout << p2.transpose() << endl;
return 0;
}
运行结果如下,我们可以看到答案正确:
Eigen/四元数的语法规则,及其用法参考如下:
#include <iostream>
#include <cmath>
using namespace std;
#include <Eigen/Core>
// Eigen 几何模块
#include <Eigen/Geometry>
/****************************
* 本程序演示了 Eigen 几何模块的使用方法
****************************/
int main ( int argc, char** argv )
{
// Eigen/Geometry 模块提供了各种旋转和平移的表示
// 3D 旋转矩阵直接使用 Matrix3d 或 Matrix3f
Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();
// 旋转向量使用 AngleAxis, 它底层不直接是Matrix,但运算可以当作矩阵(因为重载了运算符)
Eigen::AngleAxisd rotation_vector ( M_PI/4, Eigen::Vector3d ( 0,0,1 ) ); //沿 Z 轴旋转 45 度
cout .precision(3);
cout<<"rotation matrix =\n"<<rotation_vector.matrix() <<endl; //用matrix()转换成矩阵
// 也可以直接赋值
rotation_matrix = rotation_vector.toRotationMatrix();
// 用 AngleAxis 可以进行坐标变换
Eigen::Vector3d v ( 1,0,0 );
Eigen::Vector3d v_rotated = rotation_vector * v;
cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
// 或者用旋转矩阵
v_rotated = rotation_matrix * v;
cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
// 欧拉角: 可以将旋转矩阵直接转换成欧拉角
Eigen::Vector3d euler_angles = rotation_matrix.eulerAngles ( 2,1,0 ); // ZYX顺序,即roll pitch yaw顺序
cout<<"yaw pitch roll = "<<euler_angles.transpose()<<endl;
// 欧氏变换矩阵使用 Eigen::Isometry
Eigen::Isometry3d T=Eigen::Isometry3d::Identity(); // 虽然称为3d,实质上是4*4的矩阵
T.rotate ( rotation_vector ); // 按照rotation_vector进行旋转
T.pretranslate ( Eigen::Vector3d ( 1,3,4 ) ); // 把平移向量设成(1,3,4)
cout << "Transform matrix = \n" << T.matrix() <<endl;
// 用变换矩阵进行坐标变换
Eigen::Vector3d v_transformed = T*v; // 相当于R*v+t
cout<<"v tranformed = "<<v_transformed.transpose()<<endl;
// 对于仿射和射影变换,使用 Eigen::Affine3d 和 Eigen::Projective3d 即可,略
// 四元数
// 可以直接把AngleAxis赋值给四元数,反之亦然
Eigen::Quaterniond q = Eigen::Quaterniond ( rotation_vector );
cout<<"quaternion = \n"<<q.coeffs() <<endl; // 请注意coeffs的顺序是(x,y,z,w),w为实部,前三者为虚部
// 也可以把旋转矩阵赋给它
q = Eigen::Quaterniond ( rotation_matrix );
cout<<"quaternion = \n"<<q.coeffs() <<endl;
// 使用四元数旋转一个向量,使用重载的乘法即可
v_rotated = q*v; // 注意数学上是qvq^{-1}
cout<<"(1,0,0) after rotation = "<<v_rotated.transpose()<<endl;
return 0;
}
3.旋转的表达

1. 设有旋转矩阵 R,证明 RT R = I 且 det R = +12。

2. 设有四元数 q,我们把虚部记为ε,实部记为 η,那么 q = (ε,η)。请说明 ε 和 η 的维度。
四元数q有三个虚部和一个实部。
即q=q0+q1i+q2j+q3k
因此ε的维度为3, η的维度为1。
3.第三问

4.罗德里格斯公式的证明
罗德⾥格斯公式描述了从旋转向量到旋转矩阵的转换关系。设旋转向量长度为 θ,⽅向为 n,那么旋转矩阵 R 为:
R = cos θI − (1 − cos θ)nnT + sin θn^. ------------------------------------------------------------(4)
我们在课程中仅指出了该式成⽴,但没有给出证明。请你证明此式。

参考:
链接: 罗德里格斯公式的证明
5.四元数运算性质的验证


6.熟悉 C++11
请注意本题为附加题。 C++ 是⼀门古⽼的语⾔,但它的标准⾄今仍在不断发展。在 2011 年、 2014 年和 2017 年, C++的标准又进⾏了更新,被称为 C++11, C++14, C++17。其中, C++11 标准是最重要的⼀次更新,让C++发⽣了重要的改变,也使得近年来的 C++ 程序与你在课本上(⽐如谭浩强)学到的 C++ 程序有很⼤的不同。你甚⾄会惊叹这是⼀种全新的语⾔。 C++14 和 C++17 则是对 11 标准的完善与扩充。
越来越多的程序开始使⽤11 标准,它也会让你在写程序时更加得⼼应⼿。本题中,你将学习⼀些 11标准下的新语法。请参考本次作业 books/⽬录下的两个pdf,并回答下⾯的问题。 设有类 A,并有 A 类的⼀组对象,组成了⼀个 vector。现在希望对这个 vector进⾏排序,但排序的⽅式由 A.index 成员⼤⼩定义。那么,在 C++11 的语法下,程序写成:
1#include <iostream>
2#include <vector>
3#include <algorithm>
4
5 using namespace std;
6
7 class A {
8 public:
9 A(const int& i ) : index(i) {}
10 int index = 0;
11};
12
13 int main() {
14 A a1(3), a2(5), a3(9);
15 vector<A> avec{a1, a2, a3};
16 std::sort(
avec.begin(), avec.end(), [](const A&a1, const A&a2) {return a1.index<a2.index;}
);
17 for ( auto& a: avec ) cout<<a.index<<" ";
18 cout<<endl;
19 return 0;
20 }
请说明该程序中哪些地⽅⽤到了 C++11 标准的内容。提⽰:请关注范围 for 循环、⾃动类型推导、 lambda表达式等内容。
该程序中使用了C++11标准的以下内容:
iostream:使用了C++11中引入的iostream库,用于输入输出流操作。
vector:使用了C++11中引入的vector容器,用于存储和操作A类的实例。
algorithm:使用了C++11中引入的algorithm库,其中的sort函数用于对vector容器中的元素进行排序。
using namespace std;:使用了C++11中引入的namespace别名声明,用于简化对std命名空间的使用。
class A:使用了C++11中引入的类初始化列表语法,用于对A类的成员变量进行初始化。
vector avec{a1, a2, a3}; :使用了C++11中引入的列表初始化语法,用于初始化vector容器avec并添加元素。
[] (const A&a1, const A&a2) { return a1.index < a2.index; }:使用了C++11中引入的lambda表达式,用作sort函数的排序准则。其中:const A&a1, const A&a2是参数列表,return a1.index<a2.index;是函数体,返回值是布尔型的大小比较结果。
for (auto& a : avec):使用了C++11中引入的范围for循环语法,用于遍历vector容器avec中的元素。用auto关键字实现了自动类型推导,让编译器自动设置变量a的类型;C++引入了基于范围的for循环,不用下标就能访问元素;








![[尚硅谷React笔记]——第5章 React 路由](https://img-blog.csdnimg.cn/dc3b54d6f48d4ed1aa31eb66454cd7a5.png)