偏振光
- 目录
- 基础概念
- 基础概念的补充
- 平面偏振光(线偏振光)
- 部分偏振光
- 圆偏振光
- 椭圆偏振光
- 菲涅耳公式
- 相位关系
- 反射折射所引起的偏振态的改变
- 斯托克斯倒逆关系
- 重要参数
目录
基础概念
- 光是横波:光是电磁波,其电场分量(电场强度)E、磁场分量(磁感应强度)B都与光的传播方向(用波矢k表示)垂直,所以光波是横波.(P62)
- 偏振:振动方向相对于传播方向的不对称性(P62)
- 二向色性:只有振动方向和透振方向一致的光才能从晶体透射
- 起偏:通过某种方法或使用某种光学元件,使光变为具有偏振特性.
- 检偏:检偏通过某种方法或使用某种光学元件,检验光的偏振特性.
- 透偏方向:透振方向从偏振器件通过的光的电矢量的振动方向.例如,上述金属线栅中垂直于金属丝的方向就是透振方向.
- 超声波:超出人正常能听到的频率的声波
- 自然光通过起偏器后,如果不考虑起偏器对光强的吸收,则透射光强为入射光强的一半.
基础概念的补充
证明光是横波的两种方法
- 双散射实验
- 二向色性晶体透射实验
光波和其他的波的区别
- 比普通的电磁波和机械波频率要高的多
- 不可控,是通过原子或者离子跃迁自发进行的
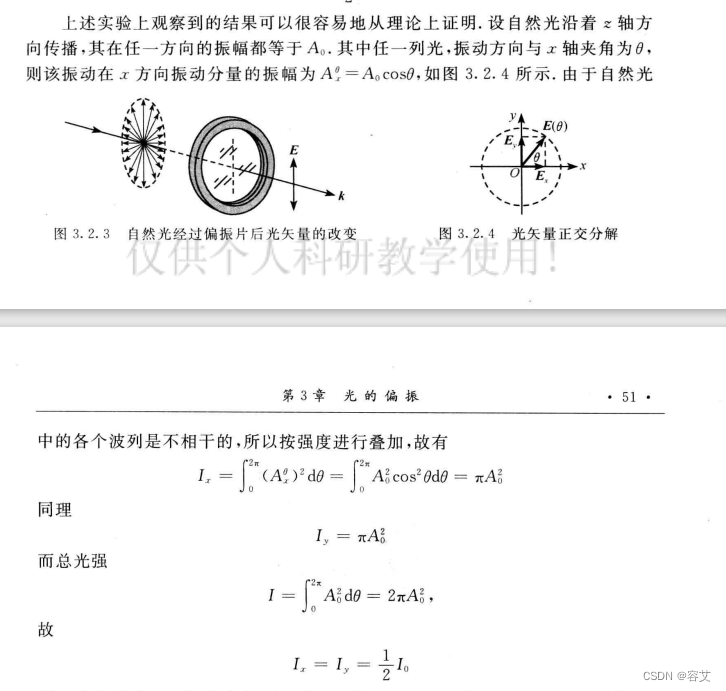
证明:自然光通过起偏器后,如果不考虑起偏器对光强的吸收,则透射光强为入射光强的一半.
平面偏振光(线偏振光)
概念
自然光经过起偏器(二向色性晶体、偏振片等)后,由于只有平行于起偏器透振方向的电矢量能够通过,因而透射光只包含单一振动方向的电矢量.这种电矢量始终在一个平面内振动的光,或者电矢量振动的投影是一条直线的光,就是平面偏振光(plane-polarized light)或线偏振光(linearly polarized light).
马吕斯定律
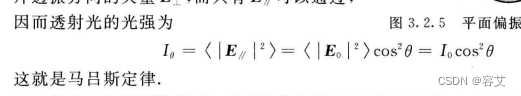
其中,如果使平面偏振光垂直地射向偏振片,而该偏振片的透振方向与入射光的偏振平面之间的夹角为ɵ
部分偏振光
概念
如果光的偏振特性介于自然光和线偏光之间,则被称作部分偏振光
偏振度
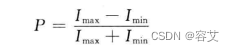
其中,用偏振片检验透过的光强,则在某个方向,透射光强最大,记为Imax ;在与其垂直的方向,透射光强最小,记为Imin.
结果分析:偏振度0≤P≤1.如果Imax=Imim ,就是自然光,即每个方向都一致,偏振度P=0;如果Imin=0,就是平面偏振光,偏振度P=1,即于平面偏振光方向垂直光强为0.
圆偏振光
概念
圆偏振光正确的物理图像应该这样描述:在一个与波矢垂直的固定平面内,其光矢量(电矢量)以固定的角速度绕波矢旋转.
分解为两个平面偏振光
由波的矢量叠加可以判断,圆偏振光可以分解为两个振幅相等的相互垂直的平面偏振光,这两个平面偏振光具有Π/2的相位差,分解后场强表示为:
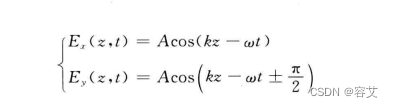
其中k是波长的倒数,w是角速度
椭圆偏振光
概念
与圆偏振光相比,旋转时光矢量数值变化如椭圆
正交分解

椭圆长轴或短轴与坐标轴的夹角为

计算方法:先转化为标准形式,再按照下列公式计算

椭圆旋转方向


联系

例题

计算方法:将偏振光分解为两个平面偏振光,并假设光强最大透射方向为椭圆长轴方向,计算光强投影分量即可
菲涅耳公式
数学表达式

透射率和反射率

3.3.5等式的转换方式是根据根据斯涅尔定律(Snell’s Law)进行转化,即折射角和入射角之间的关系可以由下式给出:
n1 * sin(θ1) = n2 * sin(θ2)
能流透射率

相位关系
折射角

反射角

结论:

反射折射所引起的偏振态的改变
垂直入射

布儒斯特定律
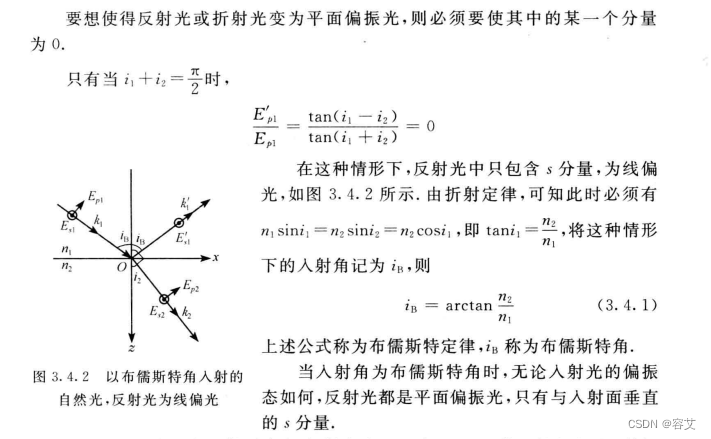
例题3.4.2总结
- 折射光振幅计算是根据i1+i2=Π/2转换
- 光强其实就是振幅的平方乘以透射率
- 折射光的偏振度就是比较两个分量,相当于是椭圆
折射光变为偏振光
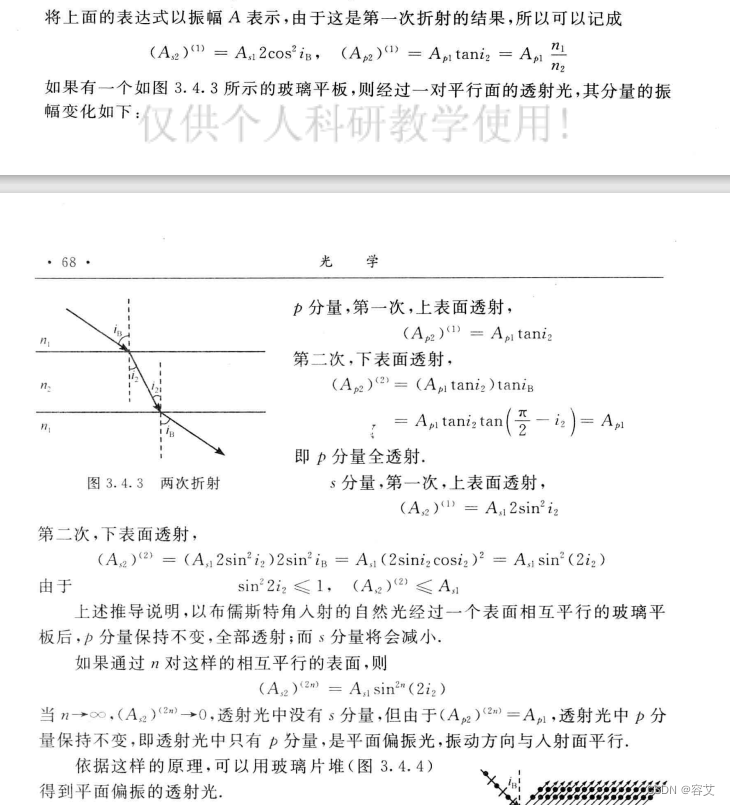
布儒斯特窗

斯托克斯倒逆关系

重要参数
消光比
消光比=最小透射光强/最大透射光强
其中,透射光强的计算用马吕斯定律






![【蓝桥每日一题]-动态规划 (保姆级教程 篇10)#方格取数](https://img-blog.csdnimg.cn/95fb4873352b469c9cc7b05c2746ebb8.png)