文章目录
- 背景
- 输入点
- 直接输入邻接矩阵
背景
网上倒是有一些关于使用sklearn进行谱聚类的教程,但是这些教程的输入都是一些点的集合,然后根据谱聚类的原理,其会每两个点计算一次亲密度(可以认为两个点距离越大,亲密度越小),假设一共有N个点,那么就是N*N个亲密度要计算,这特别像什么?图里面的邻接矩阵对不对。然后算法再根据这些亲密度进行聚类,即亲密度越大的点,他们应该聚在一起。
总结,这些教程都是输入点,没有说如何直接输入邻接矩阵,然后使用sklearn进行谱聚类。
输入点
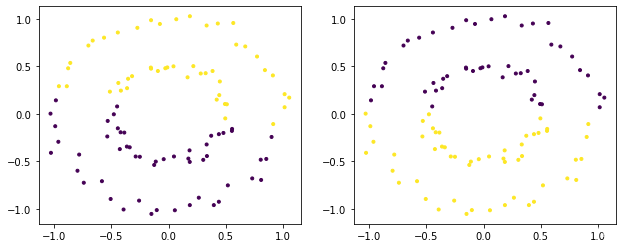
下面的X就是输入的点的坐标,形状为(100,2),我们是对这些点进行聚类,聚两类。然后affinity参数其实就是距离计算公式你选用哪个的意思,比如我们常常知道的欧式距离,曼哈顿距离,当然谱聚类里面不是这些。总之,实际使用中,哪个效果好用哪个,建议官方提供的距离你都可以试一试。
import numpy as np
from sklearn import datasets
from sklearn.cluster import SpectralClustering
import matplotlib.pyplot as plt
X, _ = datasets.make_circles(n_samples=100, factor=0.5, noise=0.05)
#X就是输入的点
fig = plt.figure(figsize=(16,4))
# 谱聚类默认聚类数为8
model = SpectralClustering(n_clusters=2).fit(X)
ax = fig.add_subplot(132)
ax.scatter(X[:,0], X[:,1], c=model.labels_, marker='.')
model = SpectralClustering(n_clusters=2, affinity="nearest_neighbors").fit(X)
ax = fig.add_subplot(133)
ax.scatter(X[:,0], X[:,1], c=model.labels_, marker='.')
plt.show()
直接输入邻接矩阵
邻接矩阵表示各个点之间的亲密度,我们先准备好邻接矩阵如下,形状是N*N,注意邻接矩阵需要为正数,否则报错,所以我们下面用了指数。
adjacency_matrix=[[ 0.0470, 0.0309, 0.0269, 0.0867, 0.0548, 0.0109, 0.0771, 0.0307,
0.0276],
[ 0.1033, 0.0157, 0.0012, -0.0097, 0.0050, 0.0059, -0.0179, -0.0133,
-0.0074],
[-0.0070, 0.0795, 0.0222, -0.0379, -0.0281, -0.0073, -0.0569, -0.0341,
-0.0208],
[ 0.0370, 0.0165, -0.0008, 0.0012, -0.0044, -0.0090, 0.0311, 0.0330,
0.0124],
[-0.0185, -0.0267, -0.0199, 0.1049, 0.0289, -0.0023, -0.0270, -0.0290,
-0.0348],
[-0.1064, -0.0719, -0.0368, -0.0589, 0.0236, -0.0024, -0.0903, -0.0769,
-0.0512],
[ 0.0624, 0.0479, 0.0304, 0.0762, 0.0512, 0.0178, 0.0633, 0.0288,
0.0256],
[-0.0258, -0.0148, -0.0024, -0.0092, 0.0007, -0.0081, 0.0819, -0.0039,
-0.0092],
[-0.0472, -0.0152, -0.0039, -0.0405, -0.0287, -0.0161, -0.0083, 0.0608,
-0.0053]]
adjacency_matrix=np.exp(np.array(adjacency_matrix))
from sklearn.cluster import SpectralClustering
sc = SpectralClustering(3, affinity='precomputed', n_init=100,
assign_labels='discretize')#precomputed就是说我们算好了的意思。
sc.fit_predict(adjacency_matrix)
输出结果
array([1, 2, 2, 1, 0, 0, 1, 1, 0], dtype=int64)
这个就是我们9个点的聚类结果。