操作环境：

MATLAB 2022a

1、算法描述

​1.白鲸优化算法（WOA）： 白鲸优化算法是一种受白鲸捕食行为启发的优化算法。该算法模拟了白鲸群体捕食的策略和行为，用以寻找问题的最优解。其基本思想主要包括以下几点：

    -位置表示：将问题的解表示成白鲸在搜索空间中的位置，每个位置代表解的一个候选解。

    -捕食行为：白鲸通过跟踪和围捕猎物来寻找最优解，模拟了其在水中的移动和捕食行为。

    -群体合作：白鲸通过群体合作来提高捕食效率，这在算法中体现为信息的共享和个体间的相互影-响。搜索更新：根据当前最优解和个体之间的相对位置，更新白鲸的位置，进而寻找更好的解。

    -迭代优化：重复进行捕食行为和位置更新的过程，逐步提升解的质量，直至达到满意的解或者满足终止条件。

2. 遗传算法：

遗传算法是一种模拟自然选择和遗传机制的优化算法。它模拟了生物种群的进化过程，用于寻找问题的最优解。其基本思想包括：
   - 个体表示：将问题的解表示成一组基因，每个基因对应解的一个特征或者参数。
   - 适应度评估：根据问题的目标函数，评估每个个体的适应度，适应度越高代表解越好。
   - 选择：根据适应度，以一定的概率选择一些个体作为父代，用于产生下一代。
   - 交叉和变异：通过交叉和变异操作，将父代的基因组合并产生新的个体，引入新的遗传信息。
   - 进化迭代：重复进行选择、交叉和变异的过程，逐步优化解的质量，直至达到满意的解

3. 栅格路径规划：
   栅格路径规划是一种常用于自动导航和机器人运动控制的方法。它将环境划分成一个个小方格，每个方格称为栅格。每个栅格可以被认为是地图上的一个单元，可以是可通行的区域或者障碍物。这种方法的主要步骤包括：
   - 地图建模：将环境抽象成一个二维栅格地图，其中包括了可通行区域和障碍物。
   - 路径搜索：使用搜索算法（如A*算法）在栅格地图上寻找一条从起点到目标点的最优路径，最优通常是指最短路径或者最快到达目标。
   - 路径优化：对于复杂环境或者特殊要求，可能需要进行路径的后处理或者优化，以确保路径的可行性和高效性。

2、仿真结果演示

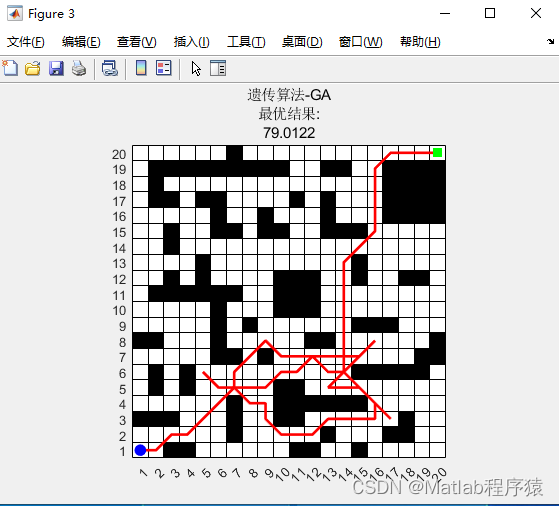
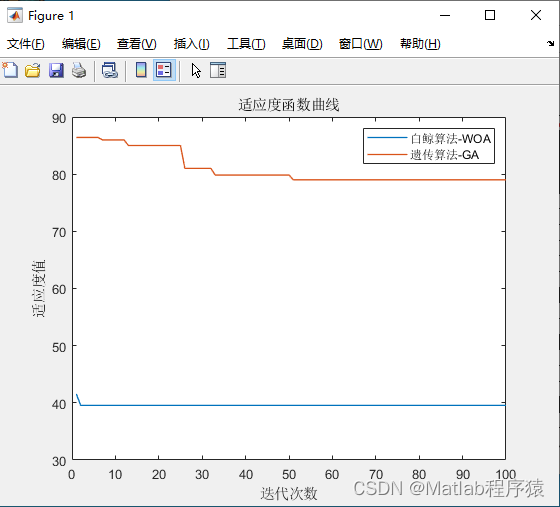
3、关键代码展示

略

4、MATLAB 源码获取

      V

点击下方名片