散列表：如何打造一个工业级水平的散列表？

文章来源于极客时间前google工程师−王争专栏。

散列表的查询效率并不能笼统地说成是O(1)。它跟散列函数、装载因子、散列冲突等都有关系。如果散列函数设计得不好，或者装载因子过高，都可能导致散列冲突发生的概率升高，查询效率下降。

极端情况下，某些恶意攻击者，可能通过精心构造的数据，使得所有数据经过散列函数之后，都散列到同一个槽里。如果我们使用的是基于链表的冲突解决办法，那这个时候，散列表就会退化为链表，查询的时间复杂度就从O(1)退化为O(n)。

如果散列表中有10万个数据，退化后的散列表查询效率就下降了10万倍。这样可能因为查询操作消耗大量CPU或者线程资源，导致系统无法响应其他请求，从而达到拒绝服务攻击（DOS）的目的。这也就是散列表碰撞攻击的基本原理。

问题：如何设计一个可以应对各种异常情况的工业级散列表，来避免在散列冲突的情况下，散列表性能的急剧下降，并且能抵抗散列碰撞攻击？

如何设计散列函数？

散列函数设计的好坏，决定了散列表冲突的概率大小，也直接决定了散列表的性能。

第一，散列函数的设计不能太复杂。过于复杂的散列函数，势必会消耗很多计算时间，也就间接影响到散列表的性能。

第二，散列函数生成的值要尽可能随机并且均匀分布。这样才能避免或者最小化散列冲突，即便出现冲突，散列到每个槽里的数据也会比较平均，不会出现某个槽内数据特别多的情况。

学生运动会中，参赛编号后两位作为散列值。散列函数处理手机号，手机号码前几位重复的可能性很大，后面几位比较随机，可以取手机号的后四位作为散列值。这种散列函数的设计方法，我们一般叫作“数据分析法”。

如何实现Word拼写检查功能。散列函数可以这样设计：将单词中每个字母的ASCII码值“进位”相加，然后再跟散列表的大小求余、取模，作为散列值。比如英文单词nice，通过散列函数转化的散列值就是：

hash("nice")=(("n" - "a") * 26*26*26 + ("i" - "a")*26*26 + ("c" - "a")*26+ ("e"-"a")) / 78978

散列函数的设计方法包括直接寻址法、平方取中法、折叠法、随机数法，需要了解。

装载因子过大了怎么办？

装载因子越大，说明散列表中的元素越多，空闲位置越少，散列冲突的概率就越大。不仅插入数据的过程要多次寻址或者拉很长的链，查找的过程也会变得很慢。

动态散列表，数据集合是频繁变动。

针对散列表，当装载因子过大时，可以进行动态扩容，重新申请一个更大的散列表，将数据搬移到这个新散列表中。装载因子也会折半。

针对数组的扩容，数据搬移操作比较简单。但是，针对散列表的扩容，数据搬移操作要复杂很多。因为散列表的大小变了，数据的存储位置也变了，我们需要通过散列函数重新计算每个数据存储的位置。

如下图所示，在原散列表中，21这个元素原来存储在下标为0的位置，搬移到新的散列表中，存储在下标为7的位置。

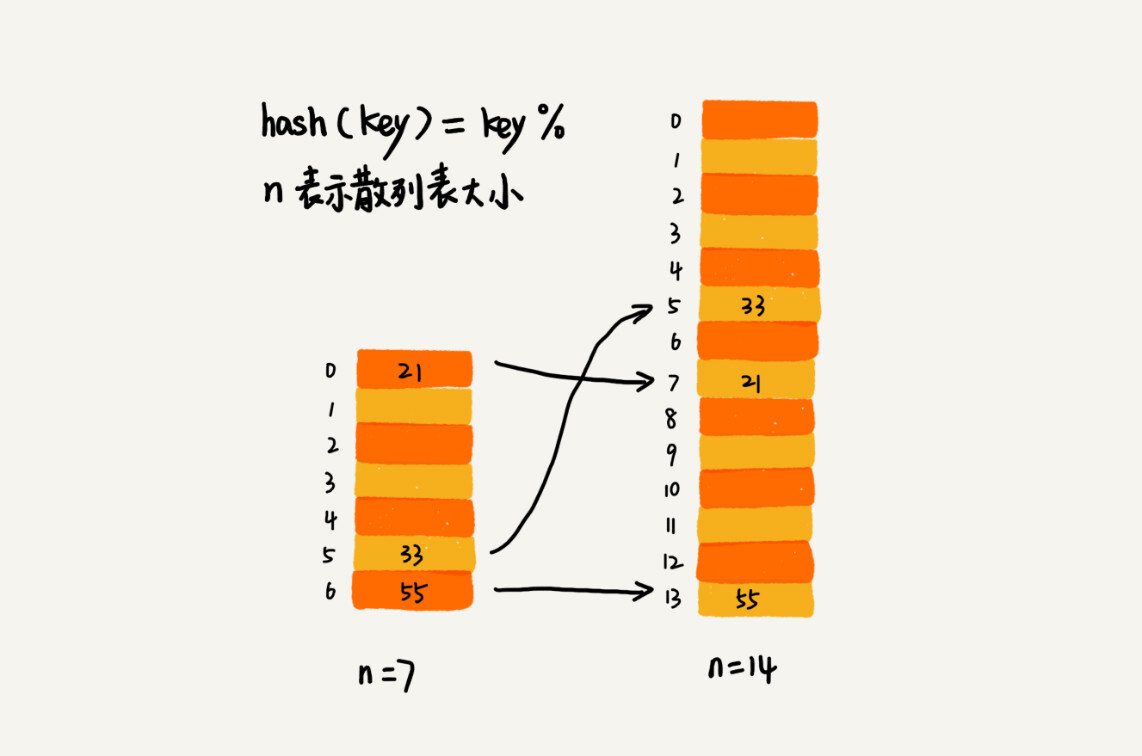
需要复习：动态扩容数组、栈等数据结构的时间复杂度。

插入一个数据：

最好：O(1)
最坏：散列因子过高，启动扩容，重新申请内存空间，重新计算哈希位置，搬移数据，时间复杂度是O(n)
平均：均摊情况下，时间复杂度接近最好情况，就是O(1)

如果内存紧张，对于动态散列表，随着数据的删除，空闲空间会越来越多。我们可以在装载因子小于某个值之后，启动动态缩容。

装载因子阈值需要选择得当。如果太大，会导致冲突过多；如果太小，会导致内存浪费严重。

如何避免低效地扩容？

问题：当装载因子已经到达阈值，需要先进行扩容，再插入数据。这个时候，插入数据就会变得很慢，甚至无法接受。

比如说，如果散列表当前大小为1GB，要想扩容为原来的两倍大小，那就需要对1GB的数据重新计算哈希值，并且从原来的散列表搬移到新的散列表，听起来就很耗时！

如果我们的业务代码直接服务于用户，尽管大部分情况下，插入一个数据的操作都很快，但是极个别非常慢的插入操作，也会让用户崩溃。这个时候，“一次性”扩容的机制就不合适了。

解决办法：将扩容操作穿插在插入操作的过程中，分批完成。当装载因子触达阈值之后，我们只申请新空间，但并不将老的数据搬移到新散列表中。

通过这样的均摊方法，将一次性扩容的代价，均摊到多次插入操作中，就避免了一次性扩容耗时过多的情况。这种实现方式，任何一种情况下，插入一个数据的时间复杂度都是O(1)。

如何选择冲突解决办法？

散列冲突主要有两种解决办法，开放寻址法和链表法。这两种解决办法在实际的软件开发中都非常常用。比如，java中LinkedHashMap就采用了链表法解决冲突，ThreadLocalMap是通过线性探测的开放寻址法来解决冲突。这两种冲突解决方法各自有什么优势和劣势，又各自适用哪些场景？

1.开放寻址法

开放寻址法的优点：

散列表中的数据都存储在数组中，可以有效地利用CPU缓存加快查询速度。而且这种方法实现的散列表，序列化起来比较简单。链表法包含指针，序列化起来就没那么容易。什么是数据结构序列化？如何序列化？为什么要序列化？

开放寻址法的缺点：

开放寻址法解决冲突的散列表，删除数据比较麻烦，需要特殊标记已经删掉的数据。在开放寻址法中，所有的数据都存储在一个数组中，比起链表法来说，冲突的代价更高。所以，使用开放寻址法解决冲突的散列表，装载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。

总结：当数据量比较小、装载因子小的时候，适合采用开放寻址法。这是java中的ThreadLocalMap使用开放寻址法解决散列冲突的原因。

2.链表法

链表法对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建，并不需要像开放寻址法那样事先申请好。实际上，这一点也是链表优于数组的地方。

开放寻址法只适用装载因子小于1的情况。接近1时，就可能会有大量的散列冲突，导致大量的探测、再散列等，性能会下降很多。但对于链表法来说，只要散列函数的值随机均匀，即便装载因子变成10，也只是链表的长度边长而已，虽然查找效率有所下降，但是比起顺序查找还是快很多。

链表因为要存储指针，所以对于比较小的对象（大对象指针内存占用可以忽略）的存储，是比较消耗内存的，还有可能让内存的消耗翻倍。链表中的结点是零散分布在内存中的，不是连续的，所以对CPU缓存是不友好的，这方面对于执行效率也有影响。

对链表法稍加改造，可以实现一个更加高效的散列表。我们将链表法中的链表改造为其他高效的动态数据结构，比如跳表、红黑树。这样，即便出现散列冲突，极端情况下，所有数据都散列到同一个桶内，那最终退化的散列表的查找时间也只不过是O(logn)。这样就有效避免了前面说的散列碰撞攻击。

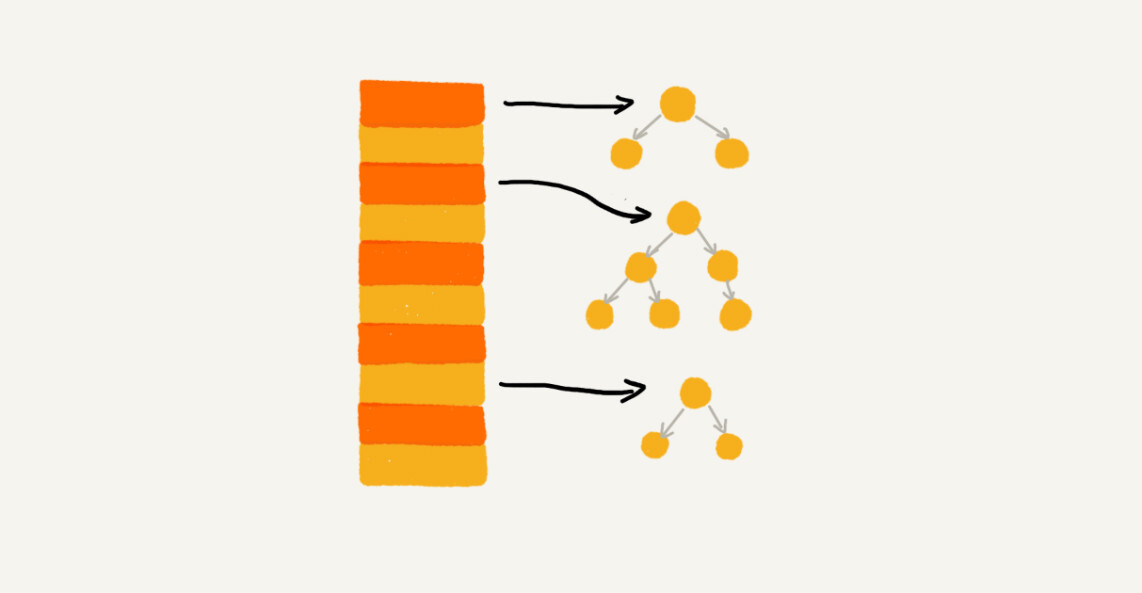
总结：基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表，而且比起开放寻址，它更加灵活，支持更多的优化策略，比如用红黑树代替链表。

工业级散列表举例分析

java中的HashMap

1.初始大小

HashMap的默认初始大小是16，当然这个默认值是可以设置的，如果事先知道大概的数据量有多大，可以通过修改默认初始大小，减少动态扩容的次数，这样会大大提高HashMap的性能。

2.装载因子和动态扩容

最大装载因子默认是0.75，当HashMap中元素个数超过0.75*capacity（散列表的容量），就会启动扩容，每次扩容都为原来的两倍大小。

3.散列冲突解决方法

HashMap底层采用链表法来解决冲突。即使负载因子和散列函数设计的再合理，也免不了会出现拉链过长的情况，一旦出现拉链过长，会严重影响HashMap的性能。

于是，在JDK1.8版本中，为了对HashMap做进一步优化，引入红黑树。当链表长度太长（默认超过8）时，链表就装换为红黑树，利用红黑树快速增删改查的特点，提高HashMap的性能。当红黑树结点个数少于8个的时候，又会将红黑树转化为链表。因为在数据量较小的情况下，红黑树要维护平衡，比起链表，性能上优势不明显。

4.散列函数

散列函数追求简单高效、分布均匀。

int hash(Object key) {
    int h = key.hashCode()；
    return (h ^ (h >>> 16)) & (capitity -1); //capicity 表示散列表的大小
}

hashCode()返回的是java对象的hash code。比如String类型的对象的hashCode()如下：

public int hashCode() {
  int var1 = this.hash;
  if(var1 == 0 && this.value.length > 0) {
    char[] var2 = this.value;
    for(int var3 = 0; var3 < this.value.length; ++var3) {
      var1 = 31 * var1 + var2[var3];
    }
    this.hash = var1;
  }
  return var1;
}