题目

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数

思路

首先，要明白本题不能使用双指针或者滑动窗口，因为双指针和滑动窗口使用的一个必要条件就是能一步一步迭代，确定窗口的收缩方向，这有负数，就完全不知道是左边缩小，还是右边缩小了，因为nums[i]可以小于0，也就是说右指针i向后移1位不能保证区间会增大，左指针j向后移1位也不能保证区间和会减小。

二者的区别：

（1）滑动窗口：

• 右指针平稳移动，左指针视情况移动。右先行，左视定。
• 多数情况下可以先对数组进行排序处理；
• 循环条件以及边界条件一定要处理好；
• 对于负数，滑动窗口处理不好，左右摇摆了，不知道往那边走了。

（2）前缀和：

• 当循环到 i 时，往往需要前 i-1项 的和来处理；
• 多数结合HashMap ，不要重复就HashSet。

思路 ： 前缀和 + 哈希表

本题是一道经典的前缀和运用题

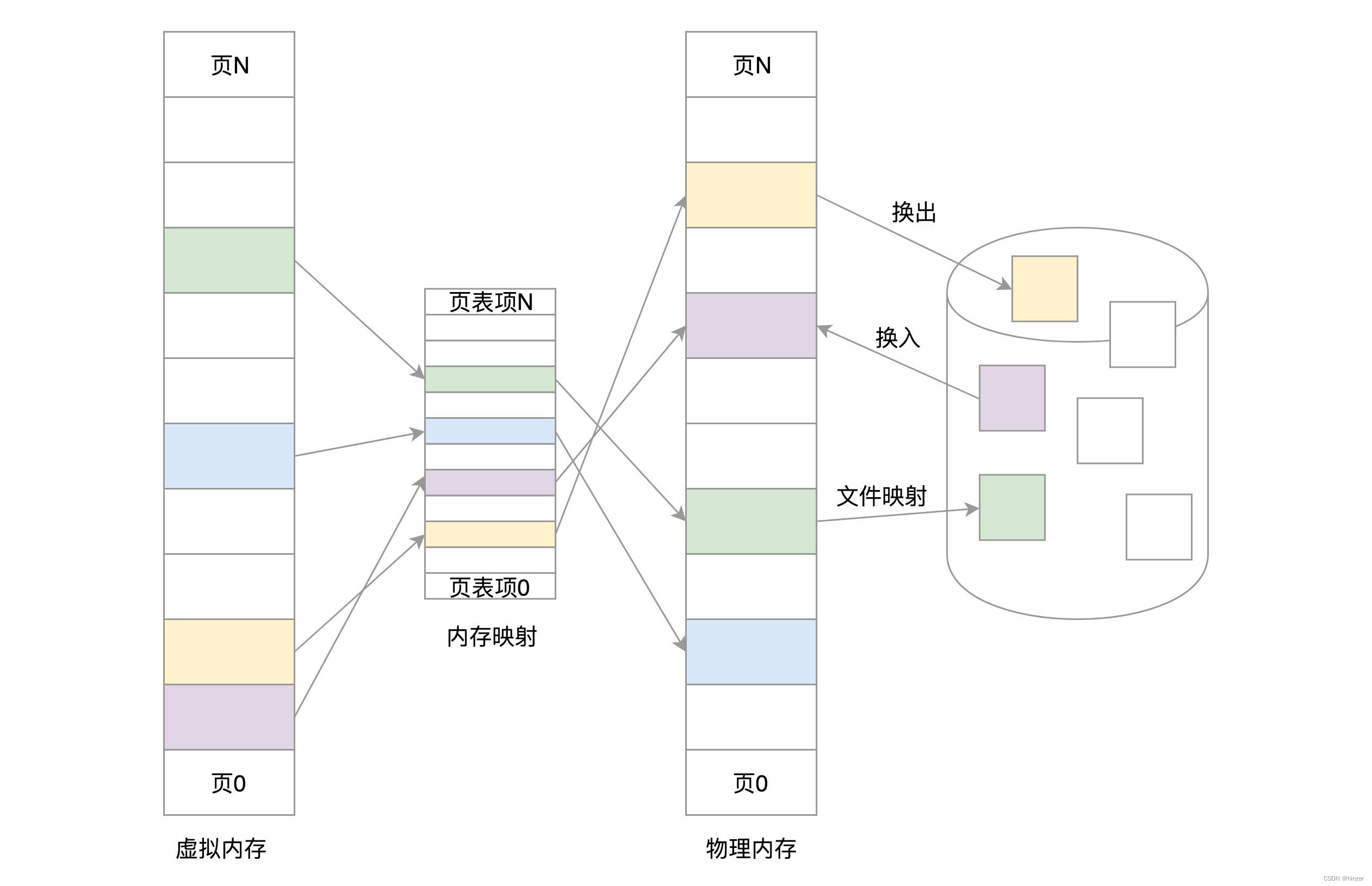
定义 pre[i] 为 [0..i]里所有数的和，则 pre[i]可以由 pre[i−1]递推而来，即：

• pre[i] = pre[i−1] + nums[i]，

那么「[j..i]这个子数组和为 k 」这个条件可以转化为

• pre[i] − pre[j−1] == k

（因为pre[i]表示 [0..i]的和，pre[j−1]表示 [0..j-1]的和，则pre[i] − pre[j−1]表示 [0..i] - [0..j-1] = [j..i]的和）

简单移项可得符合条件的下标 j需要满足

• pre[j−1] == pre[i] − k

所以考虑以i结尾的和为 k 的连续子数组个数时只要统计有多少个前缀和为 pre[i]−k的 pre[j]即可。

建立哈希表 map，以和为键，出现次数为对应的值，记录 pre[i]出现的次数，从左往右边更新 map，那么以 i 结尾的答案 map[pre[i]−k]即可在 O(1) 时间内得到。最后的答案即为所有下标结尾的和为 k 的子数组个数之和。

算法流程图如下：

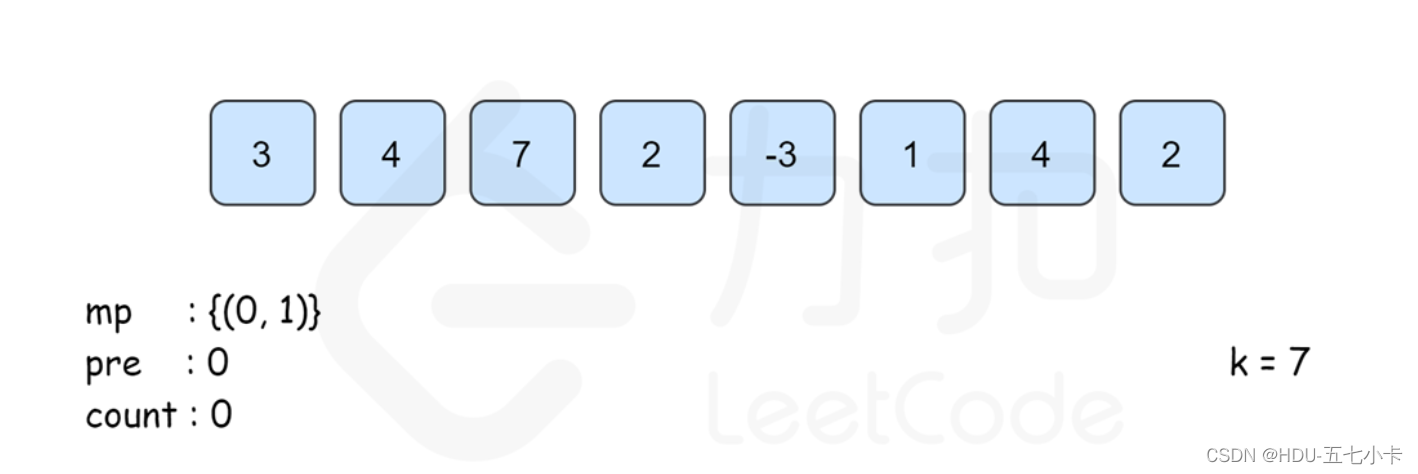
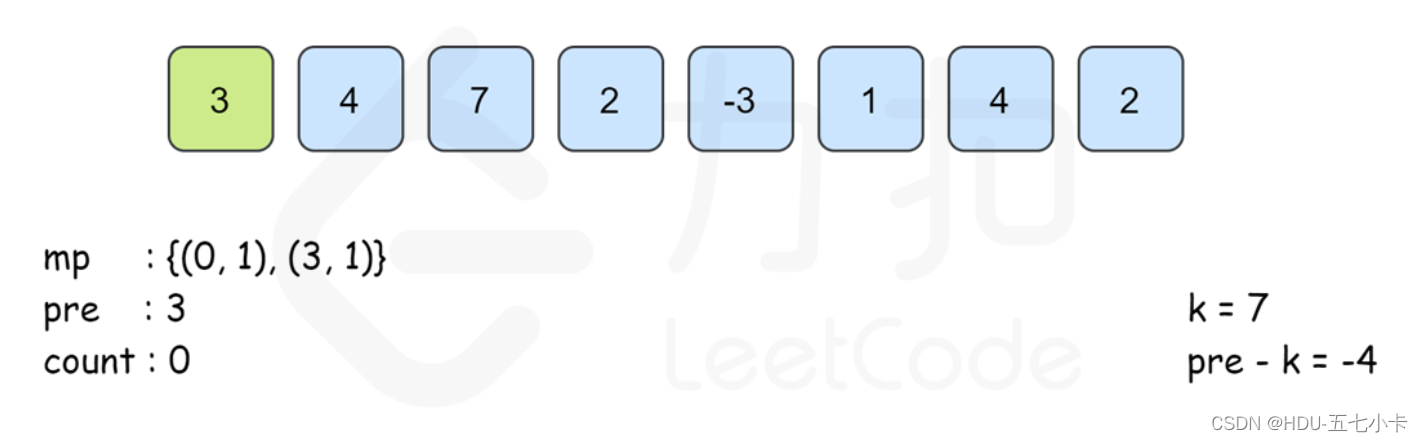
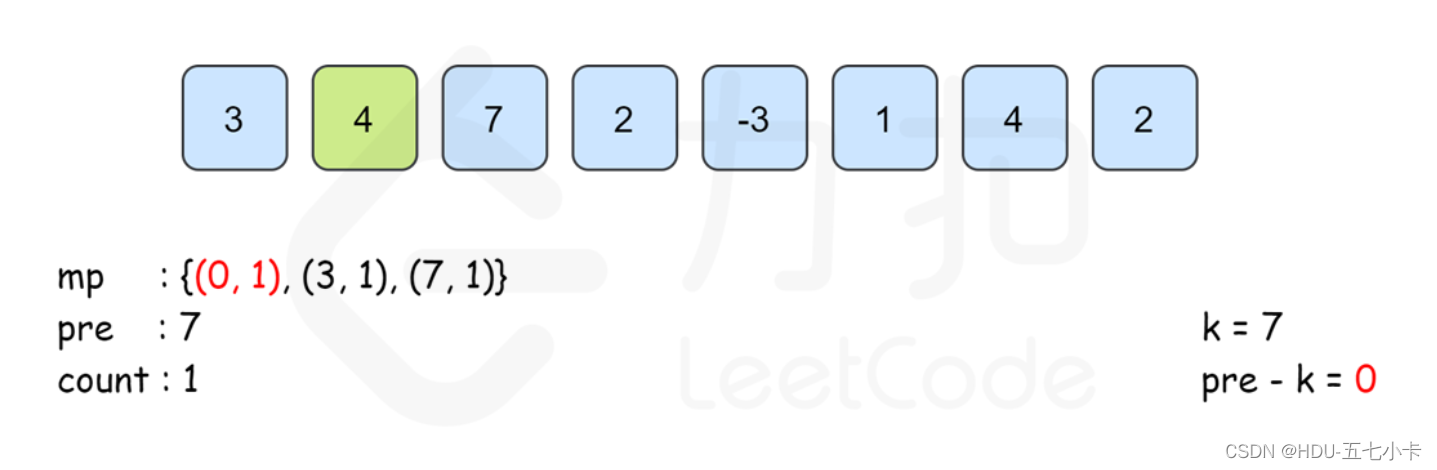
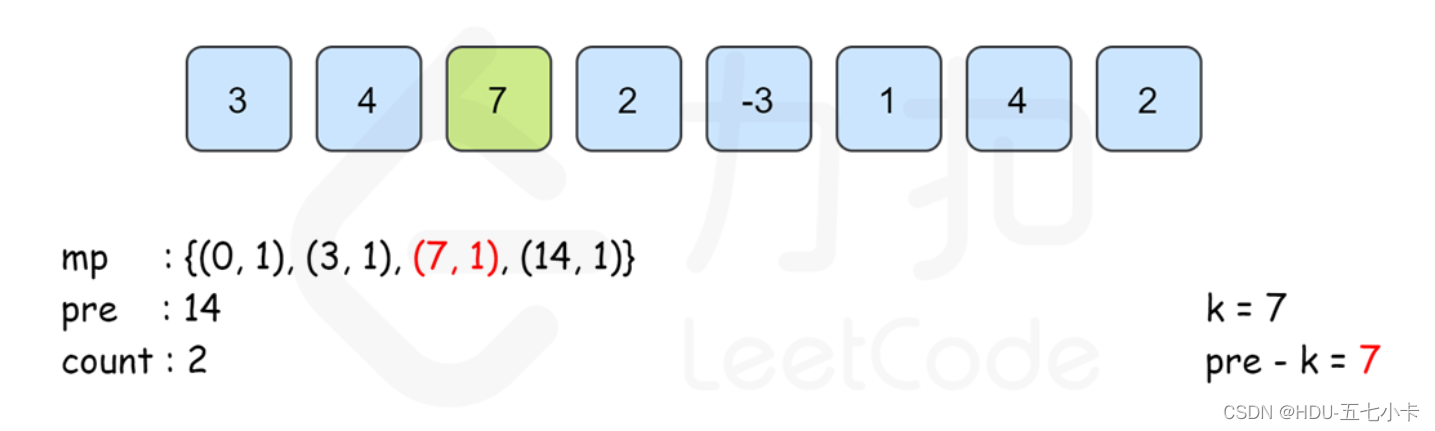
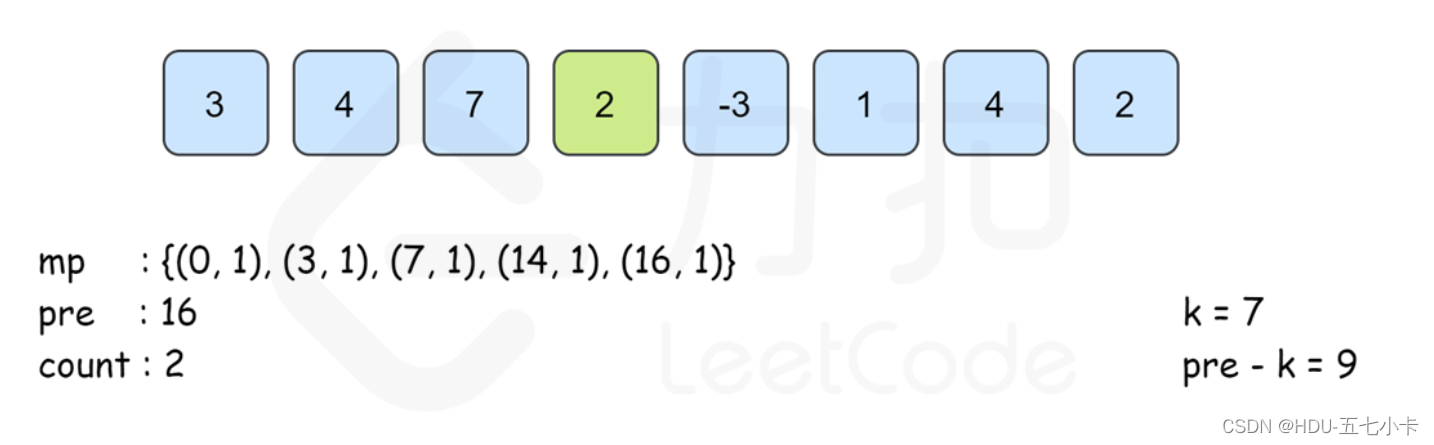
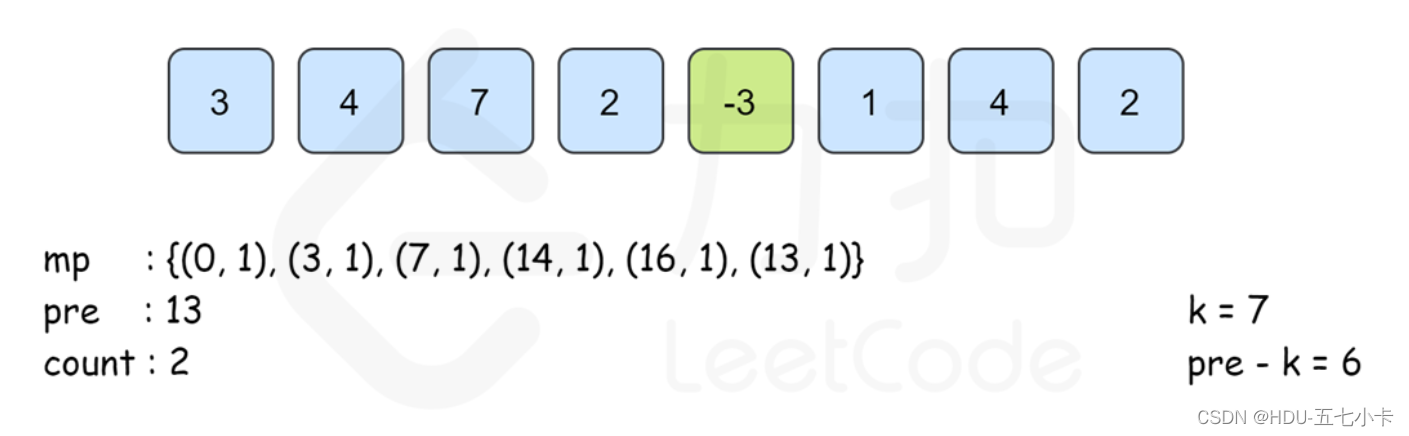
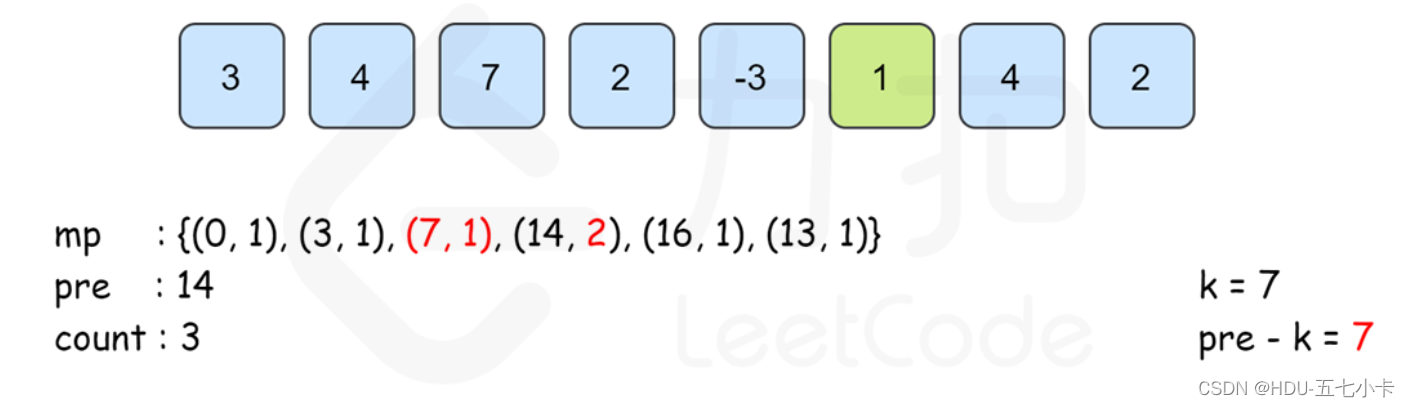
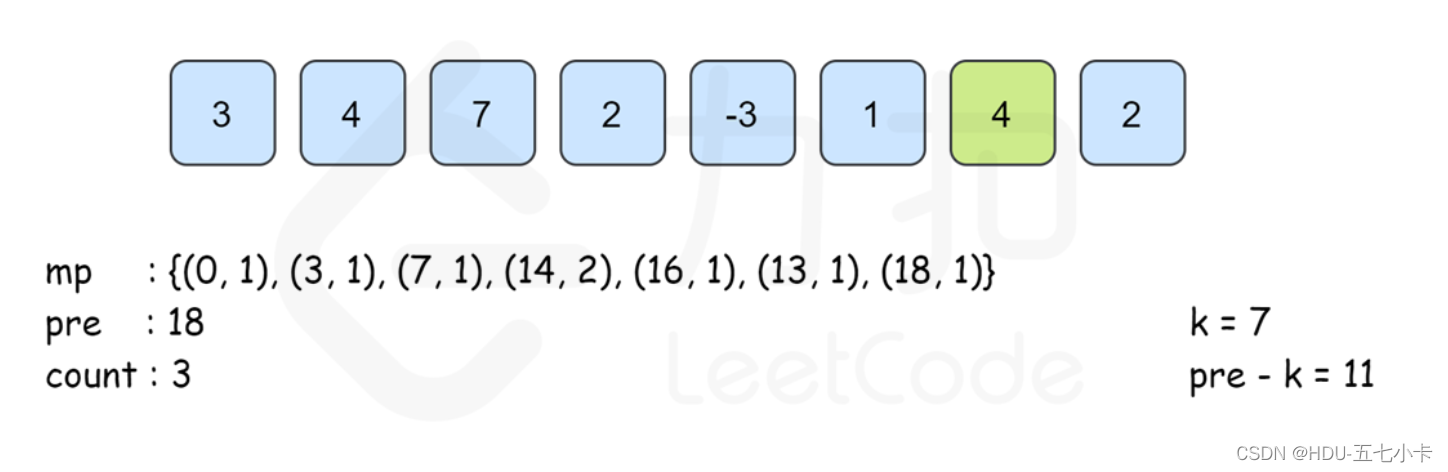
PS:需要注意的是，从左往右边更新边计算的时候已经保证了map[pre[i]−k]里记录的 pre[j]的下标范围是 0≤j≤i。同时， 由于pre[i]的计算只与前一项的答案有关 ，因此可以不用建立 pre数组，直接用 pre变量来记录 pre[i−1]的答案即可

java代码如下：

class Solution {
	public int subarraySum(int[] nums ,int k){
		int count = 0, pre = 0;
		HashMap<Integer, Integer> map = new HashMap<>();
		map.put(0,1);//对于一开始的情况，下标 0 之前没有元素，可以认为前缀和为 0，个数为 1 个
		for(int i = 0; i < nums.length; i++){
			pre += nums[i];//计算前缀和
			if(map.containsKey(pre - k)){
				count += map.get(pre - k);
			}
			map.put(pre, map.getOrDefault(pre,0) + 1);
		}
		return count;
	}
}