排序

最好情况下：

冒泡排序

最坏时间复杂度 $O(n^2)$。

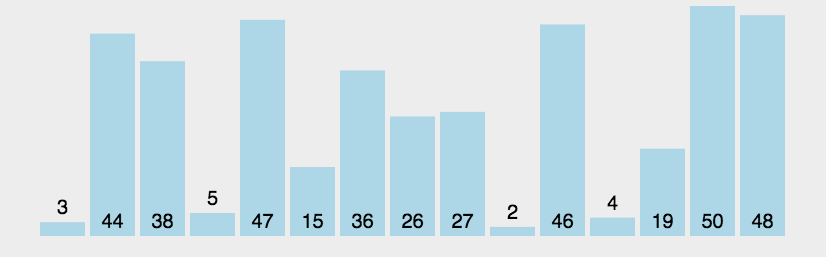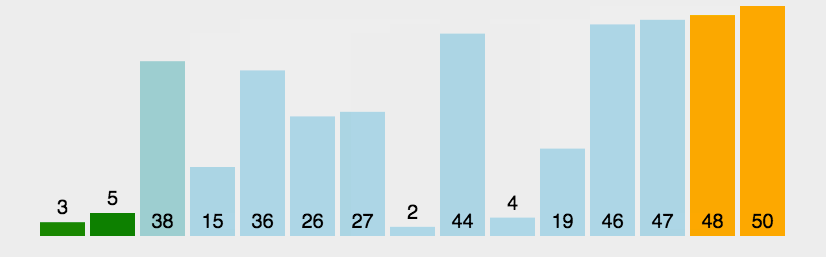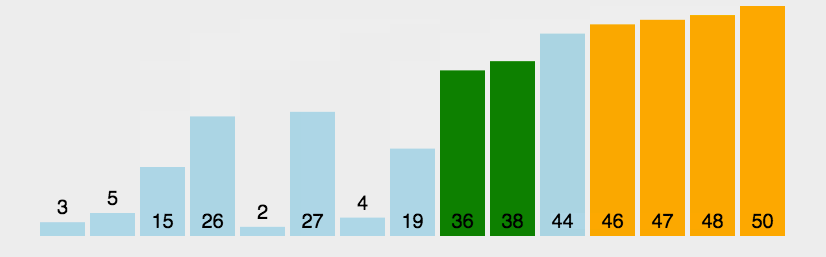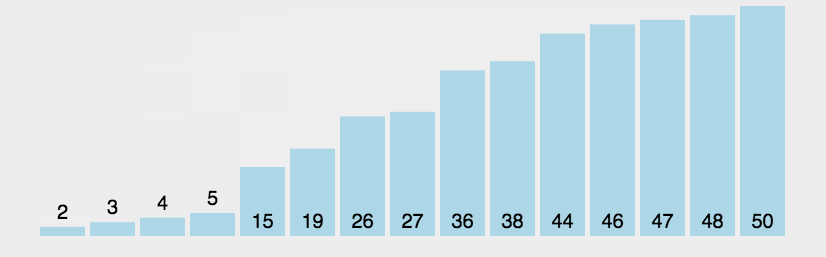
插入排序

最坏时间复杂度为 $O(n^2)$，最优时间复杂度为 $O(n)$。

平均情况下：

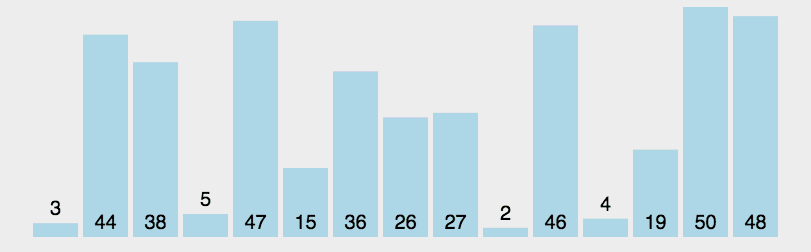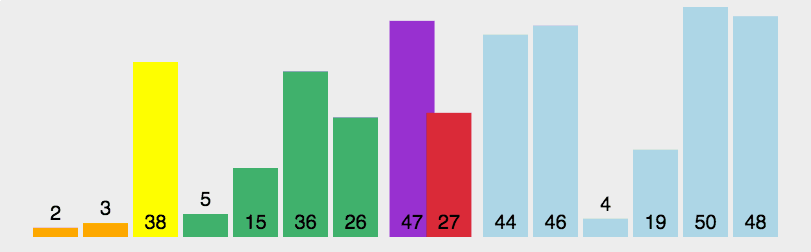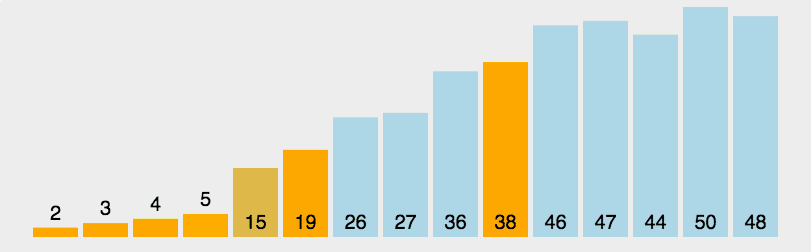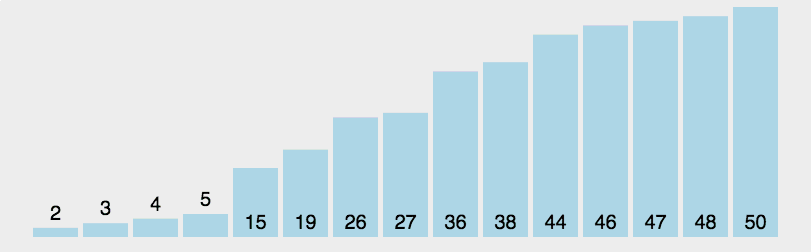
快速排序

最坏时间复杂度为 $O(n^2)$，最好时间复杂度为 $O(n\log n)$。

最坏情况下：

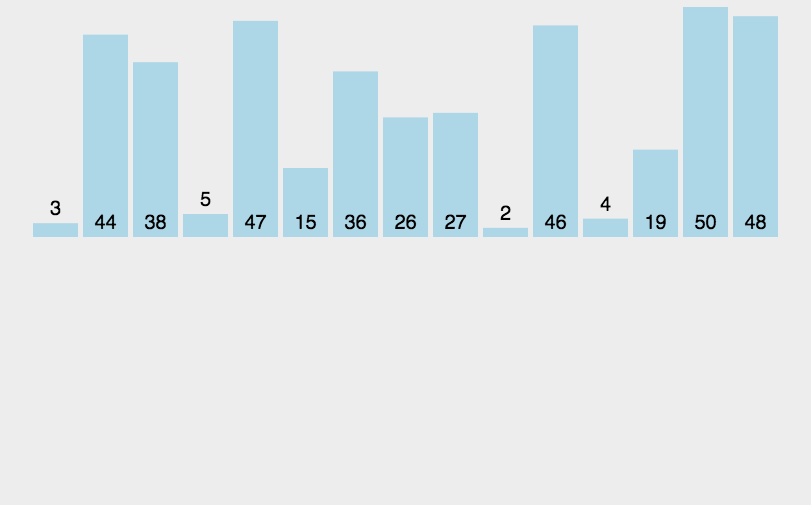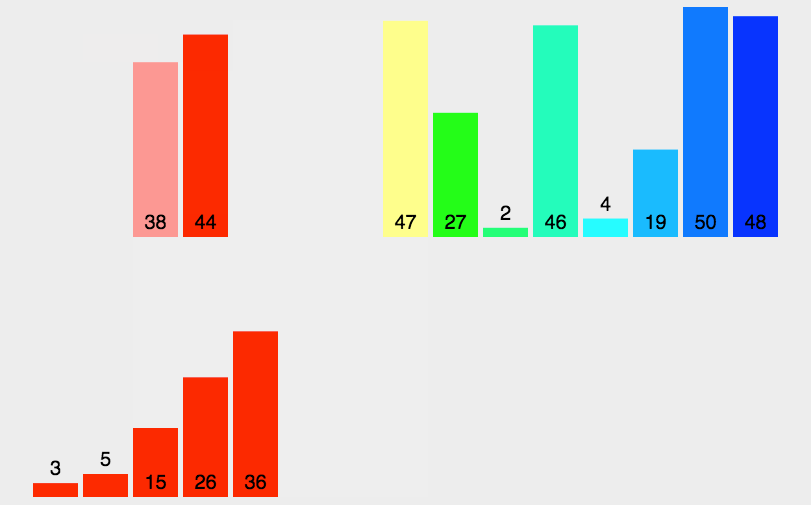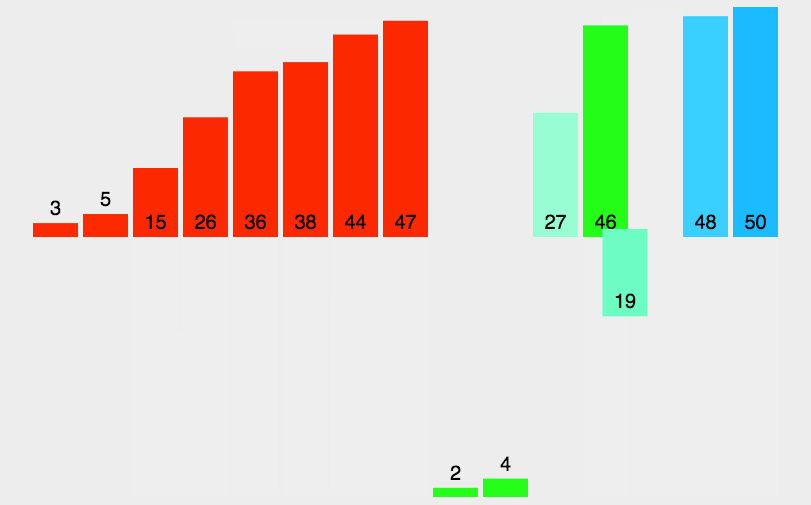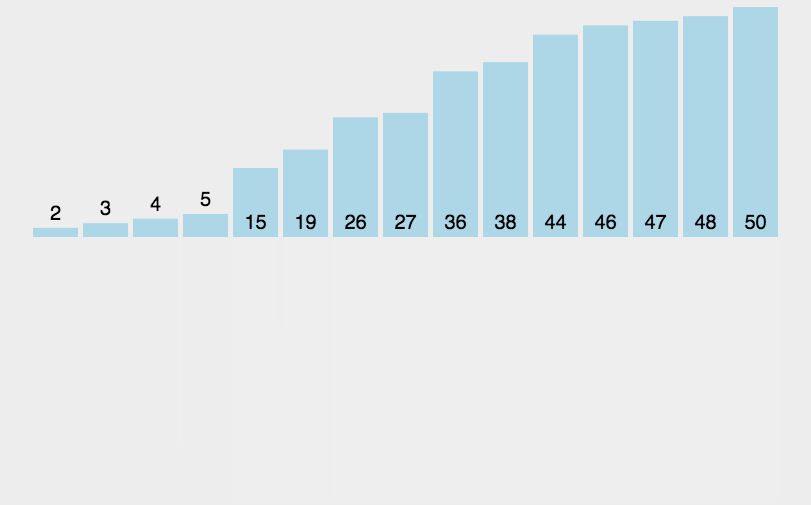
归并排序

时间复杂度稳定为 $O(n\log n)$。

---

upd on 2023/2/19：

基数排序

基数排序，是桶排序的扩展。它的基本思想是，把整数按位切割，从低位到高位排序。

具体实现就是将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后从最低位开始，依次进行一次排序。从最低位排序到最高位排序完成以后，数列就变成一个有序序列。

贪心

简介

贪心算法是从问题的初始状态出发，通过若干次的贪心选择而得到的最优值（或较优值）。

贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，至于当前状态有关。

适用前提是，局部最优策略能导致全局最优策略。

基本思路

1. 描述问题
2. 分解问题
3. 求解子问题，得到局部最优解
4. 合并子问题最优解

简单贪心问题

最优装载问题

$n$ 个物体，第 $i$ 个物体重量为 $w_i$，选择尽量多的物体，使得总重量不超过 $S$。

贪心策略：先装最轻的。

部分背包问题

$n$ 个物体，第 $i$ 个物体重量为 $w_i$，价值为 $v_i$，选择物体，每一个物体可以只取走一部分，使得总重量不超过 $S$ 且总价值尽量高。

贪心策略：先选出性价比高的。

乘船问题

$n$ 个人，第 $i$ 个人重量为 $w_i$，每艘船载重量为 $C$，最多可乘两人。用最少的船装载所有人。

贪心策略：最轻的人和最重的人配对。

常见应用

选择不相交区间问题

练手板子题

区间选点问题

练手板子题

将区间按照右端点的先后顺序排序，依次取每个区间的右端点（因为右端点可以覆盖尽量多的线段），递归操作即可。

区间覆盖问题

给 $n$ 个闭区间 $[a_i,b_i]$，选择尽量少的区间覆盖一条指定的线段区间 $[s,t]$。

练手板子题

将所有区间的左端点从大到小排序，每次选择覆盖点 $s$ 的区间中右端点坐标最大的一个，并将 $s$ 更新为该区间的右端点坐标，直到选择的区间包含 $t$ 为止。

流水作业调度问题

练手板子题1

#include<bits/stdc++.h>
using namespace std;
#define int long long

struct node
{
	int x,y,id; 
}a[1005];

int n,m,k,ans,sum; 

bool cmp(node xx,node yy)
{
	return xx.x+max(xx.y,yy.x)+yy.y<yy.x+max(yy.y,xx.x)+xx.y; 
}

signed main()
{
	cin>>n; 
	for(int i=1;i<=n;++i) cin>>a[i].x; 
	for(int i=1;i<=n;++i) cin>>a[i].y; 
	for(int i=1;i<=n;++i) a[i].id=i; 
	sort(a+1,a+n+1,cmp); 
	for(int i=1;i<=n;++i) 
		sum+=a[i].x,ans=max(sum,ans)+a[i].y; 
	cout<<ans<<endl;
	for(int i=1;i<=n;++i) cout<<a[i].id<<endl; 
	return 0; 
}

练手板子题2

和乘船问题类似，大配小即可。

#include <bits/stdc++.h>
using namespace std;

const int maxn=1005;
int N,M1,M2,ans[maxn];

struct node
{
	int id,t;
	friend bool operator < (node a,node b)
	{
		return a.t>b.t;
	}
}mach[maxn];

priority_queue<node> q1;
priority_queue<node> q2;

int main()
{
	cin>>N>>M1>>M2;
	int tmp;
	for(int i=1;i<=M1;i++) cin>>tmp,q1.push({tmp,tmp});
	for(int i=1;i<=M2;i++) cin>>tmp,q2.push({tmp,tmp});
	for(int i=1;i<=N;i++)
	{
		node now=q1.top();q1.pop();
		ans[i]+=now.t;
		q1.push({now.id,now.id+now.t});//把更新之后的时间压入
	}
	cout<<ans[N]<<' ';
	for(int i=N;i;i--)//注意因为建立的是小根堆，所以要倒着枚举
	{
		node now=q2.top();q2.pop();
		ans[i]+=now.t;
		q2.push({now.id,now.id+now.t});
	}
	sort(ans+1,ans+N+1);
	cout<<ans[N];
	return 0;
}

带限期和罚款的单位时间任务调度问题

练手板子题

前缀和、差分

前缀和

一维前缀和

1. 预处理 $O(n)$（s[i] 统计$a_1\sim a_i$ 的值）

   for(int i=1;i<=n;i++)
   	s[i]=s[i-1]+a[i]
   

2. 查询

   时间复杂度：$O(1)$

   对于区间 $[l,r]$ 的和，用前缀和数组表示为 $s_r-s_{l-1}$。

二维前缀和

1. 预处理 $O(mn)$

   for(int i=1;i<=m;i++)
   {
       for(int j=1;j<=n;j++)
       {
           scanf("%d",&a[i][j]);
           sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
       }
   }
   

2. 查询 $O(1)$

3. s[i][j]：第 $i$ 行 $j$ 列格左上部分所有元素的和。
   以 $(x_1,y_1)$ 为左上角，$(x_2,y_2)$ 为右下角的子矩阵的和为：$s(x_2,y_2)-s(x_1-1,y_2)-s(x_2,y_1-1)+s(x_1-1,y_1-1)$

差分

差分数组

首先给定一个原数组 $a$：$a_1,a_2,a_3,\cdots ,a_n$，然后我们构造一个数组 $b$：$b_1,b_2,b_3\cdots ,b_i$，使得 $a_i=b_1+b_2+b_3+\cdots +b_i$。
也就是说，$a$ 数组是 $b$ 数组的前缀和数组，反过来我们把 $b$ 数组叫做 $a$ 数组的差分数组。换句话说，每一个 $a_i$ 都是 $b$ 数组中从头开始的一段区间和。

差分

1. 一维差分、

   给 $a$ 数组中的 $[l,r]$ 区间中的每一个数都加上 $c$，只需对差分数组 $b$ 做 b[l]+=c,b[r+1]-=c 。时间复杂度为 $O(1)$。

2. 二维差分

   s[x1][y1]+=c,
   s[x2+1][y1]-=c,
   s[x1][y2+1]-=c,
   s[x2+1][y2+1]+=c;
   

倍增

倍增，顾名思义就是成倍增长，主要是在进行递推时，如果状态空间很大，通常的线性做法无法满足时间与空间复杂度的要求，可以通过成倍增长的方式，递推状态空间中在$2$的整数次幂位置上的值作为代表。当需要其他位置上的值时，通过“任意整数可以表示成若干个 $2$ 的次幂项的和”这一性质，使用之前求出的代表值拼成所需的值。

“倍增”与“二进制划分”思想结合，降低了很多问题的时间与空间复杂度。

应用：

• 快速幂
• RMQ
• LCA

递归

卡特兰数

卡特兰数，又称卡塔兰数（Catalan Number），是组合数学中一个常用的数列。其前几项为：$\boxed{1,2,5,14,42,132,429,1430,4862,\cdots }$

关于这个数列，显然我们是找不出什么规律的，所以直接把公式送给大家QwQ：

• 递归公式 $1$：
  $$f(n)=\sum _{i=0}^{n-1}f(i)\times f(n-i-1)$$

• 递归公式 $2$：
  $$f(n)=\frac{f(n-1)\times (4\times n-2)}{n+1}$$

卡特兰数的组合数学公式，详见组合数学全家桶。

汉诺塔问题

汉诺塔问题，标准递归问题。

#include <bits/stdc++.h>
using namespace std;

int k=0,n;

void mov(int n,char a,char b,char c)
{
	if(n==0)
		return;
	mov(n-1,a,b,c);
	k++;
	cout<<k<<":from "<<a<<"-->"<<c<<endl;
	mov(n-1,a,c,b);
}

int main()
{
	cout<<"n=";
	cin>>n;
	mov(n,'a','b','c');
	return 0;
}

函数：把 $n$ 片从 $a$ 柱移到 $c$ 柱的函数 mov(n,a,c,b)。

1. 先调用函数 mov(n-1,a,b,c)，把 $n-1$ 片从 $a$ 柱移到 $b$ 柱，$c$ 柱作为过渡柱。

2. 直接执行

   把 $a$ 柱上剩下的一片直接移到 $c$ 上。

   cout<<k<<":from "<<a<<"-->"<<c<<endl;
   

3. 调用 mov(n-1,b,c,a)，把 $b$ 柱上的 $n-1$ 片从 $b$ 移到 $c$ 柱上，$a$ 柱是过渡柱。

4. 直到减少到 $n=0$ 就退出。