为什么计算机要使用二进制

基数

基数：R进制每位最多使用到的不同符号的个数，R进制的基数为R。

R进制

R进制：R进制就是采用R个基本符号(0，1，2，....R-1)来表示数字的进行表示方式,R进制遵守“逢R进一”的运算规则，生活中常用的R进制又可细分为以下几类：
1.二进制
2.十进制
3.八进制
4.十六进制

二进制

二进制：由两个基本符号组成(0,1)的一种进制表示方式，遵守"逢2进一"的运算规则，后缀以B(Binary)进行表示。

例如：
(1)11110101.01B
(2)101001B

十进制

十进制：由10个基本符号组成(0,1，2，3，4，5，6，7，8，9)的一种进制表示方式，遵守"逢十进一"的运算规则，后缀以D(Decimal)进行表示

例如：
(1)145D
(2)10.35D

八进制

八进制：由8个基本符号组成(0,1，2，3，4，5，6，7)的一种进制表示方式## 标题，遵守"逢八进一"的运算规则，后缀以O(Octal)进行表示

例如：
(1)76
(2)45.4

十六进制

十六进制：由16个基本符号组成(0,1，2，3，4，5，6，7，8，9，A,B,C,D,E,F)的一种进制表示方式，遵守"逢十六进一"的运算规则，后缀以H(Hexadecimal)进行表示，也可以使用0x作为前缀来表示。

例如：

(1)A7
(2)A7.BE

R进制转十进制

R进制转十进制：任意R进制如果想要转换成十进制，只需要将每一位按权展开即可：

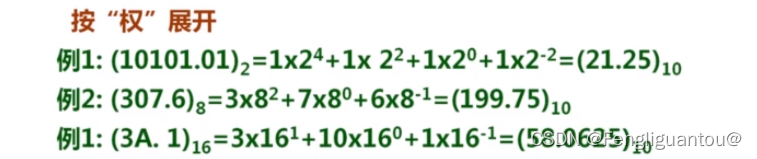
例如：八进制：77.6对应十进制： $6\times 8^{-1}+7\times 8^0+7\times 8^1=0.75+7+56=63.75$
十六进制：A6.E对应十进制：$14\times 16^{-1}+6\times 16^0+10\times 16^1=0.875+6+160=166.875$

R进制转十进制

R进制转十进制有两种方法：

  $(1)$拼凑法
拼凑法：根据十进制来反推R进制对应权值的数字。

例如：
1.十进制转二进制

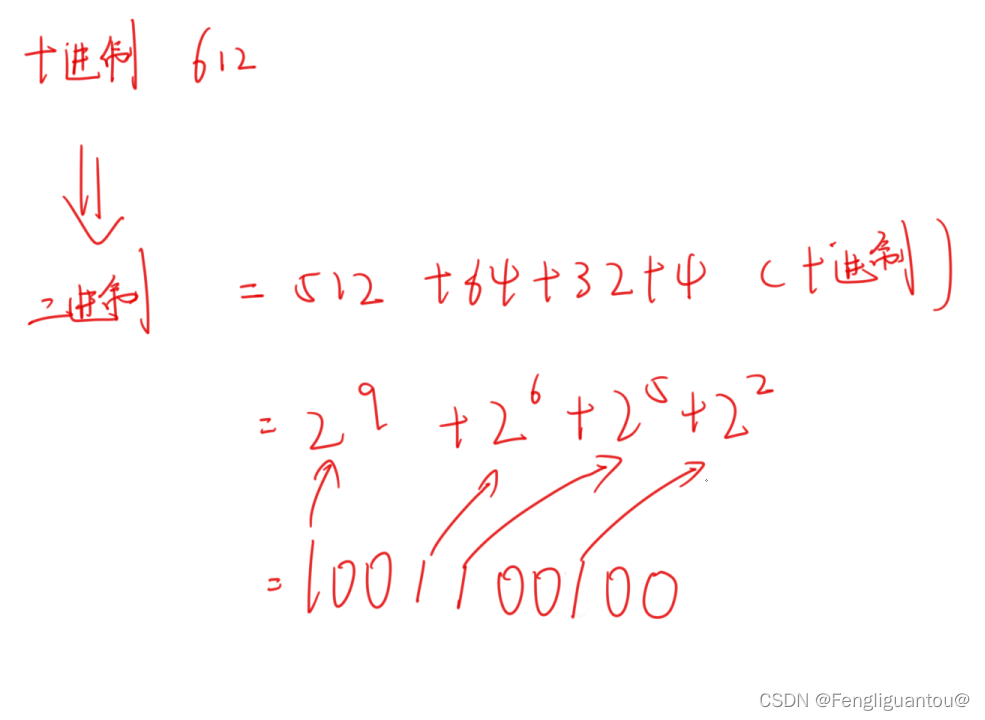
为什么能用这种拼凑的方法来进行转换呢？也就是说是一个十进制数字对应R进制一定是固定的排列组合吗？举例来说1001100100(二进制)可以表示十进制的512，有没有可能有另一种组合同样表示十进制的512呢？

答案是一定是唯一的，因为任何的R进制本质都是逢R进一，也就是说任意R进制的排列组合本质都是从1开始指向无穷的，逐渐递增的，既然如此那对应的排列组合必须也是唯一的，也就是说一个排列组合对应了一个独立的数字，所以说我们使用拼凑法得到的数字也是唯一的，但是拼凑法一般用于二进制，因为二进制除了0就是1，而其他进制基本符号较多，所以难以进行拼凑，所以可以使用短除法，或者进行间接的转换(十进制先转二进制，二进制再转对应的R进制(这种方法在后面我们会介绍))

  $(2)$短除法

短除法：短除法需要对整数部分和小数部分分别进行处理。
整数部分：不断进行短除，直到分母小于除数。
小数部分：不断进行乘，直到结果无小数部分。
读取规则：整数从下往上，小数从上往下。
取整规则：向下取整
短除法的本质：通过短除的方式判断对应权值位的数字
技巧：整数部分，先写余数，再写短除。

十进制转R进制的整数部分一定能表示出来吗？可以的， 两者本质都从0开始，每次递增1的数字。

1.十进制转二进制
其中对于整数部分的原理非常好解释，既然除2

如何理解短除法中整数部分和小数部分的处理？

1.整数部分

2.十进制转八进制

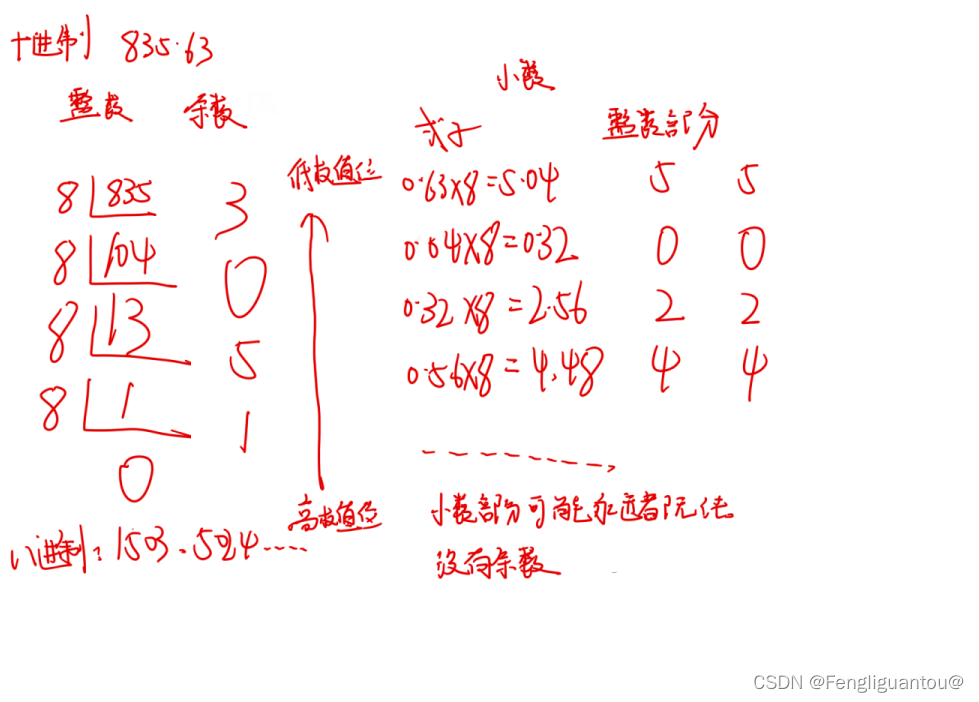
小树部分，每次乘上进制以后，若该位有数字，那么得到的结果一定是大于等于1的，并且进行下一轮乘R的时候，去掉这位对后面的位不会造成影响。

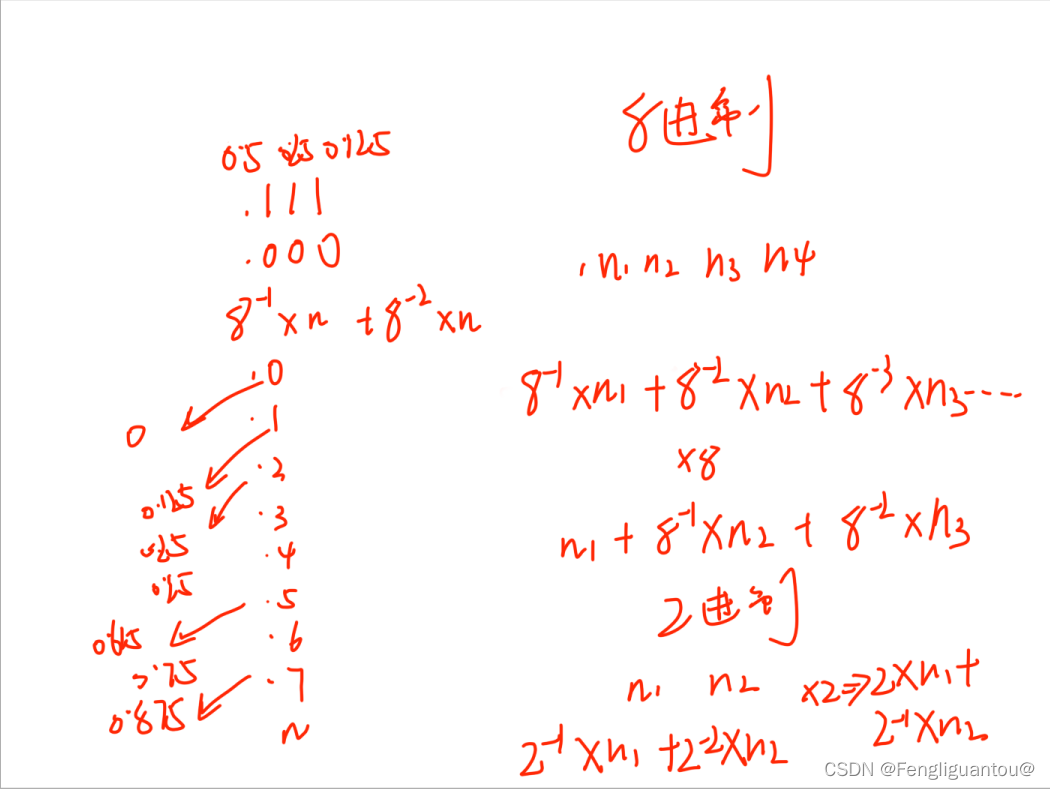
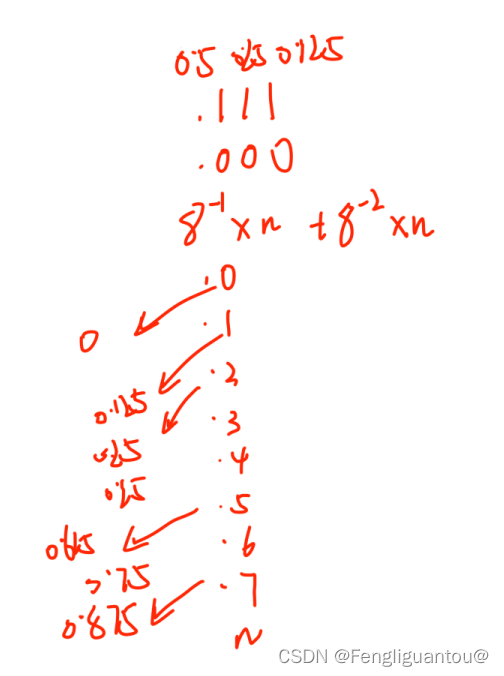
二，八，十六进制数的相互转换

  $(1)$八进制转二进制

方法：八进制的基本符号为8，二进制的基本符号为2，一个八进制位对应三个二进制位，所以只需要将八进制按照等值的二进制进行展开即可。

$(0{)}_8=(000{)}_2$
$(1{)}_8=(001{)}_2$
$(2{)}_8=(010{)}_2$
$(3{)}_8=(011{)}_2$

注：八进制转换成二进制以后，整数部分最高位，小数部分最低位的0可以去掉。

练习一：将$(13.724{)}_8$转换成二进制数。

$13.724O=$ $001011.111010100B=1011.1110101B$

练习二：将$(0.11{)}_8$转换成二进制数
$0.11O=0.001001B$

练习三：将$(0.18{)}_8$转换成二进制数
$0.18O=0.001111B$

注意：在这块一定不要和十进制混在一起了，就记住，即使是八进制小数部分同样也是按照等值的三位二进制进行转换。

  $(2)$二进制转八进制
方法：整数部分从低位向高位方向每三位用一个等值八进制来替换，最后不足三位时高位补0凑满三位，小数部分从高位向低位
方向每三位用一个等值八进制来替换，最后不足三位时低位补0凑满三位。

练习一：将$(10011.01{)}_2$转换成八进制

$10011.01B=010011.010B=23.2O$

练习一：将$(0.10101{)}_2$转换成八进制

$0.10101B=0.101010B=0.52O$

  $(3)$十六进制转二进制
十六进制和八进制转二进制的唯一区别是十六进制是四个二进制位对应一个十六进制位。

练习：将$(2B.5E{)}_{16}$转换成二进制数。

$0X2B.5E=00101011.01011110B=101011.010111B$

  $(4)$二进制转十六进制
方法：整数部分从低位向高位方向每四位用一个等值十六进制来替换，最后不足四位时高位补0凑满四位，小数部分从高位向低位
方向每四位用一个等值十六进制来替换，最后不足四位时低位补0凑满四位。

练习：将$(11001.11{)}_2$转化成十六进制数

$11001.11B=00011001.1100B=0X19.C$

注：十六进制和八进制转二进制，最后看下整数部分最高位和小数部分最低位是否有0需要去掉。

进制转换关系

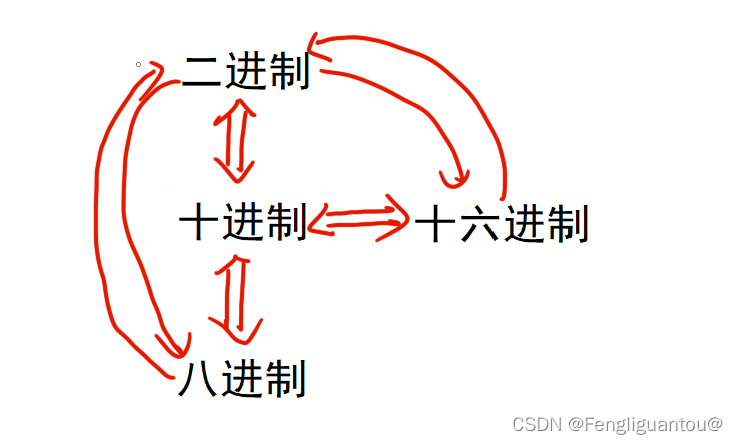
总结：
一：十进制和任意R进制都可以互转
二：十进制转八进制和十六进制有两种方法：
1.十进制直接转八进制/十六进制
2.十进制先转二进制，二进制再转八进制/十六进制

关于二进制和八进制之间的互相转换

二进制---->八进制
整数部分：从低权值位到高权值位 3位一转化 最高位不够补0
小数部分：从高权值位到低权值位 3位一转化 最低位不够补0

八进制—>二进制
整数部分：最高位的0可以去掉
小数部分：最低位的0可以去掉

进制的转换(精度问题)

无论是什么进制， 整数之间一定可以进行完整的相互转换。

小数比较特殊，任何R进制的小数都可以由十进制来进行转换。
十六进制，二进制，八进制之间无论是整数还是小数都是一定能够进行互相的完全转换的。因为都能够通过二进制为中介，而十进制的小数不是所有二进制都能转换，2，8，16一定能够互相转换，所以可以得出十进制小数不是所有2，8，16进制都能转换。

所以最终结论：
2，8，16十进制整数小数都能够完全转换
十进制整数和R进制整数互转不会有精度的缺失
R进制小数一定能由十进制表示，十进制小数不一定能完整表示为R进制小数。

进制大小的比较

结论：不管是什么进制，只要高位越大，则说明这个数越大。

例如：
F00
EFF
这里看上去可能会觉得EFF更大，但是实际上F00更大，F00的高位更大，EFF+1=F00，所以对比两个数字的大小只需要比高位。