动规五部曲

1. 确定dp数组以及下标的含义
2. 确定递归公式
3. dp数组如何初始化
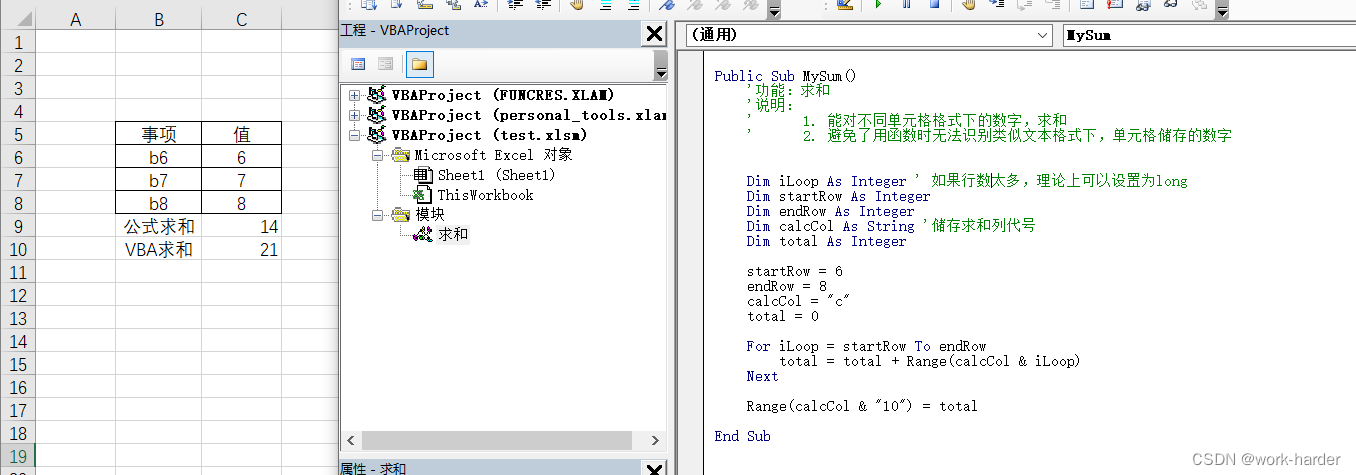
4. 确定遍历顺序
5. 举例推导dp数组

LeetCode 509. 斐波那契数

力扣题目链接

本题最直观是用递归方法

class Solution:
    def fib(self, n: int) -> int:
        if n == 0: return 0
        elif n == 1: return 1
        else:
            return self.fib(n-1) + self.fib(n-2)

当然，本题也可以用动态规划，是最简单的问题

class Solution:
    def fib(self, n: int) -> int:
        dp = [0] * (n+1)
        if n > 0:
            dp[1] = 1
        for i in range(2, n+1):
            dp[i] = dp[i-1] + dp[i-2]
        return dp[-1]

LeetCode 70. 爬楼梯

力扣题目链接
本题代码实际跟上一题斐波那契数一样。
如果是1个台阶，只有一种方法，如果有两个台阶也只有两种方法，这就是动规的初始值。
当n>2时，到达第n个台阶的最后一步可以爬1个台阶也可以爬2个台阶，如果爬1个台阶，那么前面的种数就跟n-1个台阶的情况一样；如果爬2个台阶，那么跟n-2个台阶的情况一样。
所以n个台阶的方法=n-1个台阶的方法数+n-2个台阶的方法数。这不就是不同初始值的斐波那契数列吗！

class Solution:
    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        
        dp = [0] * n
        dp[0] = 1
        dp[1] = 2
        for i in range(2, n):
            dp[i] = dp[i-1] + dp[i-2]
        return dp[-1]

LeetCode 746. 使用最小花费爬楼梯

力扣题目链接

1. 确定dp数组以及下标的含义：到达第i个台阶的最小花费
2. 确定递归公式：dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
3. dp数组如何初始化：可以从下标为 0 或下标为 1 的台阶开始爬楼梯，意味着dp[0], dp[1]初始值都为0
4. 确定遍历顺序：从前向后遍历
5. 举例推导dp数组
   

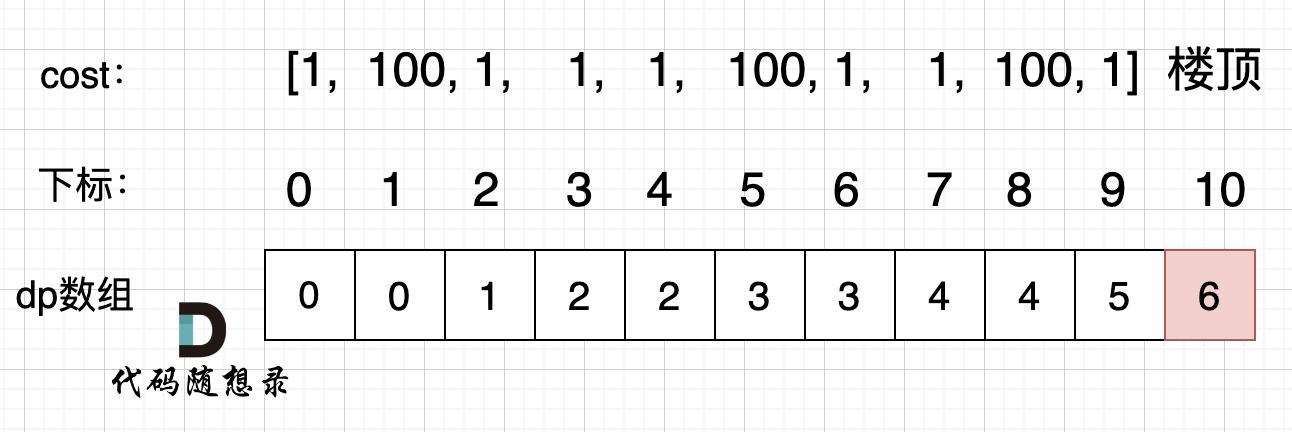
class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        dp = [0] * (len(cost) + 1)

        for i in range(2, len(cost)+1):
            dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
        return dp[-1]

今日毕！