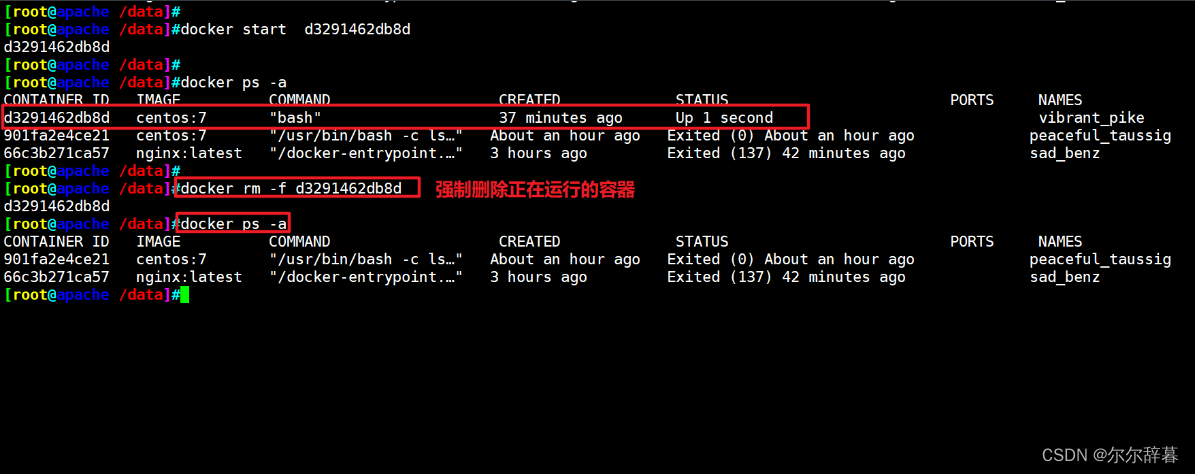
题目
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。
示例 1：

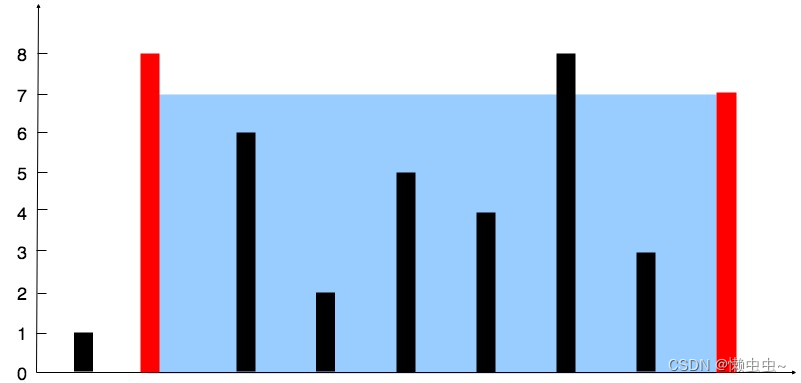
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

思路
最优的做法是使用「双指针」。双指针代表的是 可以作为容器边界的所有位置的范围。在一开始，双指针指向数组的左右边界，表示 数组中所有的位置都可以作为容器的边界，因为我们还没有进行过任何尝试。在这之后，我们每次将 对应的数字较小的那个指针 往 另一个指针 的方向移动一个位置，就表示我们认为 这个指针不可能再作为容器的边界了。

(1)求出当前双指针对应的容器的容量；
(2)对应数字较小的那个指针以后不可能作为容器的边界了，将其丢弃，并移动对应的指针。
代码

package com.it;

import java.util.Scanner;

public class Test3 {
    public static void main(String[] args) {
        // 输入任意一维数组，按照英文逗号分隔
        Scanner scanner = new Scanner(System.in);
        String str = scanner.next();
        String[] array = str.split(",");
        int[] newArray = new int[array.length];
        for (int i = 0; i < newArray.length; i++) {
            newArray[i] = Integer.parseInt(array[i]);
        }
        // 输出结果
        System.out.println(maxArea(newArray));
    }

    // 盛最多水的容器
    public static int maxArea(int[] height) {
        int left = 0;
        int right = height.length - 1;
        int ans = 0;
        while (left < right) {
            int area = Math.min(height[left], height[right]) * (right - left);
            ans = Math.max(ans, area);

            if (height[left] < height[right]) {
                ++left;
            } else {
                --right;
            }
        }
        return ans;
    }
}