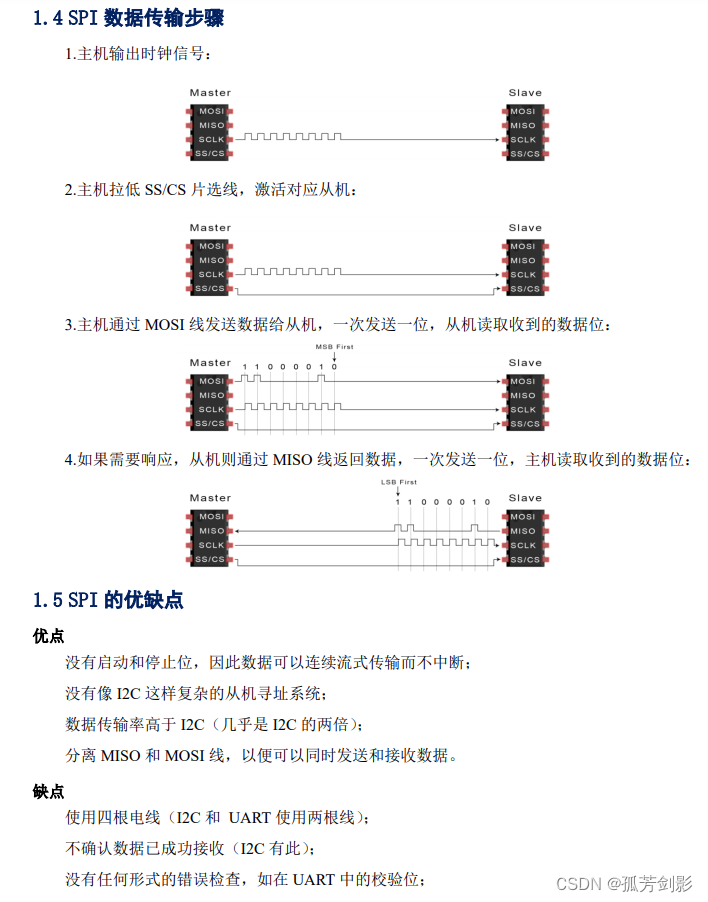
本节将介绍几大:
-
贪心搜索(greedy search)策略
-
穷举搜索(exhaustive search)
-
束搜索(beam search)
9.8.1 贪心搜索
贪心搜索已用于上一节的序列预测。对于输出序列的每一时间步 t ′ t' t′,都从 Y \boldsymbol{Y} Y 中找到具有最高条件概率的词元,即:
y t ′ = arg max y ∈ Y P ( y ∣ y 1 , … , y t − 1 , c ) y_{t'}=\mathop{\arg\max}\limits_{y\in\boldsymbol{Y}}{P(y|y_1,\dots,y_{t-1},\boldsymbol{c})} yt′=y∈YargmaxP(y∣y1,…,yt−1,c)
一旦输出序列包含了“<eos>”或者达到其最大长度 T ′ T' T′,则输出完成。

问题:
-
最优序列应该是最大化值的输出序列,而贪心搜索无法保证得到最优序列。
-
每次选择都会影响后续的所有结果。
9.8.2 穷举搜索
穷举搜索(exhaustive search)穷举地列举所有可能的输出序列及其条件概率,然后计算输出条件概率最高的一个。其计算量 O ( Y T ′ ) O(\boldsymbol{Y}^{T'}) O(YT′) 可能高的惊人。
9.8.3 束搜索
穷举搜索有精度优势,贪心搜索有计算成本优势,而束搜索则介于这两个极端之间。
束搜索(beam search)是贪心搜索的一个改进版本。它有一个超参数,名为束宽(beam size) k k k。在时间步 1,我们选择具有最高条件概率的 k k k 个词元。这 k k k 个词元将分别是 k k k 个候选输出序列的第一个词元。在随后的每个时间步,基于上一时间步的 k k k 个候选输出序列,继续从 k k k 个可能的选择中挑出具有最高条件概率的 k k k 个候选输出序列。
最后,选择其中条件概率乘积最高的序列作为输出序列。

练习
(1)我们可以把穷举搜索看作一种特殊的束搜索吗?为什么?
可以看作束宽拉满的束搜索。
(2)在 9.7 节的机器翻译问题中应用束搜索。束宽是如何影响预测的速度和结果的?
束搜索需要的计算更多,肯定是越宽越慢。
(3)在 8.5 节中,我们基于用户提供的前缀,通过使用语言模型来生成文本。这个例子中使用了哪种搜索策略?可以改进吗?
上束搜索。