此处是为澄清她两的区别， 

这两个事物 都用的相同的符号表示， 即这个圈数符号，

它在数学中有许多不同的含义，

本文讨论的是：“张量积”，它是对张量的运算； 以及“Kronecker ”积，它是对数组的运算。

基本总结是“张量积”将两个张量组合成一个新的第三个张量；
而“Kronecker ”积 将两个数组合成一个新的第三个数组。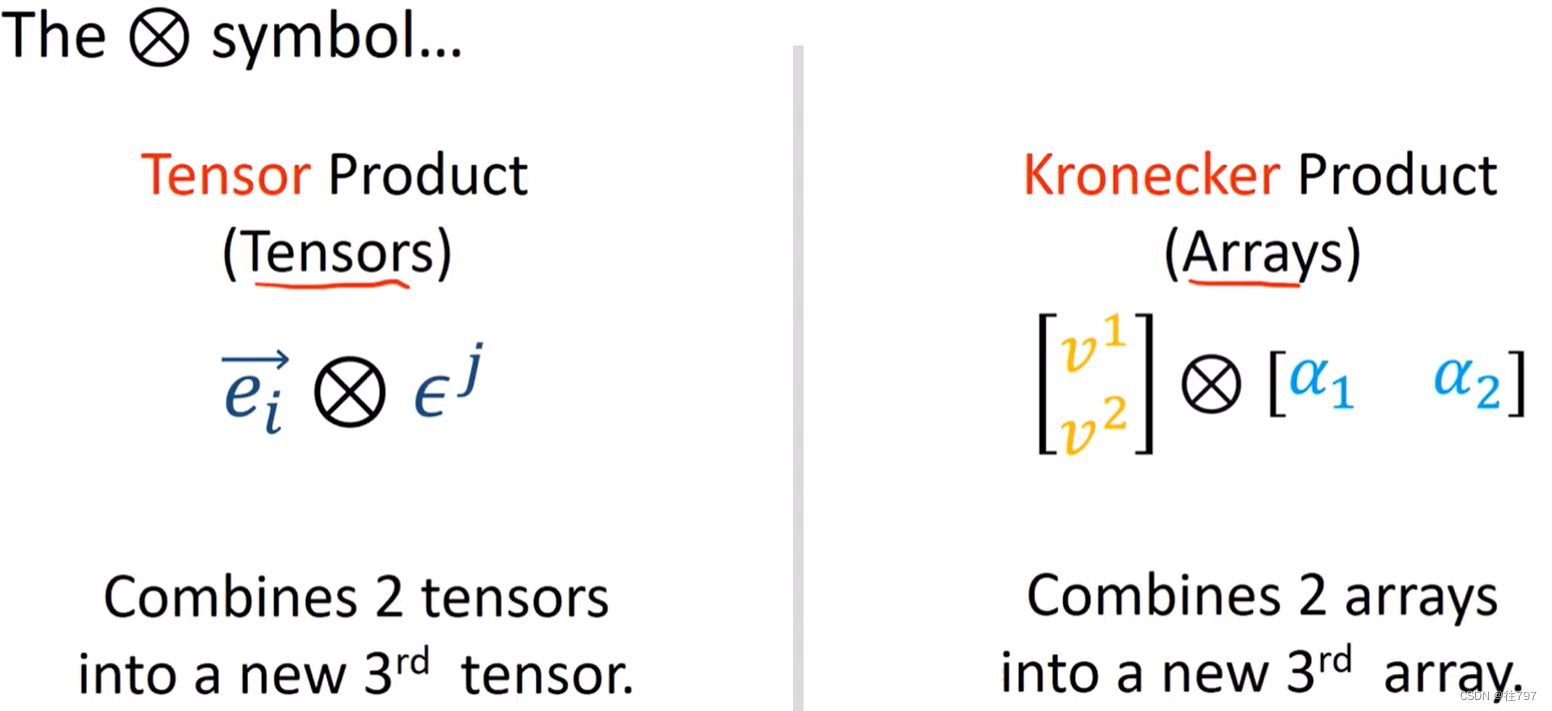

从张量积开始，

协向量是由这里的这些规则定义的线性函数，其中协向量作用在向量上，给出了Kronecker Delta作为结果。

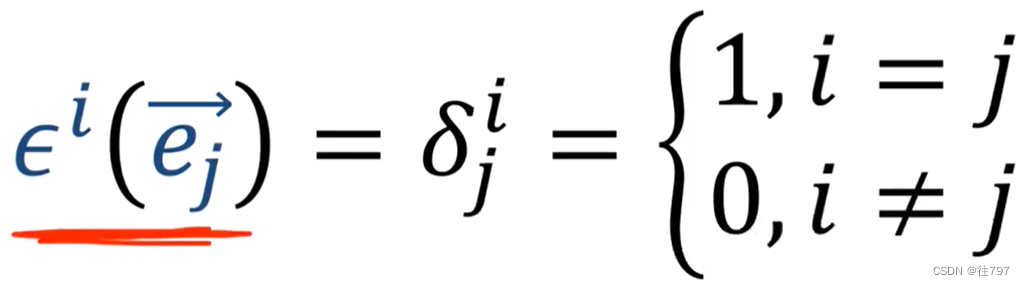
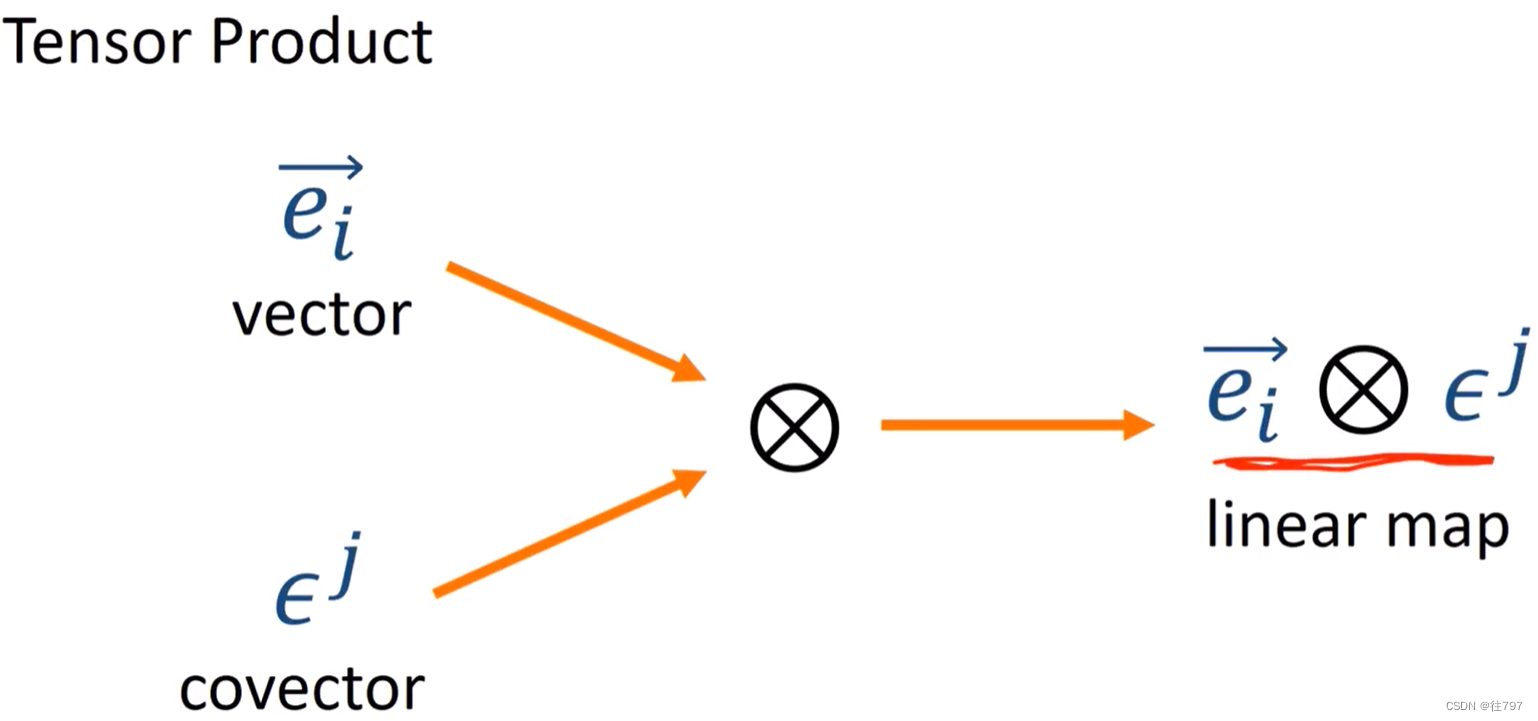
这三个都是张量。

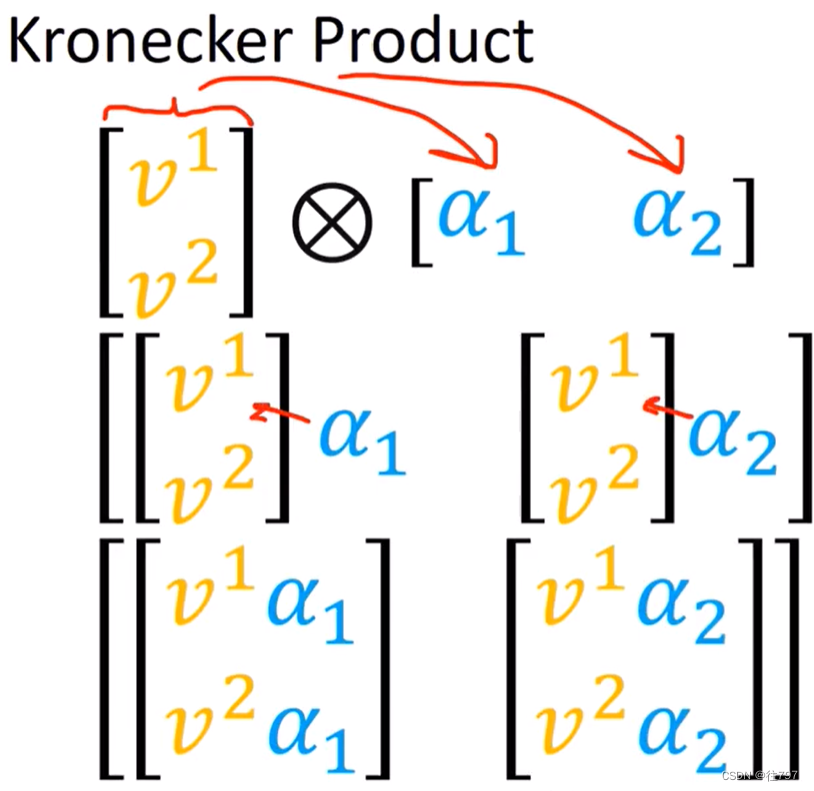
Kronecker Product

该乘积将采用这两个数组(在这种情况下恰好是一个列向量和一个行向量)，它将产生第三个数组。

因此，它通过获得左侧的第一个数组，并将其分配给右侧数组中的每个元素来实现这一点。

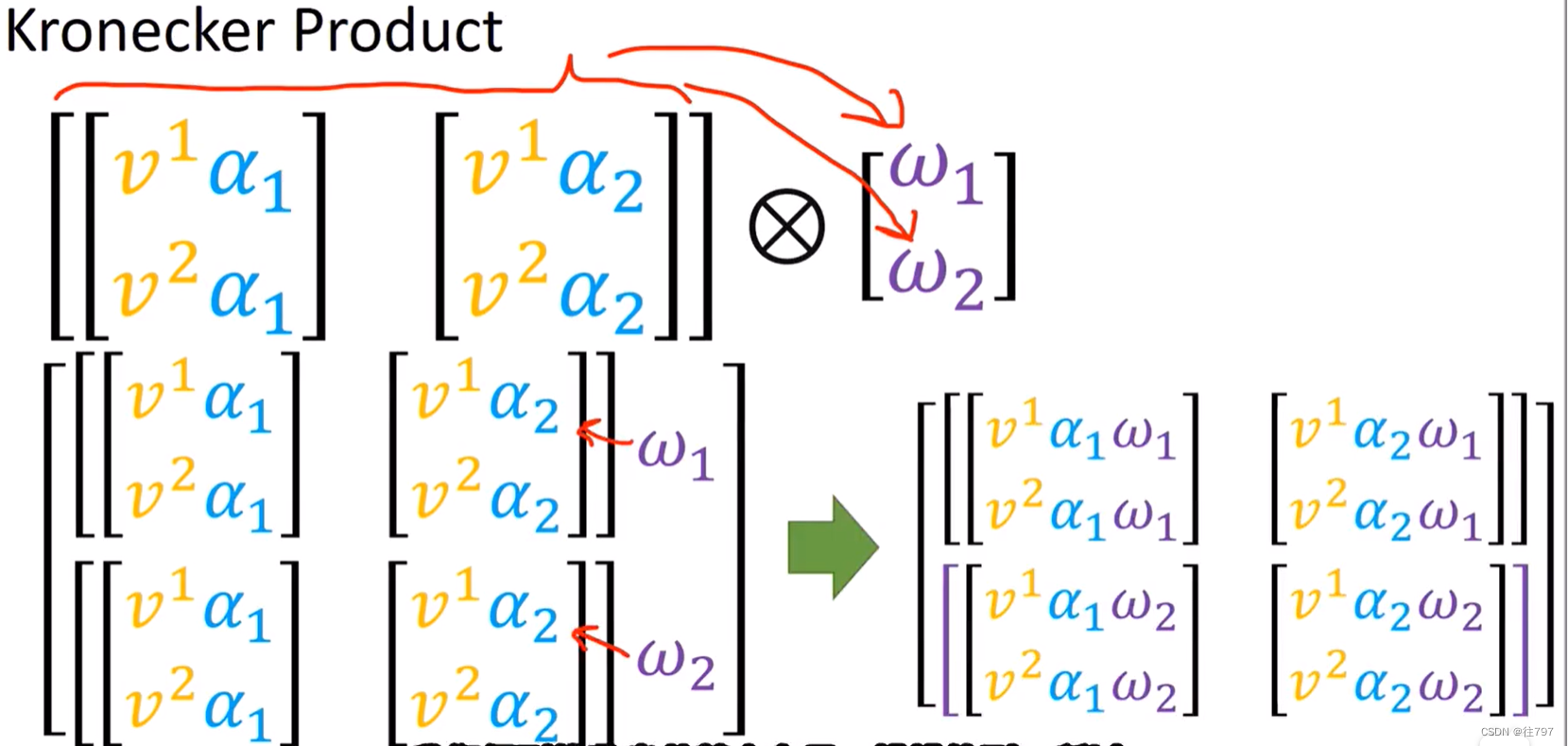
所以张量积 和 Kronecker 积 是两个不同的东西，但它们又高度相关。

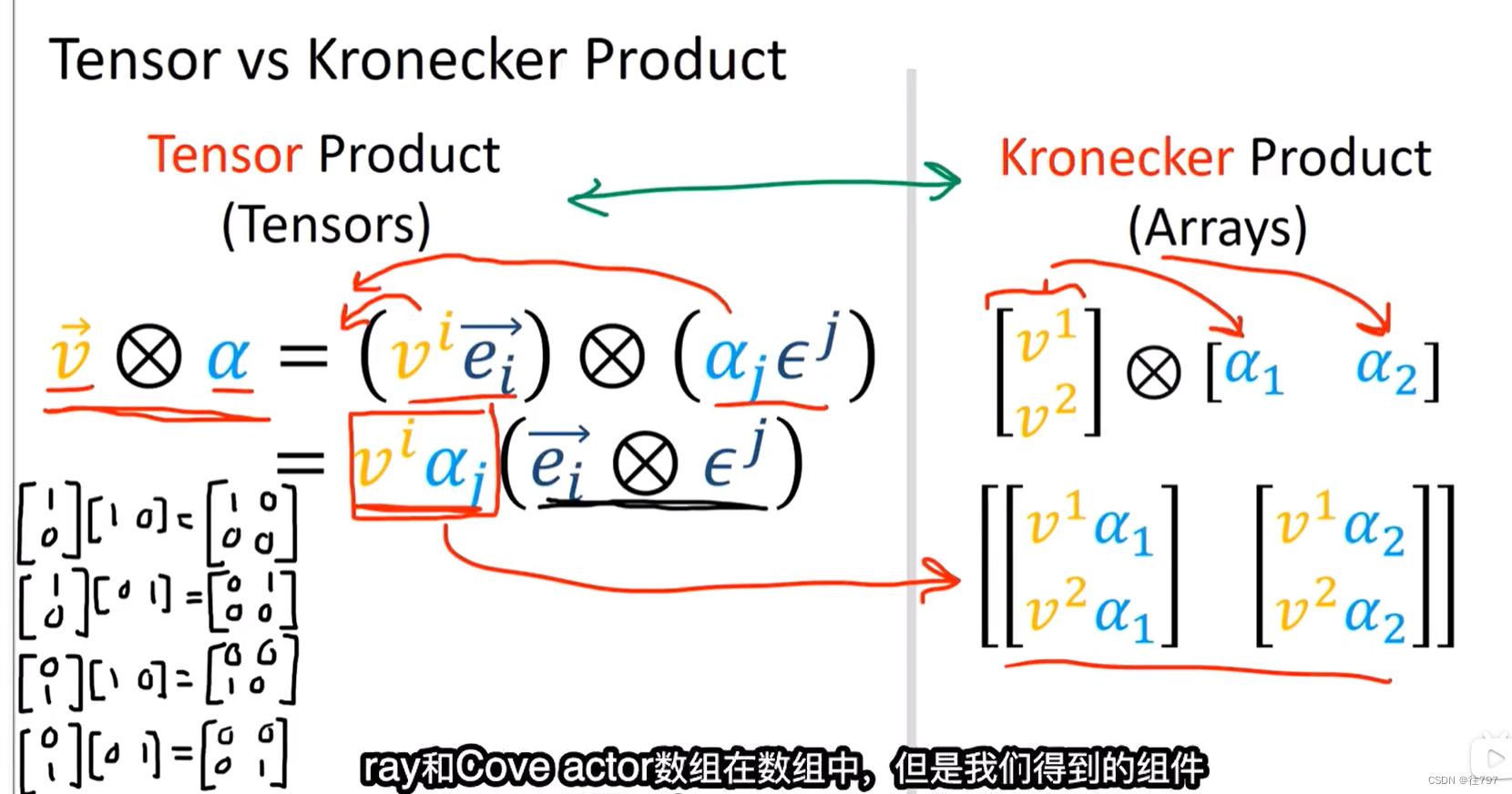
这两个积基本上是在做同样的事情，只是张量积结合了代数符号领域的抽象向量和抽象协向量，而Kroneck 积 结合了向量数组 和 数组领域中的协向量数组。

但是我们从张量积中得到的分量  只是我们从Kroneck积中得到的矩阵的分量。

所以，实际上，张量积和Kroneck积有点像同一个运算，它们只是在不同的上下文中做工作，