概率论 - 常见分布（及其分布表）

常见分布的期望和方差

离散型分布

两点分布

有2种结果，实验只做1次

X~b(1,p)则有
P(X = k) = p^k (1-p)^1-k,k = 0, 1
数学期望：E(X) = p
方差：D(X)=p(1-p)

二项分布

P(A) = p，在n次实验中，事件A发生了k次。

记作：X ~ B(n, p)
P(X = k) = C^k_n p^k(1-p)^n-k
期望：E(X) = np
方差：D(X) = np(1-p)=npq

最可能值：
（1）当（n+1）p不为整数时，二项概率P{X=k}在k=[(n+1)p]时达到最大值；
（2）当（n+1）p为整数时，二项概率P{X=k}在k=(n+1)p和k=(n+1)p-1时达到最大值。
注：[x]为不超过x的最大整数。

若满足二项分布X ~ B(n, p)，其中n足够大（n≥100），且 np≤10 时。
可以将其近似于泊松分布 X ~ P(np)【λ = np】，然后在查表就可以了。

泊松分布

泊松分布适合于描述单位时间（或空间）内随机事件发生的次数。
记作：X ~ P(λ)

EX = DX = λ

几何分布

实验E只有两个可能的结果A和A的对立事件B，P(A) = p, P(B) = 1 - p(0<p<1),把实验E重复独立地进行下去，直到事件A首次发生，所需要的试验次数X（1，2，3……）
X~Ge( p)
P(x = k) = (1-p)^k-1p, k = 1, 2,3……
EX= 1/p
DX = q / p²

超几何分布

共有N件产品，其中有M件次品。从中任取n件，次品数量为x

X ~ H(n,M,N)

随机型

均匀分布

一个均匀分布在区间[a, b]上的连续型随机变量X可给出如下概率密度函数：

X~U(a, b)
EX = (a + b) / 2
DX = (b-a)²/12

指数分布（寿命分布）

某一特定事件发生所需等待时间。
概率密度函数：

X~E(λ)
EX = 1 / λ
DX = 1 / λ²

正态分布（高斯分布）

两头小中间大，左右还对称


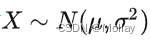
EX= μ
DX= σ²