5.7 约束优化最优性理论应用实例

5.7.1 仿射空间的投影问题

考虑优化问题
$$\begin{gathered} \underset{x\in R^n}{\min }\frac{1}{2}||x-y|{|}_2^2, \\ s.t.Ax=b \end{gathered}$$
其中$A\in R^{m\times n},b\in R^m,y\in R^n$为给定的矩阵和向量，这里不妨设矩阵A是行满秩的，这个问题可以看成仿射平面 { x ∈ R n ∣ A x = b } \{x{\in}R^n|Ax=b\} {x∈Rn∣Ax=b}的投影问题
对于等式约束，我们引入拉格朗日乘子$\lambda \in R^m$，构造拉格朗日函数
$$L(x,\lambda )=\frac{1}{2}||x-y|{|}^2+{\lambda }^T(Ax-b)$$
因为只有仿射约束，估$Slater$条件满足，$x^{\ast }$为一个全局最优解，当且仅当存在${\lambda }^{\ast }\in R^m$使得
$$\{\begin{array}{c}{x}^{\ast }-y+A^T\lambda =0\\ A{x}^{\ast }=b\end{array}$$
由上述KKT条件第一式，等号左右两边同时左乘$A$可得
$$A{x}^{\ast }-Ay+A{A}^T\lambda =0$$
注意到$A{x}^{\ast }=b$以及$A{A}^T$是可逆矩阵，因此可以解出乘子
$$\lambda =(A{A}^T{)}^{-1}(Ay-b)$$
代入回去可以得到
$$x^{\ast }=y-A^T(A{A}^T{)}^{-1}(Ay-b)$$

5.7.2 线性规划问题

考虑线性规划问题
$$\begin{gathered} \underset{x\in R^n}{\min }{c}^{T}x, \\ s.t.Ax=b, \\ x\ge 0\text{\hspace{1em}(5.7.1)} \end{gathered}$$
其中$A\in R^{m\times n},b\in R^m,c\in R^n$分别为给定的矩阵和向量
拉格朗日函数可以写为
$$\begin{gathered} L(x,s,v)=c^{T}x+v^T(Ax-b)-s^{T}x \\ =-b^{T}v+(A^{T}v-s+c{)}^{T}x,s\ge 0 \end{gathered}$$
其中$s\in R^n,v\in R^m$，由于线性规划是凸问题且满足$Slater$条件的，因此对于任意一个全局最优解$x^{\ast }$，我们有如下KKT条件
$$\{\begin{array}{c}c+A^T{v}^{\ast }-s^{\ast }=0,\\ A{x}^{\ast }=b\\ x^{\ast }\ge 0\\ s^{\ast }\ge 0\\ s^{\ast }{x}^{\ast }=0\end{array}\text{\hspace{1em}(5.7.2)}$$
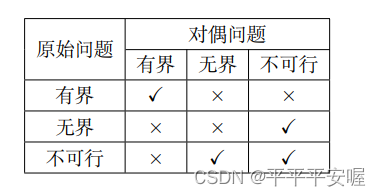
我们设原始问题和对偶问题最优解函数值分别为$p^{\ast }$和$d^{\ast }$，则根据$p^{\ast }$取值情况，有如下三种可能
（1）如果$-\infty <p^{\ast }<+\infty (有界)$，那么原始问题可行而且存在最优解，由$Slater$条件知强对偶原理成立，因此有$d^{\ast }=p^{\ast }$，即对偶问题也是可行的且存在最优解
（2）如果$p^{\ast }=-\infty$，那么原始问题可行，但目标函数值无下界，由弱对偶原理知$d^{\ast }\le p^{\ast }=-\infty$，即$d^{\ast }=-\infty$，因为对偶问题是对目标函数极大化，所以此时对偶问题不可行
（3）如果$p^{\ast }=+\infty$，那么原始问题无可行解，注意到$Slater$条件对原始问题不成立，此时对偶问题既可能是函数值无界（$d^{\ast }=+\infty$）也可能无可行解（$d^{\ast }=-\infty$），我们说，不可能出现$-\infty <d^{\ast }<+\infty$的情形，这是因为如果对偶问题可行且存在最优解，那么可对对偶问题应用强对偶原理，进而导出原始问题也存在最优解，这矛盾了

5.7.3 基追踪

$$\begin{gathered} \underset{x\in R^n}{\min }||x|{|}_1, \\ s.t.Ax=b\text{\hspace{1em}(5.7.3)} \end{gathered}$$
利用分解$x_i=x_i^{+}-x_i^{-}$，其中 x i + = m a x { x i , 0 } , x i − = max ⁡ { − x i , 0 } x_i^+=max\{x_i,0\},x_i^-=\max\{-x_i,0\} xi+​=max{xi​,0},xi−​=max{−xi​,0}分别表示$x$的正部和负部，问题5.7.3的一种等价形式可以写成
$$\begin{gathered} \min \sum _i{x}_i^{+}+x_i^{-}, \\ s.t.A{x}^{+}-A{x}^{-}=b, \\ {x}^{+},x^{-}\ge 0 \end{gathered}$$
进一步的，令$y=[x_i^{+},x_i^{-}{]}^T\in R^{2n}$，我们将问题5.7.3转化为如下线性规划问题
$$\begin{gathered} \underset{y\in R^{2n}}{\min }{1}^{T}y, \\ s.t.[A,-A]y=b, \\ y\ge 0 \end{gathered}$$
其中$1=(1,1,\cdots ,1{)}^T\in R^{2n}$
那么根据一般线性规划的最优性条件，等价于求解
$$\{\begin{array}{c}1+[A,-A{]}^T{v}^{\ast }-s^{\ast }=0,\\ [A,-A]y^{\ast }=b\\ y^{\ast }\ge 0\\ s^{\ast }\ge 0\\ s^{\ast }{y}^{\ast }=0\end{array}\text{\hspace{1em}(5.7.4)}$$
同样的，我们也可以直接推导5.7.3的最优性条件，拉格朗日函数为
$$L(x,v)=||x|{|}_1+v^T(Ax-b)$$
$x^{\ast }$为全局最优解当且仅当存在$v^{\ast }\in R^m$使得
$$\{\begin{array}{c}0\in \partial ||x^{\ast }|{|}_1+A^T{v}^{\ast },\\ A{x}^{\ast }=b\end{array}\text{\hspace{1em}(5.7.5)}$$
最优性条件5.7.4和5.7.5本质上是等价的