抽象地说,解决一个回溯问题,实际上就是遍历一棵决策树的过程,树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍,把叶子节点上的答案都收集起来,就能得到所有的合法答案。站在回溯树的一个节点上,你只需要思考 3 个问题:
- 路径:也就是已经做出的选择。
- 选择列表:也就是你当前可以做的选择。
- 结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯算法的框架:
回溯算法框架代码
以下就是回溯算法的框架代码
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」
排列、组合、子集
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素,主要有以下几种变体:
- 元素无重不可复选【I】,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式。以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该只有 [7]。
- 元素可重不可复选【II】,即 nums 中的元素可以存在重复,每个元素最多只能被使用一次。以组合为例,如果输入 nums = [2,5,2,1,2],和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
- 元素无重可复选,即 nums 中的元素都是唯一的,每个元素可以被使用若干次。以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该有两种 [2,2,3] 和 [7]。
当然,也可以说有第四种形式,即元素可重可复选。但既然元素可复选,那又何必存在重复元素呢?元素去重之后就等同于形式三,所以这种情况不用考虑。
排列
排列的概念和排列树
排列的概念
全排列是一个组合数学概念,它指的是一个给定集合中所有元素的不同排列方式【不同顺序是两个】。全排列是一个重要的排列组合问题,通常用于解决诸如排列、组合、密码学和计算机算法等领域的问题。
假设有一个集合,其中包含n个不同的元素,全排列就是这些元素的所有可能的排列方式。每个元素在每个排列中都只出现一次。全排列问题通常用于计算和枚举这些排列,以便解决各种问题,如密码破解、计算机编程中的排列操作等。
在数学符号中,全排列通常用符号P(n)来表示,其中n表示集合中元素的数量。因此,对于上述例子,P(3) = 3! = 3 × 2 × 1 = 6。全排列的数量等于元素个数的阶乘。
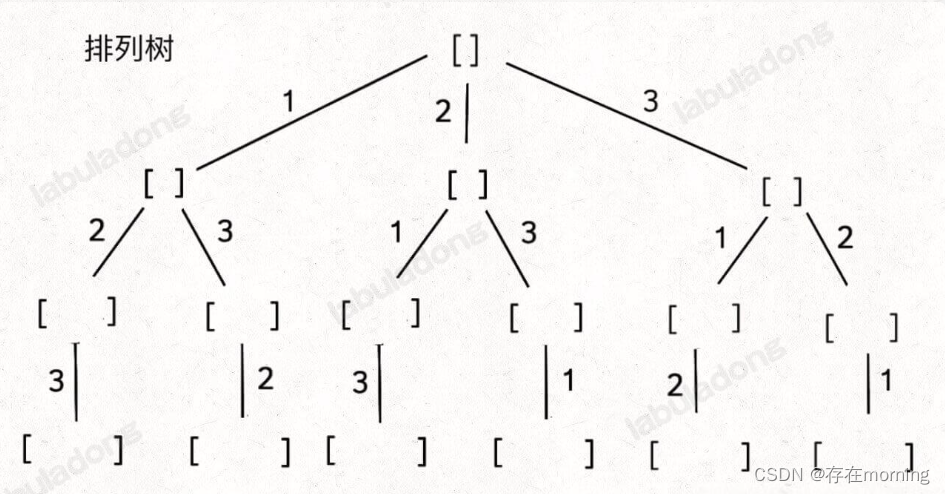
排列树
排列树如下
子集
子集的概念和子集树
子集的概念
组合问题和子集问题其实是等价的,什么是子集呢?子集是集合论中的一个重要概念,它指的是一个集合中的部分元素的集合。更具体地说,如果集合A中的所有元素都包含在集合B中,那么A是B的一个子集。这可以用符号表示为A ⊆ B。
以下是子集的一些关键特点和定义:
-
子集关系:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集
-
空集合是任何集合的子集:空集合(不包含任何元素的集合)是所有集合的子集。形式化地,∅(空集合)是任何集合A的子集,即∅ ⊆ A。
-
集合是其自身的子集:任何集合都是其自身的子集,即对于任何集合A,A ⊆ A。
-
真子集:如果A是B的子集,但A和B不相等,那么A被称为B的真子集。形式化地,如果A ⊆ B 且 A ≠ B,那么A是B的真子集,可以表示为A ⊂ B。
例如,假设有两个集合:
A = {1, 2}
B = {1, 2, 3, 4}
在这种情况下,集合A是集合B的子集,因为A中的所有元素都包含在B中。所以,A ⊆ B。同时,A也是B的真子集,因为它们不相等,即A ≠ B,可以表示为A ⊂ B。
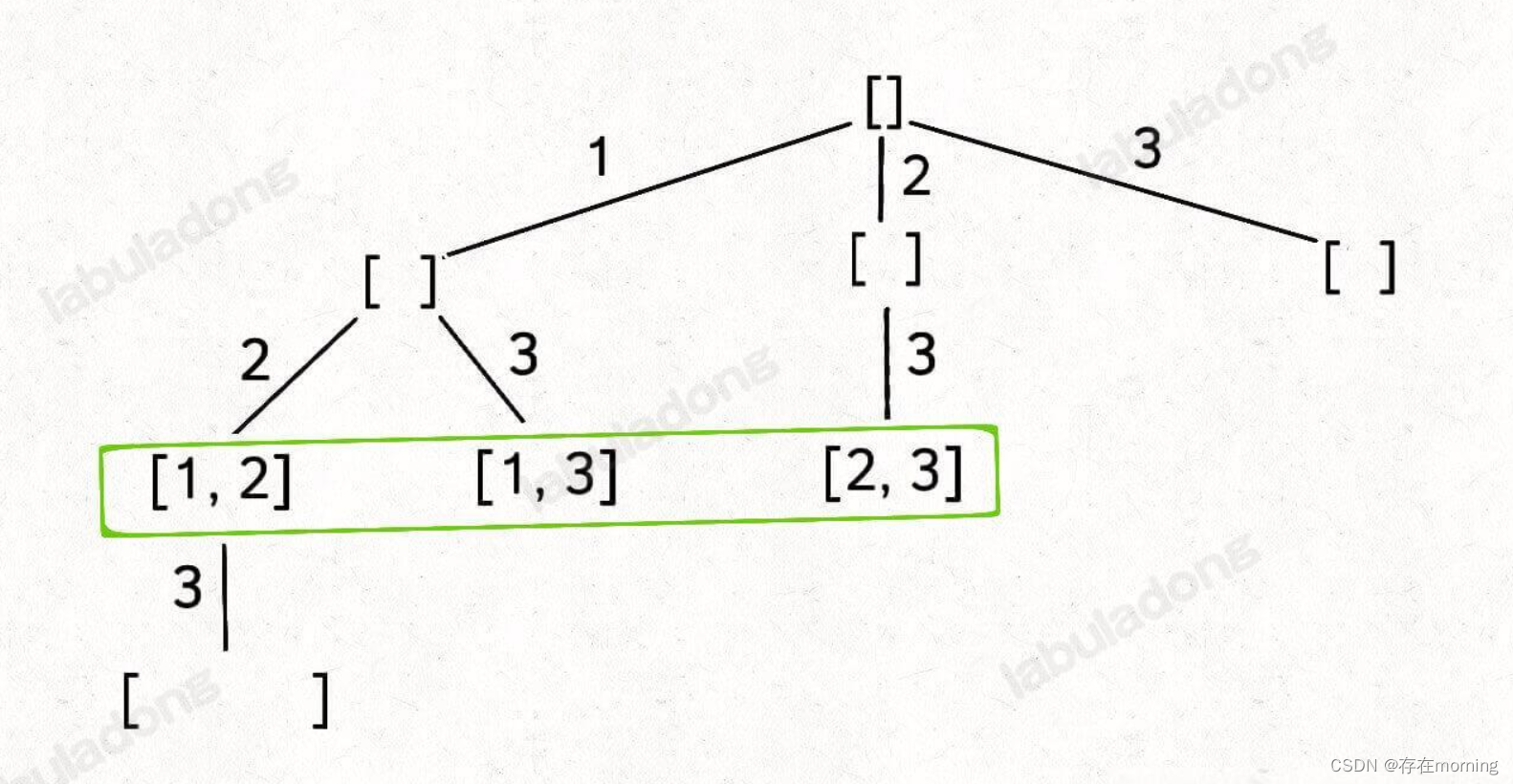
子集树
子集树如下
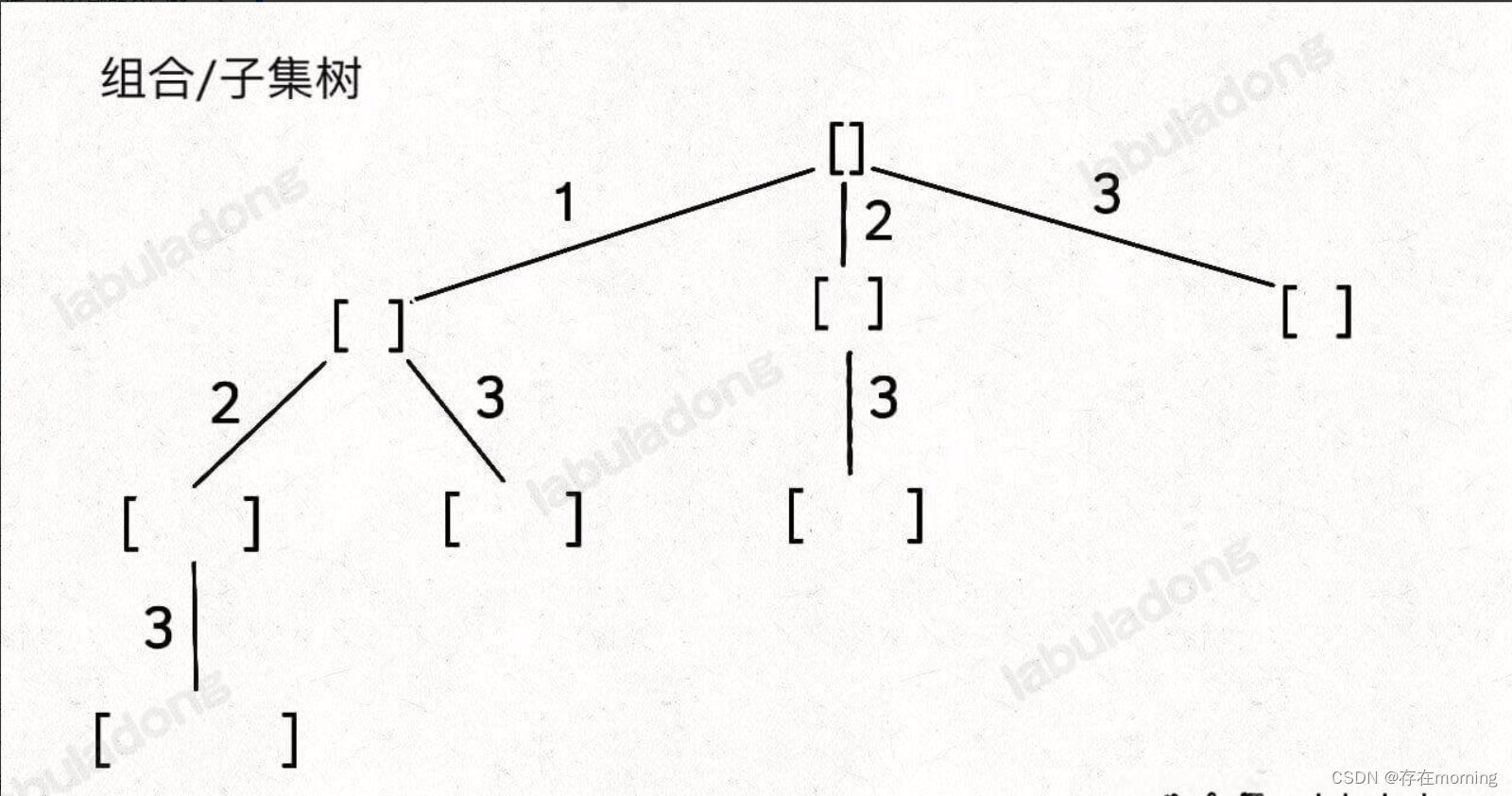
所有子集,就是把所有节点的值都收集起来
组合
组合的概念和组合树
组合的概念
组合是组合数学中的一个重要概念,它涉及从给定的集合中选择出一定数量的元素,而不考虑元素的顺序。组合用来计算在不同的选择中,选取一组元素的方式,而不考虑它们的排列顺序。组合通常表示为 “C(n, k)”,其中 “n” 表示集合中的元素数量,“k” 表示要选择的元素数量。
组合的定义如下:
在集合中,从n个不同的元素中选择k个元素,其中1 ≤ k ≤ n,这种选择方式称为一个组合。组合通常用 “C(n, k)” 表示,其中 “n” 是总元素数量, “k” 是选择的元素数量。组合的数量可以用以下公式计算:
C(n, k) = n! / (k!(n-k)!)
其中 “n!” 表示n的阶乘,即n的所有正整数的乘积。
组合与排列不同,排列考虑元素的顺序,而组合仅考虑元素的选择,无论其顺序如何。例如,如果有一个集合 {A, B, C},那么从中选择两个元素的组合有三种:{A, B}、{A, C} 和 {B, C},而不考虑元素的排列顺序。
组合的应用非常广泛,包括在组合优化、统计学、概率论、密码学、计算机科学和组合数学等领域。
组合树
组合树与子集树相同,只不过是子集树上满足条件的某一层节点
排列、子集、组合的区别和联系
下表是排列、子集和组合的联系与区别的简要总结:
| 特点 | 排列(Permutation) | 子集(Subset) | 组合(Combination) |
|---|---|---|---|
| 定义 | 考虑元素的排列顺序 | 不考虑元素的排列顺序 | 不考虑元素的排列顺序 |
| 选择元素个数(k) | k个元素 | 0到n个元素 | k个元素 |
| 顺序重要性 | 重要 | 不重要 | 不重要 |
| 表示形式 | P(n, k) | - | C(n, k) |
| 计算公式 | n! / (n-k)! | - | n! / (k!(n-k)!) |
| 例子 | 排列一组车辆的顺序 | 集合中的元素的所有可能子集 | 从一组学生中选择小组 |
这个表格总结了排列、子集和组合的定义、特点、选择元素个数、顺序重要性、表示形式和计算公式,以帮助理解它们之间的联系和区别。