1 神经网络分类问题

分类问题，通常分为二分类问题与多分类问题（大于2类）。

2 二分类问题

2.1 网络设计

神经网络的最后一层（输出层），为一个神经元，使用激活函数sigmoid。

tf.keras.layers.Dense(1,activation="sigmoid")

使用sigmoid激活函数将输出压缩到0-1的范围，其输出值为1类的概率。

2.2 损失函数

在神经网络训练过程中，若某样本的标签为1，神经网络的输出0.9（表示1类的概率为90%），尽管此时可认为输出的类别为1类（通常以0.5为边界，大于0.5为1类，小于0.5为0类）；但神经网络并没有100%确定（输出1）是1类，存在损失，需要进一步优化参数，使输出接近于1。

此时定义损失函数binary_crossentropy交叉熵损失：

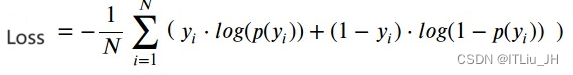
其中yi为样本真实的标签，p(yi)为模型输出值（样本为1类的概率）。

当样本真实标签为1，样本为1类的概率为1，求和项的前后均为0，损失为0；

当样本真实标签为0，样本为1类的概率为0，同样求和项的前后均为0，损失为0；

而当样本为1类或者0类，而概率不为1或0时，存在损失>0，对batch中样本的损失求平均，得到平均损失，进一步的优化网络参数。

model.compile(...,
              loss=tf.keras.metrics.binary_crossentropy,

              ...)

3 多分类问题

3.1 网络设计

神经网络的最后一层（输出层），为N个神经元（N分类问题，N>2），使用激活函数softmax。

tf.keras.layers.Dense(N,activation="softmax")

使用softmax激活函数将多输出求和，然后计算每个输出的占比（可以理解为对应类别的概率），作为模型的输出，占比最高的输出神经元的位置为模型确定的类别（np.argmax()）。

3.2 损失函数

在神经网络训练过程中，若某样本的标签为3，神经网络的输出第3神经元的输出0.5（表示3类的概率为50%，所有输出神经元的输出的最大值），尽管此时可认为输出的类别为3类（最大值所在的神经元位置）；但神经网络并没有100%确定（输出3）是3类，存在损失，需要进一步优化参数，使神经元3的输出接近于1。此时定义损失函数

其中yi为样本one-hot标签第i位的值，p(yi)为网络输出层第i个神经元的输出。由于标签one-hot编码中只有一位为1，其它为0，本质上此时交叉熵损失只关注真实标签中1对应的一个神经元的输出。

常用categorical_crossentropy和sparse_categorical_crossentropy交叉熵。

当数据集标签为1维时（如，样本类别为5时，标签为5），采用sparse_categorical_crossentropy计算损失。此时输出为N维，标签为1维。

model.compile(...,
              loss=tf.keras.metrics.sparse_categorical_crossentropy,

              ...)

当数据集标签为N维时（标签采用one-hot编码，或者tf.keras.utils.to_categorical编码。如，样本类别为5时，标签为（0，0，0，0，1，0,...）N维）。采用categorical_crossentropy计算损失。此时模型输出为N维，标签为N维。

model.compile(...,
              loss=tf.keras.metrics.categorical_crossentropy,

              ...)

4 其他

“sparse_categorical_crossentropy ” 等同tf.keras.metrics.sparse_categorical_crossentropy

“categorical_crossentropy ” 等同tf.keras.metrics.categorical_crossentropy

...