本文参考
https://zhuanlan.zhihu.com/p/580458091
1、数字角频率ω与模拟角频率Ω的理解
我们之前的课程接触最多的是模拟频率f,包括在模拟电路、高频电路以及传感器课程上,都是以f作为频率响应函数的横坐标。使用f的好处是其真实反映了实际系统的工作情况,从0到∞,反映了实际模拟信号振荡速度的快慢。
模拟角频率Ω=2πf,过去我们常将ω作为模拟角频率,写成cos(ωt),这种写法实际上是不正确的,应该写成cos(Ωt)来描述模拟余弦函数。此时Ω的取值也是从0到∞,这体现出模拟(角)频率没有周期性的特点。
数字角频率ω则是完全颠覆了我们过往对于频率的认识,首先要明确的是数字信号的获得是通过对模拟信号采样的方式。它的引入可以从cos(Ωt)开始。cos(Ωt)中相位变化一个周期(2π)所需的时间为T,那么模拟角频率定义成Ω=2π/T。对于该余弦信号,采样之后变成了一个离散的数字序列,此时再谈论过了多少时间走完一个周期已经没有意义,而是过了间隔N相位刚好变化一个周期。因此数字角频率推导出为ω=2π/N,余弦信号则为cos(ωn)。既然N是由对应一段时间T采样而来,那么N=T*Fs (Fs为采样率),自然而然,ω=Ω/Fs。简单来说,数字角频率ω是模拟角频率Ω对于采样率Fs的归一化,这是数字角频率ω的核心要义。

2、巴特沃斯模拟滤波器的设计
巴特沃斯滤波器是一种常见的滤波器类型,它具有平坦的通带响应和陡峭的阻带衰减特性。巴特沃斯滤波器设计原理基于模拟滤波器的频率响应和极点分布。
巴特沃斯滤波器的设计目标是在通带范围内尽可能平坦地传递信号,并在阻带范围内实现最大的衰减。其频率响应特性是由极点位置和阶数(滤波器的阶数表示极点或零点的总数)来确定的。
巴特沃斯滤波器的特点是在通带内没有波纹,即在通过频率范围内的增益是均匀的。而阻带范围内的衰减是非常陡峭的,越高阶的巴特沃斯滤波器具有更陡峭的阻带衰减。
巴特沃斯滤波器的设计步骤如下:
(1)确定所需的滤波器类型(低通、高通、带通或带阻),以及通带和阻带的边界频率。
(2)将通带和阻带的频率范围转换为归一化频率,即将通带截止频率设置为1。
(3)根据滤波器的阶数选择适当的极点数量。每个极点都是一个复数,可以通过计算来确定其位置。
(4)根据极点的位置,构建滤波器的传递函数。对于巴特沃斯滤波器,传递函数可以表示为一个多项式的比值。
(5)根据所需的滤波器增益,对传递函数进行归一化或缩放。
(6)如果需要,将模拟滤波器的设计转换为数字滤波器的设计,可以使用数字滤波器设计方法(如脉冲响应、频率抽样等)。
注:数字信号处理第172页
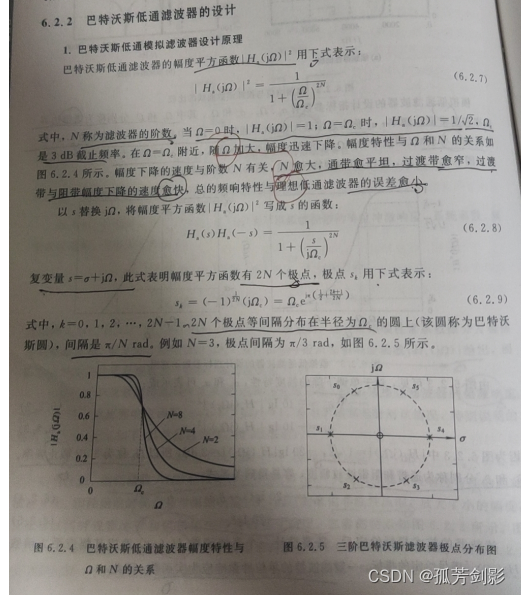



3、求取n阶低通模拟滤波器的极点

4、双线性变换
利用双线性变换可以将低通模拟滤波器转化为低通数字滤波器,进而获得滤波器的传递函数。
1 .预畸变(Prewarp)

2.双线性变换(Tustin变换)

5、低通转高通滤波器的处理

6、低通转带通滤波器的处理

7、低通转带阻滤波器的处理

8、计算滤波器的传递函数

9、计算增益
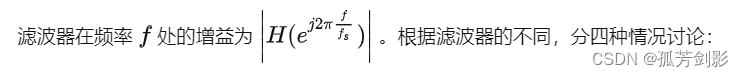
1.低通滤波器的增益

2.高通滤波器的增益

3.带通滤波器的增益

4.带阻滤波器的增益

10、计算IIR系数

11、数字滤波器的设计

12、一阶巴特沃斯低通,高通,带通滤波器的差分方程
1.一阶巴特沃斯低通滤波器差分方程:
差分方程形式为:
y[n] = (1 - c) * y[n-1] + c * x[n]
其中,y[n]表示当前时刻的输出信号,x[n]表示当前时刻的输入信号,c为滤波器的系数,它的取值范围为0到1。c越接近1,滤波器的截止频率越低。
2.一阶巴特沃斯高通滤波器差分方程:
差分方程形式为:
y[n] = c * y[n-1] + c * (x[n] - x[n-1])
其中,y[n]表示当前时刻的输出信号,x[n]表示当前时刻的输入信号,c为滤波器的系数,它的取值范围为0到1。c越接近1,滤波器的截止频率越高。
3.一阶巴特沃斯带通滤波器差分方程:
差分方程形式为:
y[n] = (1 - c) * y[n-1] + c * (x[n] - x[n-1])
其中,y[n]表示当前时刻的输出信号,x[n]表示当前时刻的输入信号,c为滤波器的系数,它的取值范围为0到1。c越接近1,滤波器的带通频率越窄。
13、一阶IIR滤波器的低通,高通,带通滤波器的差分方程
注:b0 和 b1 是前向系数,由 filterCoefficients->gain 决定
a1 是反馈系数,由 filterCoefficients->yc[0] 决定
1.低通滤波器:
差分方程:
y[n] = b0 * x[n] + b1 * x[n-1] - a1 * y[n-1]
其中,y[n]是输出信号,x[n]是输入信号,b0、b1是前向系数,a1是反馈系数。
2.高通滤波器:
差分方程:
y[n] = b0 * x[n] + b1 * x[n-1] - a1 * y[n-1]
与低通滤波器相比,高通滤波器的差分方程中的反馈系数a1取相反数,即a1 = -a1。
3.带通滤波器:
差分方程:
y[n] = b0 * x[n] + b1 * x[n-1] - a1 * y[n-1] - a2 * y[n-2]
14.滤波器的差分方程