二分图最大匹配

二分图是一种奇妙的图，它满足可以把其内部的节点划分成两个集合，且这每个集合内部的的点没有边相连。

二分图的判定

二分图的判定定理：一张无向图是二分图，当且仅当图中不存在奇环（长度为奇数的环）。

于是乎，对于二分图的判定，我们可以使用染色的方法。尝试用黑和白两种颜色标记图中的点，当一个节点被标记了，那么所有与它相连的点应全部标记为相反的颜色，如果在标记过程中出现颜色冲突，那么算法结束，图中存在奇环，不为二分图；否则，本图是二分图。

对于二分图的判定，还有一种利用并查集的判定方式，相较于染色法在时间复杂度上更优，但是我还不会诶/kk。

二分图最大匹配

匈牙利算法，是一种解决二分图最大匹配问题的算法。

知道了二分图是什么，我们还需要知道“匹配”是什么。我们称图 $G$ 的一个匹配是由一组没有公共端点的边的集合。最大匹配包含的边数即为最大匹配。

归纳一下，对于一个匹配有两点要求：

• 匹配是边的集合

• 在匹配中，任意两边不能有公共顶点

然后我们就可以开始解决二分图的最大匹配问题啦！

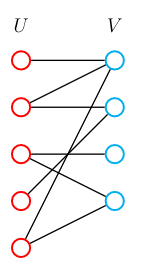
我们形象地描述一下这个问题，对于上面的二分图，$U$ 表示男生，$V$ 表示女生，两集合中点之间的边表示两人有暧昧关系，作为一名单身狗，你的目的是尽可能多地撮合情侣，这就是找最大匹配的过程。但是注意，如果一个人已经有了男/女朋友就不能在找别的了，这就是要满足“任意两边不能有公共顶点”。

下面模拟匈牙利算法的过程：

1. $U$ 中的第一个 $U_1$ 寻求匹配，发现只能到 $V_1$，所以这一对可以；
2. 再看 $U_2$，发现它可以到 $V_1$ 和 $V_2$，但是 $V_1$ 已经有男朋友了，虽然 $U_2$ 是海王但是它不会抢别人的女友，并且 $U_1$ 只能和 $V_1$ 在一起，所以 $U_2$ 只好去找 $V_2$ 了；
3. 再看 $U_3$，发现它可以到 $V_3$ 和 $V_4$，这两个人都没有男朋友，所以先假设 $U_3$ 和 $V_3$ 在一起了。
4. 再看 $U_4$，发现它只能到 $V_2$，可是 $V_2$ 已经名花有主了，考虑让 $U_2$ 换一个目标，但是 $U_2$ 的另一个暧昧对象已经给 $U_1$，根据“先来后到”原则，$U_4$ 就和我们一样注定单身了；
5. 最后看 $U_5$，可以到 $V_1$ 和 $V_5$，$V_5$ 刚好没有男朋友，所以 $U_5$ 就开开心心地抱得美人归了。

时间复杂度 $O(VE)$。

---

具体代码实现如下：

#include <bits/stdc++.h>
using namespace std;

const int maxn=5e4+5;
int head[maxn],nxt[maxn],to[maxn],vis[maxn],cnt,match[505]/*表示右边点对应左边的cp*/,m,n,e;

void add(int x,int y)
{
	to[++cnt]=y;
	nxt[cnt]=head[x];
	head[x]=cnt;
}

bool dfs(int now)//找对象
{
	for(int i=head[now];i;i=nxt[i])
	{
		if(vis[to[i]]) continue;
		vis[to[i]]=1;
		if(!match[to[i]]||dfs(match[to[i]]))//想找的对象没有男朋友或者这个对象的当前男朋友还可以找别的女朋友
		{
			match[to[i]]=now;//左侧元素和当前的右侧元素形成匹配
			return 1;
		}
	}
	return 0;
}

int main()
{
	cin>>n>>m>>e;
	for(int i=1;i<=e;i++) 
	{
		int u,v;cin>>u>>v;
		add(u,v);
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		memset(vis,0,sizeof(vis));
		if(dfs(i)) ans++;
	}
	cout<<ans;
	return 0;
}