2019年亚太杯APMCM数学建模大赛
A题 基于图像分析的二氧化硅熔化表示模型
原题再现
铁尾矿的主要成分是二氧化硅,而二氧化硅是铁尾矿成分中最难熔化的部分。因此,铁尾矿的熔融行为可以用二氧化硅的熔融行为来表示。然而,高温熔池的温度超过1500,其中常规检测设备在环境下的使用寿命很短。为了解决这一问题,相关课题组在国内外首次采用了一种具有放大效果的CCD视频拍摄系统。该小组以非接触的方式获得了高温熔池中二氧化硅的动态可视化数据(时序下的序列图像),并通过视频分析观察了时序中二氧化硅的实时熔融速率,为渣棉制备过程中的尾矿添加和热补偿提供了指导,从而间接改进了高炉矿渣直接纤维成型技术。
二氧化硅在高温熔池中熔化过程中的时序图像(见附件,共114张图像;文件名称序号为时序,每隔1s采集一张图像)。采用的实验设备情况如下图所示:
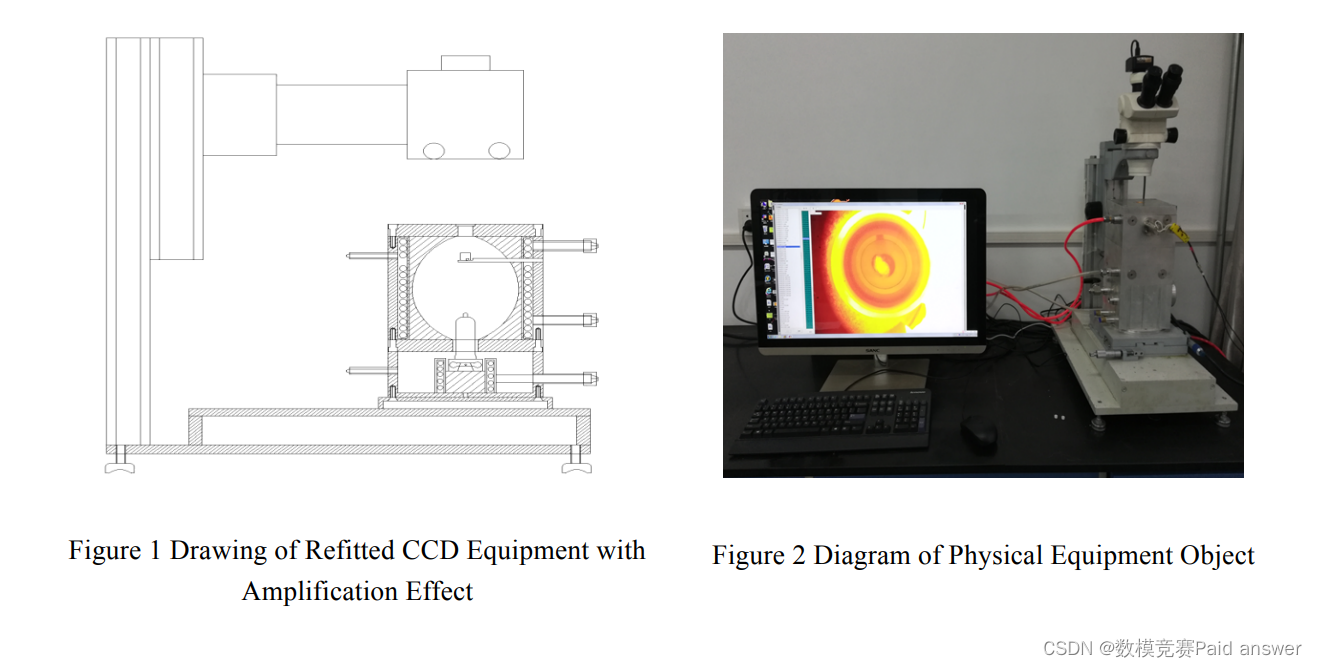
为了揭示铁尾矿在高炉矿渣中的溶解行为,采用铁尾矿的主要成分SiO2进行研究,研究了SiO2颗粒在高温下的熔融过程,以表征铁尾矿的熔融。试验准备的材料分别为:用于分析的纯SiO2颗粒(见图3)和直径为8mm的刚玉坩埚(见图4):

附件数字图像中显示的信息包括:
(1) 坩埚在图像中的固定位置;
(2) 未熔融的SiO2颗粒的位置可以随着时间序列而改变。
需要对附件中的图像进行以下分析
1.在熔化过程中,二氧化硅颗粒在高温熔池中的位置不断变化,分析二氧化硅熔化行为的第一步是跟踪目标。请建立一个数学模型来跟踪二氧化硅颗粒在熔化过程中的质心位置,并给出二氧化硅质心的运动轨迹。
2.建立表征二氧化硅熔融过程中二氧化硅边缘轮廓特征的指标(如形状、周长、面积、广义半径等);参与者可以自己选择,只要他们能代表二氧化硅的熔化过程。
3.对于附件中给出的图像是2D,而代表二氧化硅熔化速率的关键参数是质量,并且质量与3D体积成正比,根据第2题中二氧化硅的边缘轮廓特征指数来估计二氧化硅的实际熔化速率。
整体求解过程概述(摘要)
本文旨在模拟一种二氧化硅的熔化规律,这种熔化规律不能通过直接接触手段测量,只能通过图像监测手段间接测量。本文利用图像处理技术实现了二氧化硅熔融规律的测定。
在问题1中,我们建立了一个基于K-means算法的图像分割模型,利用这种成熟的聚类算法实现对原始图像信息的有效分割,从原始图像中提取二氧化硅的轮廓信息,同时利用Canny滤波技术去除图像轮廓周围的噪声,利用腐蚀和膨胀技术对有效轮廓区域进行细化,通过调整得到二氧化硅轮廓特征明显的二值图像。此外,建立图像所在平面的二维坐标系,并通过使用快速搜索算法确定二氧化硅区域在二值图像中的质心位置。最后,对114幅图像中二氧化硅的质心坐标进行计数,得到质心位置与离散时间点之间的关系,然后用该性质的高幂函数拟合函数曲线来满足二氧化硅中心的运动。通过残差函数的误差分析,拟合结果表明,二氧化硅质心的运动方程倾向于10次方函数。
在问题2中,我们选择面积指数作为二氧化硅熔融过程中的特征量,并且通过图像处理技术,在图像区域中只保留坩埚的横截面图像和二氧化硅的轮廓图像。此外,利用MATLAB软件的图像处理功能对两种轮廓线包围的所有像素进行计数。考虑到两个区域中像素总数的比率是两个区域的面积比率,并且坩埚的截面积是一定的值,我们将两个区域中像素总数的比率与它们的面积比率相关联,从而确定单位时间内二氧化硅剖面的面积。最后,对114幅图中二氧化硅剖面的面积数据进行了统计,得到了二氧化硅剖面面积与离散时间点之间的关系。利用MATLAB中的函数拟合工具箱对二氧化硅的熔融过程进行拟合,并对拟合结果进行误差分析。拟合结果表明,二氧化硅的熔融随时间的变化规律趋于3次方函数。
在问题3中,我们从一个新的想法出发,使用边缘滤波技术对原始平面二值图像进行两次滤波。这种滤波的目的是挖掘二值图像中过去没有检测到的空间区域,得到二氧化硅立体图像表面的隐藏沟壑区域,间接起到挖掘图像表面第三坐标的作用。经过去噪和目标提取,得到了一个新的具有第三坐标信息的二值二维图像。此外,通过像素数量和可测量量之间的比例来估计每个图像中二氧化硅的体积,从而获得体积和离散时间点之间的关系。此外,对二氧化硅的熔融过程进行了函数拟合。拟合结果表明,二氧化硅随时间的熔化规律更倾向于一种二次幂函数,而熔化速率与时间则倾向于线性关系,这与一些文献的结论基本一致。
模型假设:
① 假设成像环境的照明因子在每个时间间隔内是稳定的,并且光源的位置是固定的;
② 忽略一小部分二氧化硅的分离,因为在熔融过程中温度较高,只研究二氧化硅的主要部分;
③ 假设坩埚的横截面是一个标准圆;
④ 假设二氧化硅的密度是均匀分布的;
⑤ 由于二氧化硅的质量与其体积成正比,我们假设二氧化硅颗粒的密度为第一单元,并进一步将熔化过程中的质量与时间的关系变为体积与时间的联系。
问题分析:
问题分析1
对于问题1,为了建立二氧化硅熔化过程中质心的位移和运动轨迹模型,首先要根据CCD视频拍摄系统获得的114幅连续的二氧化硅熔化图像,在1秒内确定二氧化硅质心在图像平面(2D)上的坐标。由于图像整个平面的位置是固定的,因此如果每秒可以确定二氧化硅质心在整个图像平面中的位置,则意味着可以进一步确定质心在114秒内的位置分布特征。因此,我们可以得到质心位置与离散时间点之间的关系,然后通过适当的数值拟合,我们可以进一步得到满足二氧化硅质心运动特性的函数曲线。
问题分析2
对于问题2,我们分析了CCD相机获取的二氧化硅轮廓的第一个特征是其轮廓面积,因此我们应该选择面积因子作为描述二氧化硅熔化过程中边缘轮廓特征的指标。首先,我们应该使用图像处理技术来去除整个图像的黑色背景,此时图像区域只保留坩埚截面的图像和二氧化硅的轮廓图像。然后,我们应该使用MATLAB中的图像处理函数来计算这两种轮廓线所包围的所有像素。可以认为,两个像素的比率是两者的面积比率,因此我们可以进一步将两个像素与面积比率相关联,因此,二氧化硅轮廓的面积可以每秒确定。根据提取的面积信息,我们还应该使用MATLAB中的函数拟合工具箱来拟合二氧化硅的熔化过程。
问题分析3
对于问题3,根据问题3的信息,可以看出,表示二氧化硅熔融速率的基本参数是二氧化硅的质量,而不是二氧化硅的二维面积,因此有必要在二氧化硅的熔融过程中找到质量和时间之间的关系,并且由于体积是一个三维参数,因此需要重建原始的二维图像。通常,2D图像的3D重建过程是指重建2D灰度图像表面的3D形状的操作,在这个重建过程中使用的算法通常是SFS和SFX,但经过我们的分析,这些算法对前景背景灰度差、图像亮度和分辨率都有很高的要求,即,它们需要具有高分辨率和与背景颜色差异大的灰度图像。然而,数据提供的114幅图像中的大多数都不能满足这种要求。即使进行图像增强预处理操作,也不能保证大多数图像的前景和背景灰度的差异能够满足三维重建的要求。因此,我们应该重新利用图像处理技术来提取二维图像中的三维特征信息,我们应该尝试挖掘二维二值图像中未检测到的空间区域。
模型的建立与求解整体论文缩略图



全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
clc;
clear;
A=imread('E:\ACMC\2019 APMCM Problems\2019 APMCM Problem A
Attachment\c\0606.bmp');%读取原图像
As=imread('E:\ACMC\2019 APMCM Problems\2019 APMCM Problem A
Attachment\b\0571.bmp');%读取原图像
% [filename,pathname]=uigetfile({'*.jpg';'*bmp';'*gif'},'E:\ACMC\2019 APMCM
Problems\2019 APMCM Problem A Attachment\0497.bmp');
% I = imread([pathname,filename]);
% I = A;
% B=A;
I=rgb2gray(A);%将原图像转换为灰度图像
B=rgb2gray(A);%将原图像转换为灰度图像
t=graythresh(B);%计算阈值 tv
C=im2bw(B,t);%根据阈值二值化图像
C1=im2bw(B,0.7298);%根据阈值二值化图像 8198 77
D=imfill(C,8,'holes');%对二值化后的图像填充肺实质
E=D-C;%得到肺实质的图像 E
F=imfill(E,8,'holes');%填充肺实质空洞
B=double(B); %%%%%%%%%%%%%%%注意这个地方,必须换成 double 类
型
BW5=edge(I,'Canny',0.035);%0.037 %a 0.035
% subplot(2,3,6);
% imshow(BW5);
%title('Canny 算子边缘检测')
G=B.*D;
H=BW5+G;
%figure,imshow(A);
%figure,imshow(G);
%figure,imshow(H);
%figure,imshow(~C1);
F=(C1)+(~G);
%figure,imshow(F);
K=(F)+BW5;
figure,imshow(BW5);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%
%形态学腐蚀膨胀处理
se=strel('square',10');%方型结构元素
se1=strel('square',3');%方型结构元素
se2=strel('square',3');%方型结构元素
% A2=imdilate(A1,se);%腐蚀
% B1=imerode(A2,se);%膨胀
% A3=imdilate(B1,se1);%腐蚀
% B2=imerode(A3,se1);%膨胀
% B2 = bwmorph(A1,'close'); %运算
% B3 = bwmorph(B2,'close'); %运算
% B4 = bwmorph(B3,'close'); %运算
% B5 = bwmorph(B4,'close'); %运算
% %figure,imshow(B5);
% p1=imdilate(BW5,se);%腐蚀
BW5=imdilate(BW5,se);%膨胀
figure,imshow(BW5);
% figure,imshow(p2);
%目标选择
[M,N]=size(BW5);
buffer = F;
%figure,imshow(K);
size = 80;
for i=2:M-1
for j=2:N-1
% if((i>=(256-size) && i<=(256+size))&&(j>=(1005-size) &&
j<=(1005+size)))
% if((i>=(406-size) && i<=(496+size))&&(j>=( 655-size) &&
j<=(675+size)))
if((i>=(306-size) && i<=(246+size))&&(j>=(955-size) &&
j<=(1055+size)))
buffer(i,j)=BW5(i,j);
else
buffer(i,j)=0;
end
end
end
A1 = K;
figure;
buffer=imfill(buffer,8,'holes');%填充肺实质空洞
imshow(buffer);
%计算坐标
coorx = 0;
coory = 0;
cnt = 0;
for i=2:M-1
for j=2:N-1
if(buffer(i,j) == 1)
coorx = coorx + i;
coory = coory + j;
cnt = cnt + 1;
end
end
end
coor_x = coorx/cnt;
coor_y = coory/cnt;
coor = [coor_x,coor_y];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%
%形态学腐蚀膨胀处理
se=strel('square',5');%方型结构元素
se1=strel('square',3');%方型结构元素
se2=strel('square',3');%方型结构元素
zhongxin = [1052,583];
%figure,imshow(C1);
% [zhongxin,banjin,gongzhi] = imfindcircles(C1,[1,2000]);
viscircles(zhongxin, 528,'EdgeColor','b');
S_cir = pi * 528^2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%
%面积比例计算
Scnt = 0;
for i=2:M-1
for j=2:N-1
if((i-1052)^2+(j-583)^2 <=528^2)
Scnt = Scnt + 1;
end
end
end
pic_bili = cnt/Scnt;