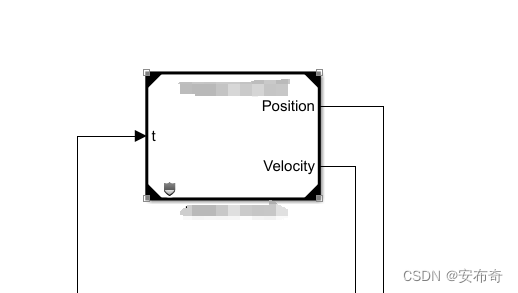
f i = min ( a j − j × i ) f_i=\min(a_j - j \times i) fi=min(aj−j×i)
考虑变成点对 ( j , a j ) (j,a_j) (j,aj),则 f i = Y j − X j i f_i=Y_j-X_ji fi=Yj−Xji
令 i = k , f i = b i=k, f_i=b i=k,fi=b,得 b = Y j − X j k b=Y_j-X_jk b=Yj−Xjk,即 Y j = X j k + b Y_j=X_jk+b Yj=Xjk+b
我们希望 b b b 尽量小,也就是截距尽可能小,即下图红色部分
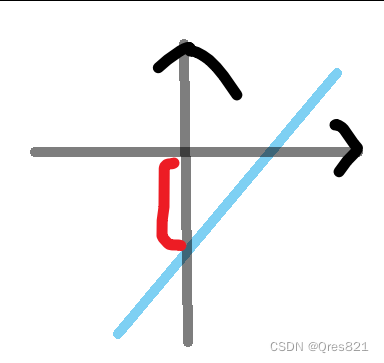
对于点对,我们维护凸壳
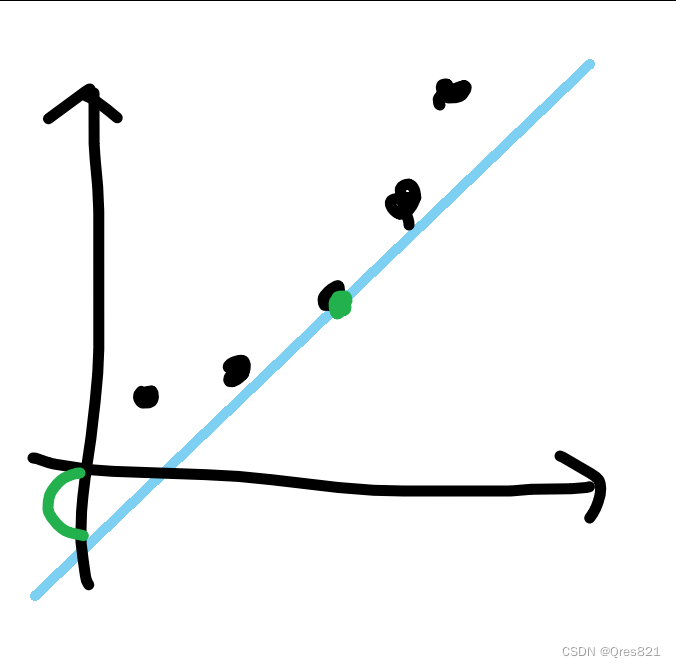
可以发现,在第一个切的地方我们可以取截距最小
维护凸壳采用的是单调队列,我们维护两点之间斜率递增
如果新加入的点会使斜率递减,则把队尾的点pop掉
然后我们就可以二分 / 决策单调性了